2022年五一杯数学建模
C题 火灾报警系统问题
原题再现:
二十世纪90年代以来,我国火灾探测报警产业化发展非常迅猛,从事火灾探测报警产品生产的企业已超过100家,年产值达几十亿元,已经成为我国高新技术产业的一个组成部分,国外产品也大量进入我国市场。我国每年建筑中新安装的火灾探测器约200万只。
火灾探测器的功能就是捕捉特定的火灾信号,将其转换为电信号传输至火灾报警控制器依据报警算法进行判定,当探测到的信号数值或者变化特征超过阈值时即被判定为火灾。因此探测器的灵敏度决定了对火灾特征响应的灵敏程度,但较高的灵敏度会导致报警可靠性的降低,而较高的可靠性则需要牺牲探测器的灵敏度。因此,探测器的灵敏度和可靠性成为探测器需要平衡考虑的关键参数 (有关火灾报警系统的其他相关背景资料见附件4:火灾报警系统背景资料)。
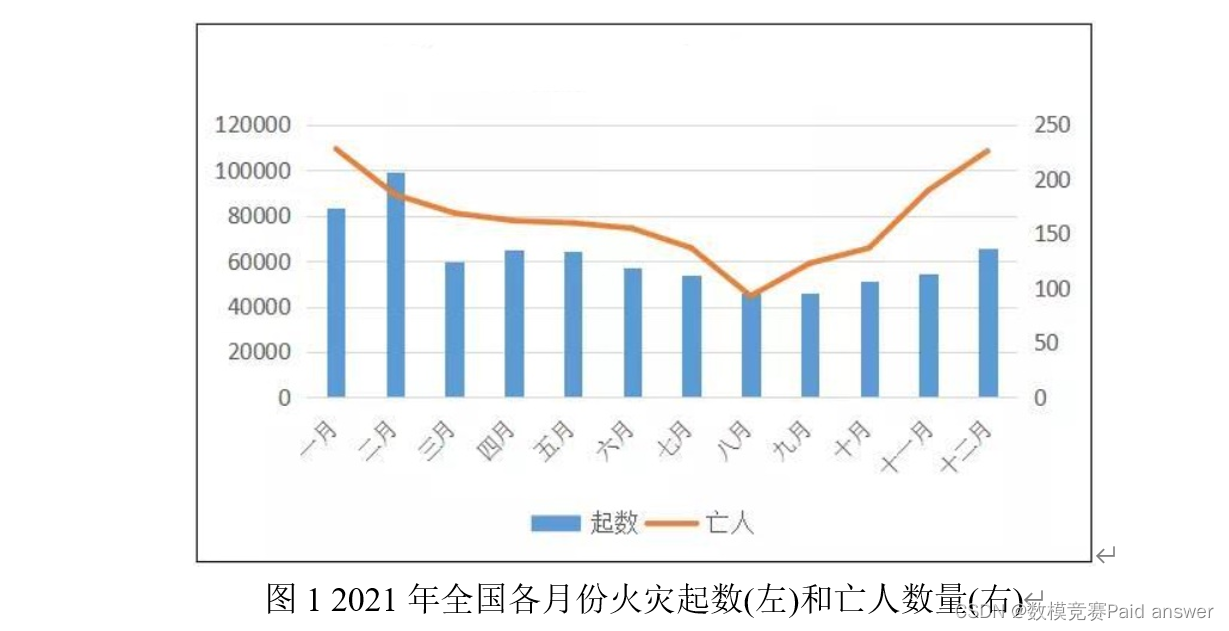
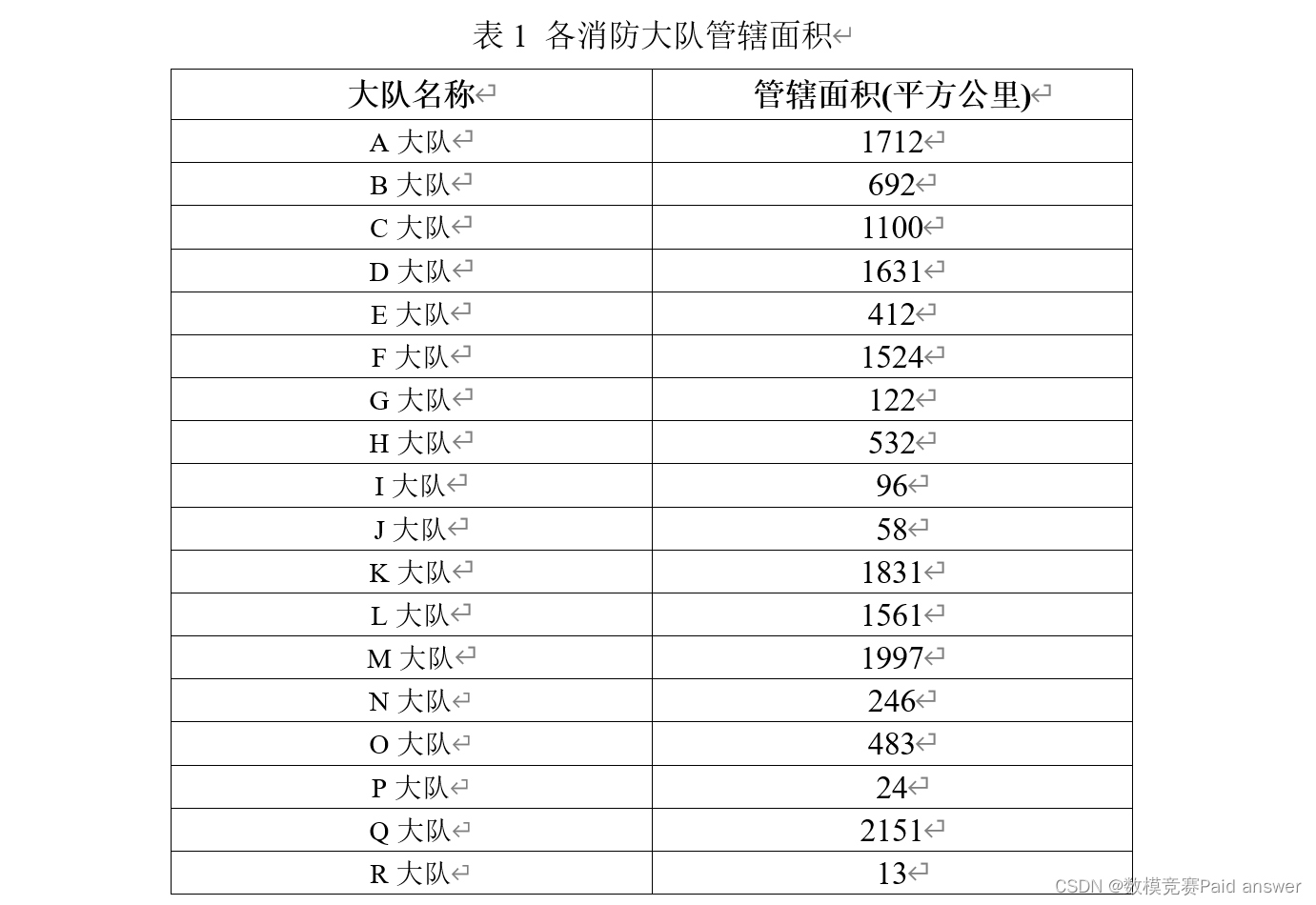
图1为全国2021年各月份的火灾次数及变化趋势,假设我国某城市一年内的火灾起数的变化趋势与全国2021年各月份的火灾次数及变化趋势相似,该城市在(6月1日至6月18日)18天内共接到257179条火灾报警系统的报警信息(其中包含误动作所导致的误报警),附件1是该城市6月1日至6月18日统计的火灾报警数据;该城市共有18个消防大队,管辖面积如表1所示;除了误动作以外,该城市中还有一部分火灾报警系统存在故障问题如附件2所示。假设正常工作的火灾探测器检测到火灾时一定会报警,忽略时间的影响,当某一建筑内多个火灾探测器的机号与回路编号相同时且这些探测器均发出火灾报警信号,则认为是同一起火灾事故。
在探测器安装得当,符合标准的假设下,讨论如下问题:
问题1:请根据文中叙述及附件1,确定该城市6月1日至6月18日的真实火灾起数,并查阅参考文献,结合附件2、图1(附件2中部分部件无需分析,请依据附件1的部件名称先对附件2的部件进行模型筛选),通过建立模型对附件1中的各类型部件进行分析,利用可靠性和故障率对各类型部件进行评价,帮助政府选取更加可靠的火灾探测器类型。
问题2:通过阅读参考文献,结合问题1得到的数据结论,选择合适参数建立区域报警部件类型智能研判模型,当某大队辖区内某类型部件发出报警信息时,能够较好判断是否属于误报,提高报警准确率,并对附件3中各大队不同部件发出的报警信号进行真实性评价,确定附件3中各报警信号是真实火灾的概率。
问题3:根据问题1所获得的各辖区火灾数据以及问题2的结果,结合表1分析该市各消防大队的综合管理水平,并将综合管理水平最低的三个辖区的技术指标(如辖区火灾发生频率、部件故障率、部件可靠性等)进行量化,提出改进方案。
问题4:根据有关文献和问题1至问题3模型分析的结果,请有针对的提出火灾报警系统各部件管理维护的意见建议。
整体求解过程概述(摘要)
本文针对火灾报警系统问题,建立熵权-TOPSIS、回归等数学模型,旨在通过所建模型来选取可靠的探测器、提高报警准确率及改进各辖区综合管理水平,从而减少我国火灾事故。
针对问题一,首先根据地址、机号和回路,确定真实火灾数为418起。接着根据题目要求,基于可靠性和故障率两个指标建立综合评价模型。由于可靠性为效益型指标,而故障率为成本型指标,故将故障率通过数学公式转换为效益型指标,即完善率。指标确定后,运用熵权法确定各指标权重,最后利用TOPSIS法构建各类型部件评价模型,对16种部件进行综合评价,帮助政府选择最可靠的5种火灾探测器类型,分别为光束感烟、手动报警按钮、智能光电探头、点型感温探测器、线性光束感烟探测器。
针对问题二,建立基于Logistic回归的区域报警部件类型智能研判模型。本文选择故障次数、消防大队及探测器类型3个变量作为自变量,误报与否作为因变量,将消防大队和探测器类型两个无序分类变量变为虚拟变量,利用Logistic回归模型预测辖区内某类型部件发出报警信息正确的概率,经检验模型的真实性为94.7%,附件三中各个大队各个不同类型的报警器的报警信号是真实火警的概率依次为如下结果:19.3%,0.8%,1.01%,2.6%,98.67%,0.55%,7.02%,75.23%,0.85%,11.2%,71.2%,79.06%,7.9%,54.67%,19.38%经检验结果有所偏差,故进行模型优化用WOE值代替原值计算,使得结果更加真实可靠。
针对问题三,根据题目要求,本文选取单位面积火灾发生概率、单位面积火灾报警数、误报率及故障率作为评价指标,运用熵权法确定各指标权重,再利用TOPSIS法构建各消防大队评价模型,根据求解的综合得分得出管理水平最低的三个大队是J、G、I,接着将以上三个大队的各指标数字与所有消防大队的指标均值进行对比,从而提出一些针对性建议。
针对问题四,根据搜查相关文献和前三问模型分析的结果,从触发装置、报警装置检查、电源检查等相关火灾报警系统及技术档案资料管理有针对的提出管理维护的建议,从而降低火灾率及误报警率,完善火灾报警系统。
模型假设:
1. 假设各大队的管辖面积大小不影响区域报警部件类型的选取;
2. 假设正常工作的火灾探测器检测到火灾时一定会报警;
3. 假设多个火灾探测器地址、机号和回路编号相同时且都发出火灾报警信号,则认为是同一场火灾。
4. 假设未考虑的次要因素对综合管理水平影响不大。
问题分析:
针对问题一,本文建立熵权法-TOPSIS模型。首先通过Excel处理附件一数据得到该城市6月1日到18日的真实火灾起数。然后整理附件一和附件二的数据,得到各类部件的可靠性和故障率,将故障率利用数学公式处理为完善率。接着基于可靠性和完善率两个指标,构建熵权法–TOPSIS模型从而对各类部件进行综合评价,在最终评价结果出选取更可靠的火灾探测器类型。
针对问题二,题目求结合问题1得到的数据结论,选择合适的参数,建立区域报警部件类型智能研判模型,并评价附件3中各大队不同部件发出的报警信号的真实性,确定各报警信号是真实火灾的概率。本文拟通过所在区域、部件类型和其他信息来选择合适的参数,然后建立Logistic回归模型来预测各部件报警正确的概率,利用该模型,评价附件3中各大队不同部件发出的报警信号的真实性,确定各报警信号是真实火灾的概率。检验模型如模型结果偏差过大进行模型优化。
针对问题三,题目要求对辖区的技术指标进行量化,对该市各消防大队的综合管理水平进行评价并针对管理水平最低的三个消防大队提出改进方案。本文首先根据问题一问题二提供的评价指标,从单位面积火灾发生概率、单位面积火灾报警数、误报率及故障率四个评价指标对各消防大队的综合管理水平进行评价。接着运用熵权法求出各指标的权重,再建立TOPSIS模型对各消防大队的综合水平进行评价,求出各个消防大队的评价得分;最终根据所求数据对综合管理水平最低的三个辖区提出改进方案。
针对问题四,本文根据相关文献和问题一至问题三所得结果,总结分析并给出针对火灾报警部件及档案资料管理的建议,以提高火灾报警系统的准确性。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
部分程序如下:
% 第一列为可靠性,第二列为故障率
Q_2 = [];
% 对故障率进行正向化
MAX = max(Q_2);
Q_2_M = Q_2(:,1);
for i = 1:length(Q_2)
Q_2_M(i,2) = abs(MAX(2)-Q_2(i,2));
end
% 标准化处理
MIN = min(Q_2_M);
MAX = max(Q_2_M);
Q_2_MIAX = [];
for i = 1:length(Q_2)
Q_2_MIAX(i,1) = (Q_2_M(i,1)-MIN(1))/(MAX(1) - MIN(1));
Q_2_MIAX(i,2) = (Q_2_M(i,2)-MIN(2))/(MAX(2) - MIN(2));
end
% 熵权法
Z = Q_2_MIAX;
[n,m] = size(Z);
D = zeros(1,m); % 初始化保存信息效用值的行向量
for i = 1:m
x = Z(:,i); % 取出第i列的指标
p = x / sum(x);
% 注意,p有可能为0,此时计算ln(p)*p时,Matlab会返回NaN,所以要判断
n = length(p); % 向量的长度
lnp = zeros(n,1); % 初始化最后的结果
for j = 1:n % 开始循环
if p(j) == 0 % 如果第i个元素为0
lnp(j) = 0; % 那么返回的第i个结果也为0
else
lnp(j) = log(p(j));
end
end
%到这里结束
e = -sum(p .* lnp) / log(n); % 计算信息熵
D(i) = 1- e; % 计算信息效用值
end
W = D ./ sum(D); % 将信息效用值归一化,得到权重
W
% TOPSIS
D_min = min(Q_2_MIAX);
D_max = max(Q_2_MIAX);
zonghedefen = 1:13; %生成记录点
for i = 1:13
%利用(C = D-/((D-)+(D+)))topsis模型与熵权进行结合
D_jia = sqrt(W(1)*(Q_2_MIAX(i,1)-D_max(1))^2+W(2)*(Q_2_MIAX(i,2)-D_max(2))^2);
D_jian = sqrt(W(1)*(Q_2_MIAX(i,1)-D_min(1))^2+W(2)*(Q_2_MIAX(i,2)-D_min(2))^2);
zonghedefen(i) = D_jian/(D_jia+D_jian);
end
zonghedefen = zonghedefen'