一、运行结果；

二、源代码；

# define _CRT_SECURE_NO_WARNINGS
# include <stdio.h>

int main()
{
	//初始化变量值；
	int remainder = 1;
	int m = 0;
	int n = 0;
	int middle = 0;

	//提示用户；
	printf("请输入整数m和n的值：");

	//获取用户输入的数值；
	scanf("%d %d", &m, &n);

	//判断m和n的大小；
	if (m > n)
	{
		//不做改变；
	}
	else
	{
		//交换m和n的值；
		middle = m;
		m = n;
		n = middle;
	}

	//求最大公约数；
	while (remainder != 0)
	{
		//运算；
		remainder = m % n;

		//交换数值；
		m = n;
		n = remainder;

	}

	//输出结果;
	printf("最大公约数为：%d", m, n, n);

	return 0;
}

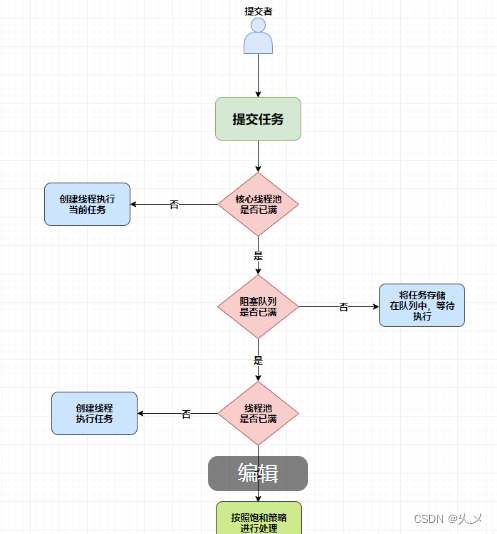
三、流程图；

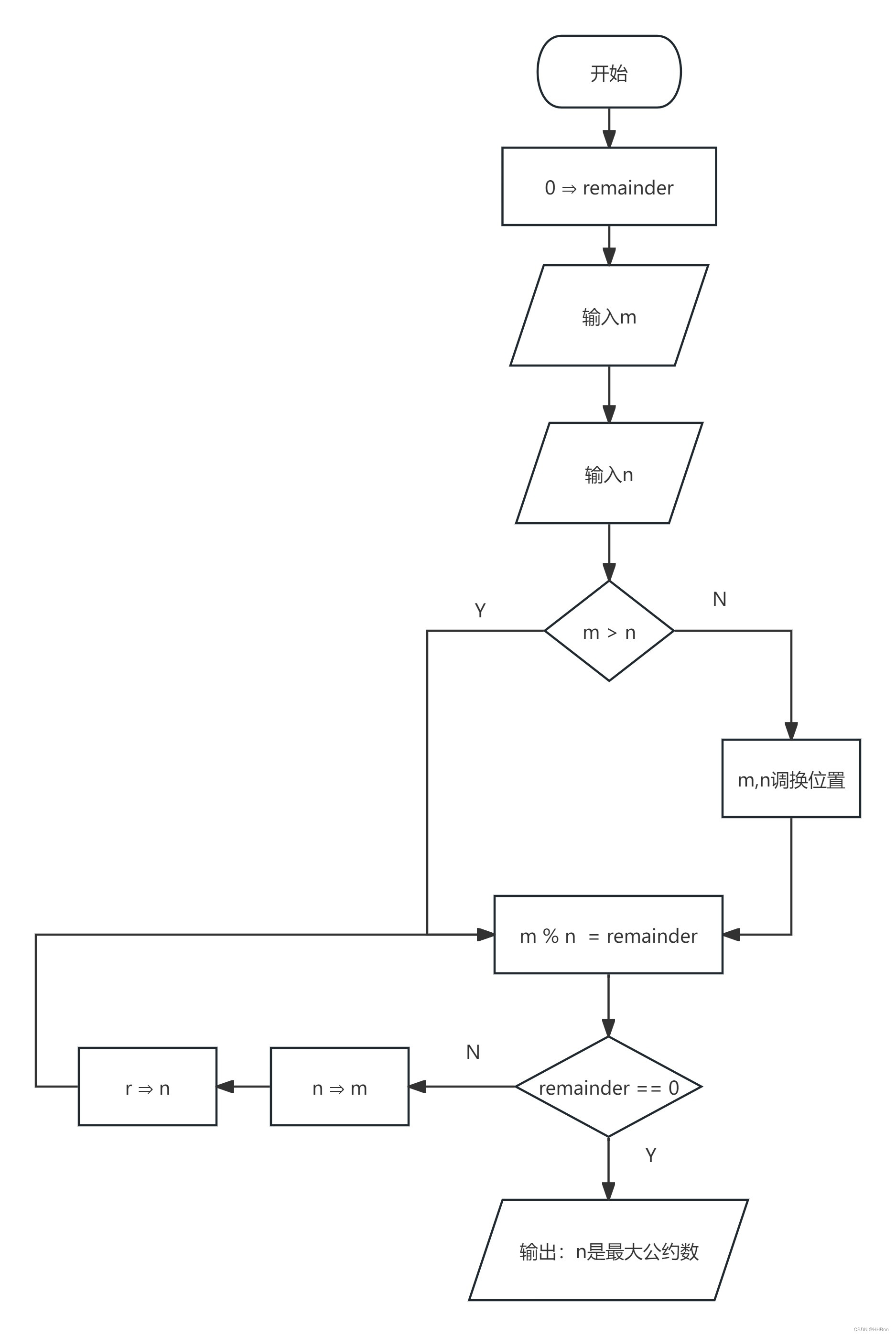
四、N-S流程图；