堆排序
讲堆排序之前我们需要了解几个定义
什么叫做最大堆,父亲节点,以及孩子节点
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
每个节点都是它的子树的根节点的父亲 。 反过来每个节点都是它父亲的孩子 。
下面讲一下思路:
第一步我们将待排序数组调整成最大堆的形式:父亲节点大于孩子节点(堆结构,父亲节点的下标为i,左孩子节点的下标为2*i+1,右孩子的节点下标为2*i+2)
第二步:我们将堆顶元素与待排序数组最后一个元素发生交换
第三步:待排序数组数据量减少一个,继续调整成最大堆形式。
代码如下
adjust函数
void adjust(int* nums, int start, int end) {
int father = start;
int child = 2 * father + 1;
while (child <= end) {
if ((child + 1) <= end && nums[child] < nums[child + 1]) {
child++;
}
if (nums[child] > nums[father]) {
swap(&nums[child], &nums[father]);
father = child;
child = 2 * father + 1;
}
else {
break;//调整防止死循环
}
}
}
堆函数
void heapsort(int* nums, int n) {
//初始化堆(形成最大堆)
//从最后一个父亲节点开始n/2-1;
//一直调整到父亲节点为0;
for (int i = n / 2 - 1; i >= 0; i--) {
adjust(nums, i, n - 1);//i是父亲节点下标,n-1是最后一个元素
}
//堆顶与待排最后一个元素交换
for (int j = n - 1; j >= 1; j--) {
swap(&nums[0], &nums[j]);
adjust(nums, 0, j - 1);
}
}
时间复杂度:O(nlogn),不稳定。
快速排序
在讲快排之前我们引入三色旗问题

解题思路:
第一步定义两个变量 i=start-1,j=end+1,从index=0的位置开始遍历。
分析

如果后边的元素比基准值大,那么我们不需要交换,只需要将遍历数组的下标index++既可,如果后边的元素比基准值小的话,我们需要交换元素的位置,基准值前边的我们都遍历过了所以不用再依次比较了
思考一下将三色旗问题引入到快速排序算法中呢,
我们需要确定一个基准值,暂且将待排序数组的一个元素设置为基准值。
第二步找到比基准值大,比基准值小的元素,将待排序数组分成三部分。一个比基准值小的数组,基准值,比基准值大的数组。进行进行分区处理。利用递归的思想。
代码如下
void quicksort(int*nums,int start,int end){
if(start>=end)return;
int i=start-1;
int j=end+1;
int index=start;
int temp=nums[start];
while(index<j){
if(nums[index]<temp){
swap(&nums[++i],&nums[index]);
}else if(nums[index]>temp){
swap(&nums[--j],&nums[index]);
}else{
index++;
}
}
quicksort(nums,start,i);
quicksort(nums,j,end);
}时间复杂度:

最好的情况为O(nlogn),最糟糕情况O(n^2);
稳定性:不稳定的。
归并排序
归并排序是用分治思想,三个步骤:
- 分解(Divide):将n个元素分成个含n/2个元素的子序列。
- 解决(Conquer):用合并排序法对两个子序列递归的排序。
- 合并(Combine):合并两个已排序的子序列已得到排序结果。
将两个有序数组合并成一个有序数组
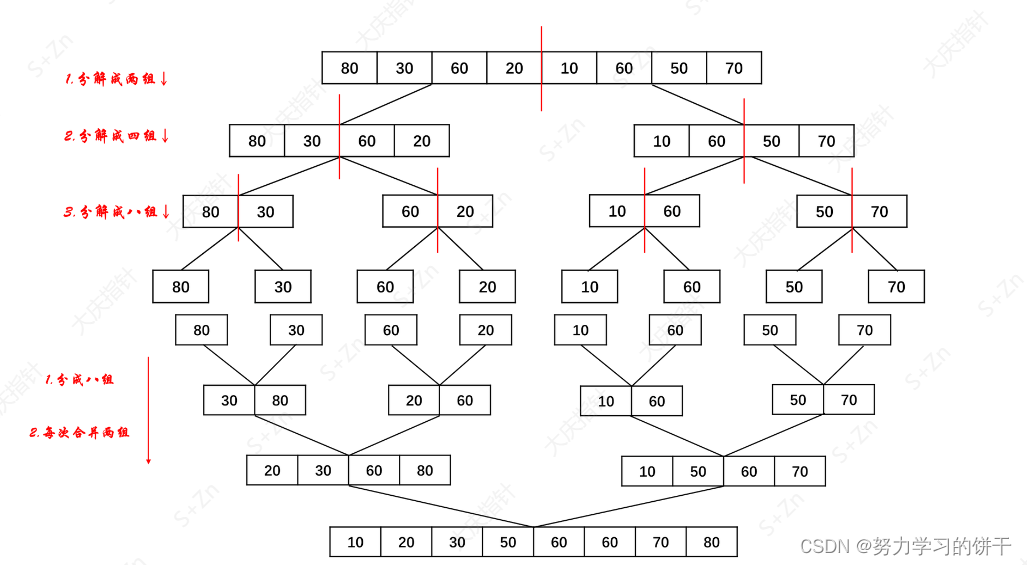
写一下代码
//归并排序
void merge(int*nums,int left,int mid,int right){
int *temp=(int*)malloc(sizeof(int)*(right-left+1));
int i=left;
int j=mid+1;
int index=0;
while(i<=mid&&j<=right){
if(nums[i]<=nums[j]){
temp[index++]=nums[i++];
}else{
temp[index++]=nums[j++];
}
}
while(i<=mid){
temp[index++]=nums[i++];
}
while(j<=right){
temp[index++]=nums[j++];
}
index=0;
for(int i=left;i<right;i++){
nums[i]=temp[index++];
}
free(temp);
}
void merg(int*nums,int left,int right){
if(left>=right)return;
int mid=(right-left)/2+left;
merg(nums,left,mid);
merg(nums,mid+1,right);
merge(nums.left,mid,right);
}归并排序的时间复杂度:最好的情况:O(nlogn),

最坏的时候O(n^2)
稳定