二叉树进阶——手撕二叉搜索树

news2024/11/20 0:30:23

troop主页：troop

手撕二叉搜索树

  • 1.二叉搜索树的定义
  • 2.实现（非递归）
    • 补充结构
    • 2.1查找
    • 2.2插入
    • 2.3删除（==重要==）
      • 情况1(无孩子&&一个孩子）
  • 3.二叉搜索树的应用
    • 3.1K模型
    • 3.2KV模型
      • 3.2.1KV模型的实现
  • 总结
  • 二叉搜索树源代码

1.二叉搜索树的定义

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树：

  • 若它的左子树不为空，则左子树上的所有节点的值都小于根节点的值
  • 若它的右子树不为空，则右子树上的所有节点的值都大于根节点的值

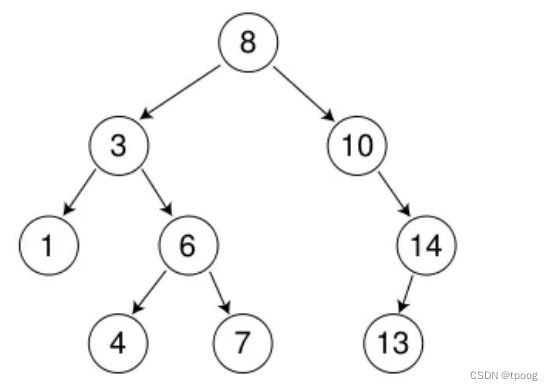
在这里插入图片描述

2.实现（非递归）

补充结构

//struct BinarySearchTreeNode
template<class K>
struct BSTreeNode
{
	typedef BSTreeNode<K> Node;
	Node* _left;
	Node* _right;
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{}
};

/class BinarySearchTree
template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
	BSTree() = default;
	BSTree(const BSTree<K>& t)
	{
		_root = copy(t._root);
	}
	Node* copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;
		Node* newroot = new Node(root->_val);
		newroot->_left = copy(root->_left);
		newroot->_right = copy(root->_right);
		return newroot;
	}

	~BSTree()
	{
		Destroy();
	}
	void Destroy()
	{
		return _Destroy(_root);
	}
	void _Destroy(Node* root)
	{
		if (root == nullptr)
			return;
		_Destroy(root->_left);
		_Destroy(root->_right);
		delete root;
	}
private:
	Node* _root;
};

2.1查找

根据它的定义查找就是，跟节点比，比节点大就去它的右子树中寻找，比他小就去它的左子树中寻找。

	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}
		return false;
	}

2.2插入

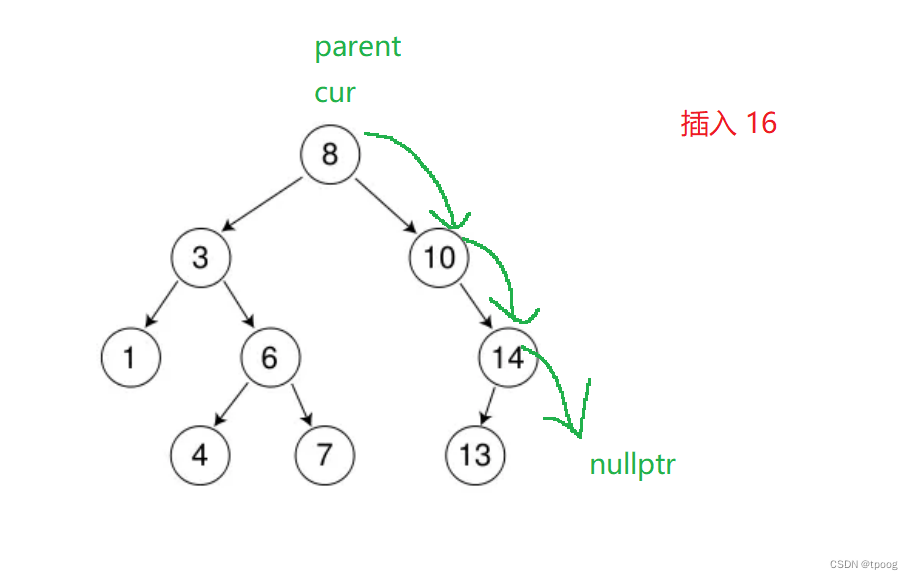
在这里插入图片描述
插入也很简单，例如上图我们要插入16，我们就先找到要插入的位置，然后为了方便我们记录整个过程我们需要一个父节点。

	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(key);
		if (parent->_key > key)
		{
			parent->_left=cur;
		}
		else
		{
			parent->_right=cur;
		}
		return true;
	}

现在可以进行测试代码的正确性。
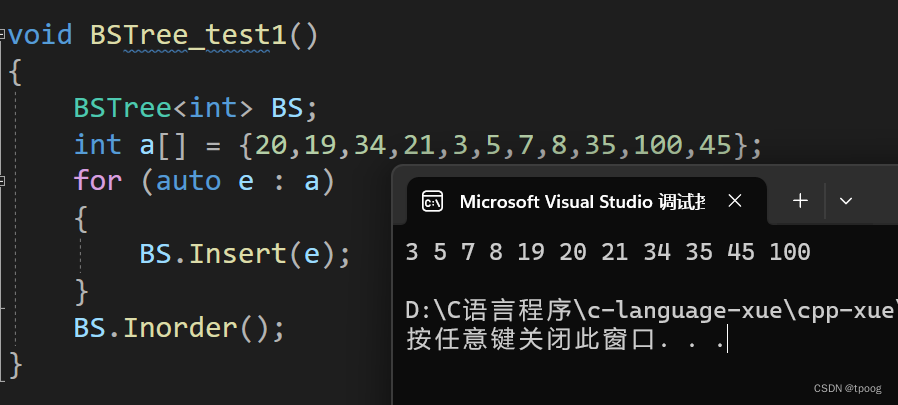
在这里插入图片描述
注意，搜索二插入要有序它走的是中序遍历。

2.3删除（重要）

删除比插入麻烦的多，我们删除值原则就是要保证它还是搜索二叉树，它的性质不可以改变。这就挺麻烦的，所以我们在删除这里用替换删除
替换删除：找到一个可以替换的节点，交换值，转换删除它。
可以替换的节点是：左子树的最大or右子树的最小。

下面我们来分析一下删除的各种情况

  1. 删除孩子节点
  2. 删除只有一个孩子的节点
  3. 删除两个孩子的节点
    这里总结下，情况1和2可以归为一类。情况3我们就要用到替换删除法

情况1(无孩子&&一个孩子）

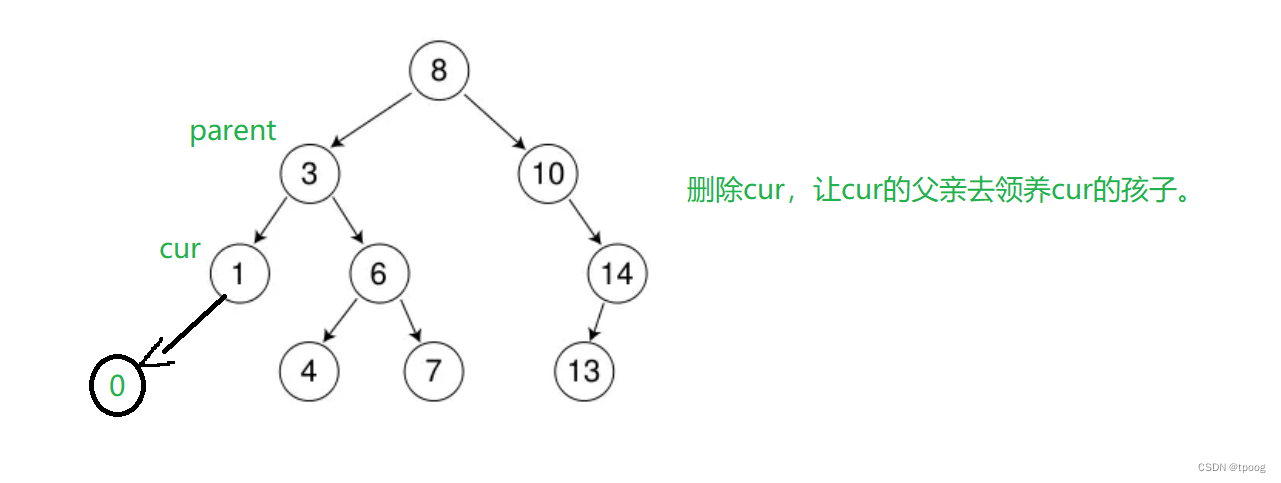
在这里插入图片描述

//找到了开始删除
				//第一种
				if (cur->_left == nullptr)//我的左为空
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_left)//我是父亲的左
						{
							parent->_left = cur->_right;
						}
						else//我是父亲的左
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
					return true;
				}
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}
					delete cur;
					return true;
				}

###情况二（两个孩子）
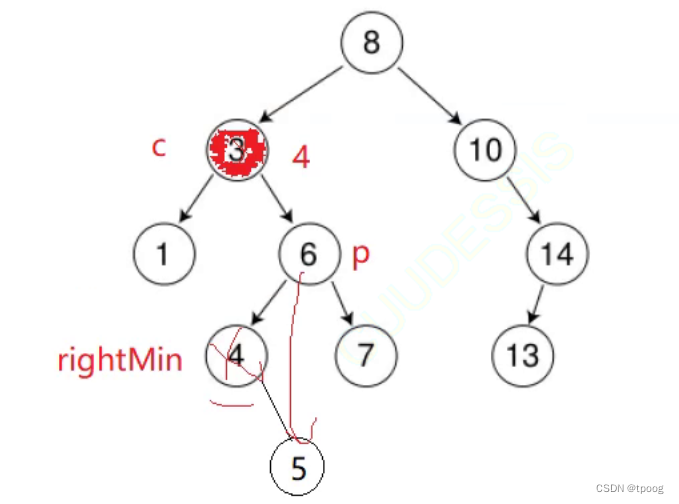
在这里插入图片描述
找到右子树的最小，把它的值复制给cur，就转换成了删除叶子节点

				else//第二种(俩孩子)替换删除法
				{
					Node* rightMinparent = cur;
					Node* rightMin = cur->_right;
					while (cur->_right)
					{
						rightMinparent = rightMin;
						rightMin = rightMin->_left;
					}
					cur->_key = rightMin->_key;
					if (rightMin == rightMinparent->_left)
					{
						rightMinparent->_left = rightMin->_right;
					}
					else
					{
						rightMinparent->_right = rightMin->_right;
					}
					delete rightMin;
					return true;
				}

3.二叉搜索树的应用

3.1K模型

K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到
的值。
比如：给一个单词word，判断该单词是否拼写正确。这个就是普通的二叉搜索树

3.2KV模型

KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。
通过key值快速查找另外一个值在不在。我们用二叉搜索树这个用的是比较多的
生活中的KV模型例如：商场车库，进去都可以进入（记录车牌（key）进入时间（value））
出：付费出（通过车牌（key），查询进入的时间（value））。
还有字典查询，高铁身份证进站等等。

3.2.1KV模型的实现

这个就是多加了一个对象，实现直接CV上面的代码

namespace key_value
{
	template<class K, class V>
	struct BSTreeNode
	{
		typedef BSTreeNode<K, V> Node;
		Node* _left;
		Node* _right;
		K _key;
		V _value;

		BSTreeNode(const K& key, const V& value)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
			, _value(value)
		{}
	};


	template<class K, class V>
	class BSTree
	{
		typedef BSTreeNode<K, V> Node;
	public:
		//插入
		bool Insert(const K& key, const V& value)
		{
			if (_root == nullptr)
			{
				_root = new Node(key, value);
				return true;
			}
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return true;
				}
			}

			cur = new Node(key, value);
			if (parent->_key < key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}
			return true;
		}
		//
		Node* Find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else
				{
					return cur;
				}
			}
			return nullptr;
		}
		//中序遍历
		void _InOrder(Node* root)
		{
			if (root == nullptr)
				return;
			_InOrder(root->_left);
			std::cout << root->_val << " ";
			_InOrder(root->_right);
		}

		void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}
		//3.删除
		bool Erase(const K& key)
		{
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_val < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_val > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					//找到了开始删除
					//第一种（无孩子&&一个孩子）
					if (cur->_left == nullptr)//我的左为空
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (parent->_left == cur)
							{
								parent->_left = cur->_right;
							}
							else//我是父亲的右节点
							{
								parent->_right = cur->_right;
							}
						}
						delete cur;
						return true;
					}
					else if (cur->_right == nullptr)//我的右为空
					{
						if (cur == _root)
						{
							_root = cur->_left;
						}
						else
						{
							if (parent->_left == cur)
							{
								parent->_left = cur->_left;
							}
							else//我是父亲的右节点
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
						return true;
					}

					else//第二种（有两个孩子）替换删除法
					{
						Node* rightMinparent = cur;
						Node* rightMin = cur->_right;
						while (rightMin->_left)
						{
							rightMinparent = rightMin;
							rightMin = rightMin->_left;
						}
						cur->_val = rightMin->_val;
						if (rightMin == rightMinparent->_left)
							rightMinparent->_left = rightMin->_right;
						else
							rightMinparent->_right = rightMin->_right;
						delete rightMin;
						return true;
					}
				}
			}
			return false;
		}
		//void InOrder()
		//{
		//	_InOrder(_root);
		//	cout << endl;
		//}
	//private:
	//	void _InOrder(Node* root)
	//	{
	//		if (root == nullptr)
	//			return;

	//		_InOrder(root->_left);
	//		cout << root->_key << " ";
	//		_InOrder(root->_right);
	//	}

	private:
		Node* _root = nullptr;
	};
}

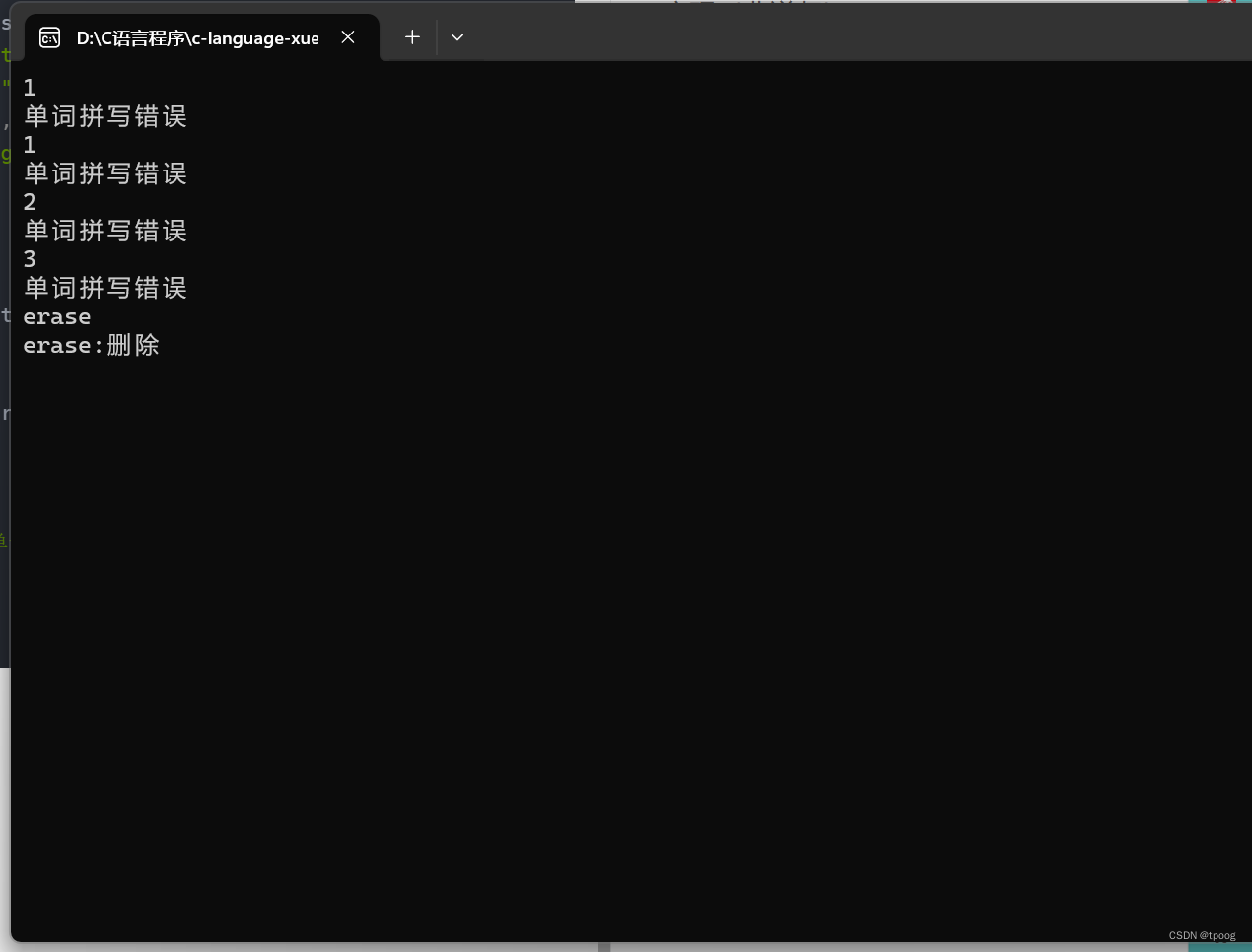
我们可以用哥=个例子来玩一玩这个KV模型

void TestBSTree()
{
	key_value::BSTree<string, string> dict;
	dict.Insert("insert", "插入");
	dict.Insert("erase", "删除");
	dict.Insert("left", "左边");
	dict.Insert("string", "字符串");

	string str;
	while (cin >> str)
	{
		auto ret = dict.Find(str);
		if (ret)
		{
			cout << str << ":" << ret->_value << endl;
		}
		else
		{
			cout << "单词拼写错误" << endl;
		}
	}
}

在这里插入图片描述

总结

总的来说二叉搜索树，比较难的地方就是删除部分，多画图多思考。
下篇我们就要深入二叉搜索树。

二叉搜索树源代码

#pragma once
#include<iostream>
using namespace std;
//struct BinarySearchTreeNode
template<class K>
struct BSTreeNode
{
	typedef BSTreeNode<K> Node;
	Node* _left;
	Node* _right;
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{}
};

//class BinarySearchTree
template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
	BSTree() = default;
	BSTree(const BSTree<K>& t)
	{
		_root = copy(t._root);
	}
	Node* copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;
		Node* newroot = new Node(root->_val);
		newroot->_left = copy(root->_left);
		newroot->_right = copy(root->_right);
		return newroot;
	}

	~BSTree()
	{
		Destroy();
	}
	void Destroy()
	{
		return _Destroy(_root);
	}
	void _Destroy(Node* root)
	{
		if (root == nullptr)
			return;
		_Destroy(root->_left);
		_Destroy(root->_right);
		delete root;
	}

	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}
		return false;
	}

	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(key);
		if (parent->_key > key)
		{
			parent->_left=cur;
		}
		else
		{
			parent->_right=cur;
		}
		return true;
	}
	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//找到了开始删除
				//第一种
				if (cur->_left == nullptr)//我的左为空
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_left)//我是父亲的左
						{
							parent->_left = cur->_right;
						}
						else//我是父亲的左
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
					return true;
				}
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}
					delete cur;
					return true;
				}
				else//第二种(俩孩子)替换删除法
				{
					Node* rightMinparent = cur;
					Node* rightMin = cur->_right;
					while (cur->_right)
					{
						rightMinparent = rightMin;
						rightMin = rightMin->_left;
					}
					if (rightMinparent->_left == rightMin)
					{
						rightMinparent->_left = rightMin->_right;
					}
					else
					{
						rightMinparent->_right = rightMin->_right;
					}
				}
			}
		}
		return false;
	}
	void Inorder()
	{
		_Inorder(_root);
		cout << endl;
	}
private:
	void _Inorder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_key << " ";
		_Inorder(root->_right);
	}
private:
	Node* _root=nullptr;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1572961.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

「每日跟读」英语常用句型公式 第4篇

「每日跟读」英语常用句型公式 第4篇

「每日跟读」英语常用句型公式 第4篇 1. I’ve decided to ____ 我决定要____了 I’ve decided to take a vacation (我决定要去度假) I’ve decided to change my lifestyle (我决定要改变我的生活方式) I’ve decided to adopt a dog (我决定要收养一条狗了) I’ve dec…
阅读更多...
【AOSP】手把手教你编译和调试AOSP源码

【AOSP】手把手教你编译和调试AOSP源码

一、下载AOSP源码 在开始之前&#xff0c;我们先安装编译AOSP需要的一些系统基本依赖&#xff0c;如下命令 sudo apt-get install git-core gnupg flex bison gperf build-essential zip curl zlib1g-dev gcc-multilib g-multilib libc6-dev-i386 lib32ncurses5-dev x11proto…
阅读更多...
三子棋游戏----C语言版【超级详细 + 视频演示 + 完整源码】

三子棋游戏----C语言版【超级详细 + 视频演示 + 完整源码】

㊙️小明博客主页&#xff1a;➡️ 敲键盘的小明 ㊙️ ✅关注小明了解更多知识☝️ 文章目录 前言一、三子棋的实现思路二、三子棋的实现步骤2.1 先显示游戏的菜单2.2 游戏的具体实现2.2.1 棋盘的初始化2.2.2 展示棋盘2.2.3 下棋&#x1f534;玩家下棋&#x1f534;电脑下棋2.2…
阅读更多...
OpenHarmony开发-系统烧录

OpenHarmony开发-系统烧录

本文详细介绍了烧录OpenHarmony系统到开发板的操作流程。从基础的硬件准备和软件环境设置入手&#xff0c;详细说明了如何配置开发环境、构建系统镜像等过程&#xff0c;详细描述了烧录过程中的关键步骤&#xff0c;以及如何使用专用工具将OpenHarmony系统镜像传输到开发板。同…
阅读更多...
【Rust】环境搭建

【Rust】环境搭建

Rust 支持很多的集成开发环境&#xff08;IDE&#xff09;或开发专用的文本编辑器。 官方网站公布支持的工具如下&#xff08;工具 - Rust 程序设计语言&#xff09; 本课程将使用 Visual Studio Code 作为我们的开发环境&#xff08;Eclipse 有专用于 Rust 开发的版本&#…
阅读更多...
vue使用iview导航栏Menu activeName不生效

vue使用iview导航栏Menu activeName不生效

activeName不生效 一、问题一、解决方案&#xff0c; 一、问题 根据ivew官网的提示&#xff0c;设置了active-name和open-names以后&#xff0c;发现不管是设置静态是数据还是设置动态的数据&#xff0c;都不生效 一、解决方案&#xff0c; 在设置动态名称的时候&#xff0c…
阅读更多...
docker笔记（一）：安装、常用命令

docker笔记（一）：安装、常用命令

一、docker概述 1.1docker为什么会出现 各种环境配置十分繁琐&#xff0c;每一个机器都需要配置环境&#xff0c;难免出现各种问题。 发布一个项目jar需要配置&#xff08;MySQL、redis、jdk、…&#xff09;&#xff0c;项目不能都带上环境安装打包&#xff1a; 传统&…
阅读更多...
Redis实战篇-集群环境下的并发问题

Redis实战篇-集群环境下的并发问题

实战篇Redis 3.7 集群环境下的并发问题 通过加锁可以解决在单机情况下的一人一单安全问题&#xff0c;但是在集群模式下就不行了。 1、我们将服务启动两份&#xff0c;端口分别为8081和8082&#xff1a; 2、然后修改nginx的conf目录下的nginx.conf文件&#xff0c;配置反向代…
阅读更多...
前端：注册页面（后端php实现）

前端：注册页面（后端php实现）

效果 代码 Regist.php <!-- 内部员工注册 --> <?php require_once get_db_conn.php; $conn db_connect();?> <?php //设置变量的默认值 if (!isset($_POST[UserID])) {$_POST[UserID] ; } if (!isset($_POST[Password])) {$_POST[Password] ; } if (!i…
阅读更多...
数据字典

数据字典

文章目录 一、需求分析二、表设计&#xff08;两张表&#xff09;三、功能实现3.1 数据字典功能3.1.1 列表功能3.1.2 新增数据字典3.1.3 编辑数据字典 3.2 数据字典明细3.2.1 列表功能3.2.2 新增字典明细3.2.3 编辑字典明细 3.3 客户管理功能3.3.1 列表功能3.3.2 新增用户3.3.3…
阅读更多...
【最新可用】Claude国内镜像,可上传图片,可用Claude3全系模型(包括Pro版本的Opus)!亲测比GPT好用!

【最新可用】Claude国内镜像,可上传图片,可用Claude3全系模型(包括Pro版本的Opus)!亲测比GPT好用!

亲测可用&#xff0c;镜像地址&#xff1a;Claude 3 镜像 使用方法 访问镜像&#xff1a;Claude 3 镜像 2. 点击设置&#xff0c;配置授权码&#xff0c;关闭设置。这里免费赠送一个体验版的授权码 sk-SZcJyvx3RXRID624E2D3795578Df44C7Af03F2909a8f5eA0 即可发起对话啦&…
阅读更多...
总包不足80w的高龄Android程序员，被面试官diss混得太差，网友狂吐槽……

总包不足80w的高龄Android程序员，被面试官diss混得太差，网友狂吐槽……

有网友直言&#xff1a;90%的人一辈子一年也拿不到80万 有网友分析到&#xff1a;看面试情况&#xff0c;没什么希望就直接其实我觉得30岁年薪低于1000万的都是loser&#xff0c;你我都是 有网友说&#xff1a;这几年互联网行业极大发展&#xff0c;让互联网行业成为了明星行…
阅读更多...
Python-VBA编程500例-033(入门级)

Python-VBA编程500例-033(入门级)

角色定位(Role Positioning)在编程中的实际应用场景主要体现在以下几个方面&#xff1a; 1、权限管理&#xff1a;在开发企业级应用或复杂的系统时&#xff0c;角色定位用于定义和管理用户的权限。例如&#xff0c;一个系统可能有管理员、普通用户、访客等不同角色&#xff0c…
阅读更多...
CSS设置字体样式

CSS设置字体样式

目录 前言&#xff1a; 1.font-family&#xff1a; 2.font-style&#xff1a; 3.font-weight&#xff1a; 4.font-size&#xff1a; 5.font-variant&#xff1a; 6.font&#xff1a; 前言&#xff1a; 在网页中字体是重要的组成部分&#xff0c;使用好字体可以让网页更…
阅读更多...
手动实现Tomcat底层机制+自己设计Servlet

手动实现Tomcat底层机制+自己设计Servlet

文章目录 1.Tomcat整体架构分析自己理解 2.第一阶段1.实现功能2.代码1.TomcatV1.java 3.调试阶段1.阻塞在readLine导致无法返回结果 4.结果演示 3.第二阶段1.实现功能2.代码1.RequestHander.java2.TomcatV2.java 3.调试阶段1.发现每次按回车会接受到两次请求 4.结果演示 4.第三…
阅读更多...
基于Spring Boot的简历系统设计与开发

基于Spring Boot的简历系统设计与开发

基于Spring Boot的简历系统设计与开发 开发语言&#xff1a;Java框架&#xff1a;springbootJDK版本&#xff1a;JDK1.8数据库工具&#xff1a;Navicat11开发软件&#xff1a;eclipse/myeclipse/idea 部分系统展示 前台首页界面 简历模板管理界面 用户管理界面 管理员登录界…
阅读更多...
C++设计模式：策略模式（二）

C++设计模式：策略模式（二）

1、定义与动机 定义一系列算法&#xff0c;把它们一个个封装起来&#xff0c;并且使它们可互相替换&#xff08;变化&#xff09;&#xff0c;该模式使得算法可独立于使用它的客户程序&#xff08;稳定&#xff09;而变化&#xff08;扩展&#xff0c;子类化&#xff09; 在软…
阅读更多...
pinia 的介绍和使用

pinia 的介绍和使用

pinia是vue2,vue2 尤其是vue3官方推荐的状态管理器&#xff0c;和vuex类似&#xff0c;但使用起来更为简单&#xff0c; 概念&#xff1a; state:定义响应式共享变量 getter&#xff1a;相当于计算属性 actions&#xff1a;相当于方法 npm安装 npm install pinia创建pinia ,注…
阅读更多...
【Python】常见容器

【Python】常见容器

Python容器 列表元组字符串集合字典 列表 定义方法&#xff1a;[元素1, 元素2, …] 列表一次可以存储多个不同数据类型的数据&#xff0c;支持嵌套。 例如&#xff1a; list1 ["张三", 33, True] print(list1) print(type(list1))list2 [list, "李四", …
阅读更多...
企业数据资产评估的财报显性化及数据资产入表的主要应用场景

企业数据资产评估的财报显性化及数据资产入表的主要应用场景

一、背景 近年来&#xff0c;企业“数据资产”的概念不断受政府/企业重视和建设.根据《数据资产评估指导意见》规定&#xff0c;数据资产评估是指资产评估机构及其资产评估专业人员遵守法律、行政法规和资产评估准则&#xff0c;根据委托对评估基准日特定目的下的数据资产价值…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023