(4条消息) 第五课、Trie树、并查集、堆和堆排序_yan__kai_的博客-CSDN博客
活动 - AcWing
并查集作用:一群元素将可以归类到一个代表元素上。可以维护元素到根节点的距离。可以维护每个并查集的大小。
基本操作回顾基础课,特别是“食物链”那道题
目录
例题
1.格子游戏
2.搭配购买(并查集+01背包)
3.程序自动分析(离散化)
4.银河英雄传说(维护距离)
编辑 编辑
5.奇偶分析
带边权的并查集
带扩展域的并查集
例题
1.格子游戏

画一条边可以将两个点连通,当出现封圈时,会将两个已经连通的点再连通。因此并查集处理连通块即可。
tips:把二维坐标压缩成一维坐标方便使用并查集。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=40010;
int n,m;
int p[N];
int get(int x,int y)
{
return x*n+y;
}
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
cin>>n>>m;
for(int i=0;i<=n*n;i++) p[i]=i;
int t=-1;
for(int i=1;i<=m;i++)
{
int a,b;
char d;
cin>>a>>b>>d;
a--,b--;
int x,y;
if(d=='D')
x=a+1,y=b;
else
x=a,y=b+1;
int p1=get(a,b),p2=get(x,y);
if(find(p1)==find(p2))
{
t=i;
break;
}
p[find(p1)]=p[find(p2)];
}
if(t==-1)
puts("draw");
else
cout<<t;
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/5133179/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。2.搭配购买(并查集+01背包)

将捆绑购买的云朵加入一个并查集,并查集需要维护云朵的价值和代价,与维护并查集的大小类似。注意不要加错了。
并查集处理完之后,做01背包即可。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N =10010;
int f[N];
int n,m,vol;
int p[N];
int v[N],w[N];
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
cin>>n>>m>>vol;
for(int i=1;i<=n;i++)
cin>>v[i]>>w[i];
for(int i=1;i<=n;i++) p[i]=i;
for(int i=0;i<m;i++)
{
int a,b;
cin>>a>>b;
int pa=find(a),pb=find(b);
if(pa!=pb)
{
v[pb]+=v[pa];
w[pb]+=w[pa];
p[pa]=pb;
}
}
for(int i=1;i<=n;i++)
{
if(p[i]==i)
for(int j=vol;j>=v[i];j--)
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
cout<<f[vol];
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/5133239/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。3.程序自动分析(离散化)

如果相等,就合并。如果不相等,发现我们并不能做出什么动作,只能说明这两个数不在一个集合,但是不好在之后的判断中限定。
因此先处理所有相等条件,再判断约束条件即可。
发现i,j范围1e9,直接开数组空间爆了,所以需要离散化。离散化不需要维持数字的顺序,所以不需要排序判重二分,直接开一个hash表即可。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_map>
using namespace std;
const int N =2e5+10;
int p[N];
int n,m;
unordered_map<int,int> S;
struct Query{
int x,y,e;
}query[N];
int get(int x)
{
if(S.count(x)==0) S[x]=++n;
return S[x];
}
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
int T;
cin>>T;
while(T--)
{
cin>>m;
S.clear();
n=0;
for(int i=0;i<m;i++)
{
int x,y,e;
scanf("%d%d%d",&x,&y,&e);
query[i]={get(x),get(y),e};
}
for(int i=1;i<=n;i++)
p[i]=i;
for(int i=0;i<m;i++)
{
if(query[i].e==1)
{
int pa=find(query[i].x),pb=find(query[i].y);
p[pa]=pb;
}
}
bool has_conflict=false;
for(int i=0;i<m;i++)
{
if(query[i].e==0)
{
int pa=find(query[i].x),pb=find(query[i].y);
if(pa==pb)
{
has_conflict=true;
break;
}
}
}
if(has_conflict) puts("NO");
else puts("YES");
}
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/5133509/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。4.银河英雄传说(维护距离)
看要求的两个操作:接在同一列,这个用并查集维护即可
判断间隔了多少艘战舰,那么我们需要维护节点到根节点的距离,把根节点作为排头即可。在合并过程中也需要思考怎么更新合并进来的结点的距离。
并查集路径压缩过程维护到根节点距离:路径压缩是让x一步指向根节点,则距离即x到原根节点的dist加上压缩之后,原根节点到新根节点的距离
int find(int x)
{
if(p[x]!=x)
{
int root=find(p[x]);
d[x]+=d[p[x]];
p[x]=root;
}
return p[x];
}
合并过程更新距离:把新一列接在队尾,等价于直接把新一列接到根节点,但是新一列的根节点要向接收列的根节点连一条size[接收列]长度的边即可。那么路径压缩之后,新一列的所有节点到根节点的长度都会加size,满足条件。
答案为。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N =30010;
int m;
int p[N],s[N],d[N];
int find(int x)
{
if(p[x]!=x)
{
int root=find(p[x]);
d[x]+=d[p[x]];
p[x]=root;
}
return p[x];
}
int main()
{
cin>>m;
for(int i=1;i<N;i++)
{
p[i]=i;
s[i]=1;
}
while(m--)
{
char op[2];
int a,b;
scanf("%s%d%d",op,&a,&b);
if(op[0]=='M')
{
int pa=find(a),pb=find(b);
if(pa!=pb)
{
d[pa]=s[pb];
s[pb]+=s[pa];
p[pa]=pb;
}
}
else
{
int pa=find(a),pb=find(b);
if(pa!=pb)
puts("-1");
else
{
cout<<max(abs(d[a]-d[b])-1,0)<<endl;
}
}
}
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/5133756/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。5.奇偶分析

求一段区间的数据,我们可以考虑用前缀和数组能否挖掘出某些性质。
AcWing 239. 奇偶游戏 - AcWing题解作者Bug-Free
发现与sum数组的奇偶性有关,并且是等价关系。


接着分析判断情况。
带边权的并查集
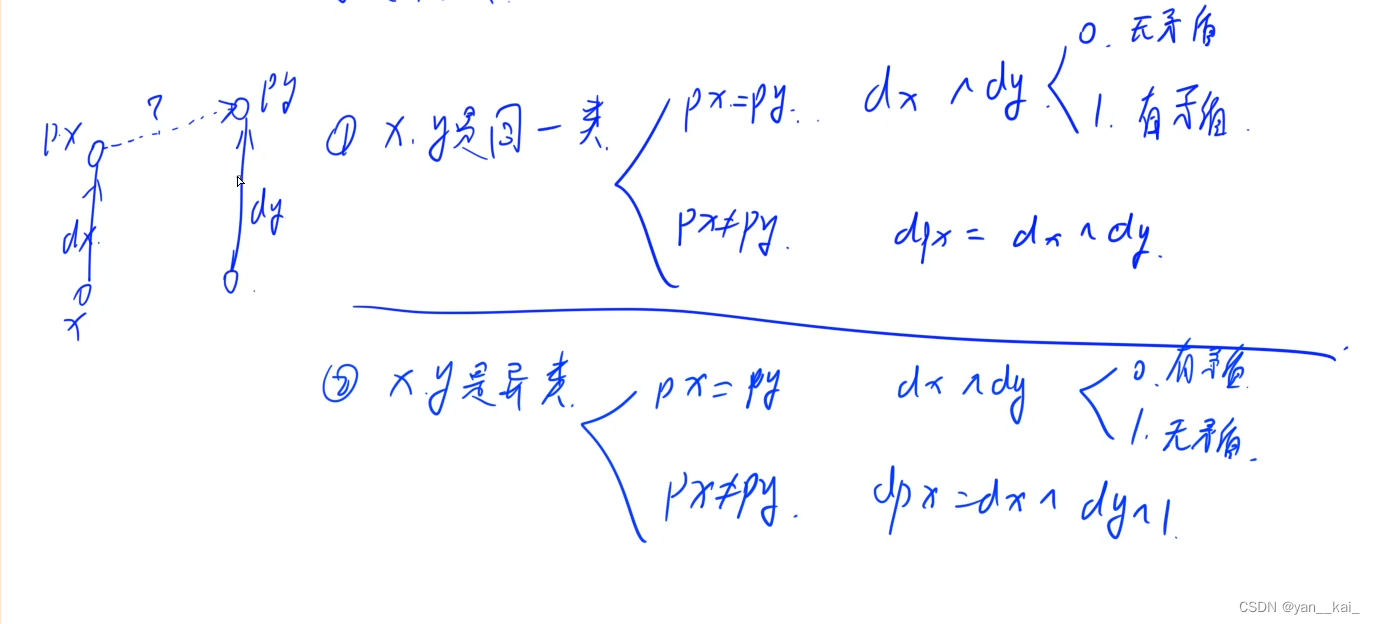
和食物链那道题相似。如果给出两点的相关关系,则并入一个并查集,维护到根节点的距离d,为偶数则同类,奇数则不同类,模2之后只有0和1。则可以由距离推出任意两点的关系。
在合并时,根据根节点同不同类判断。
分为两种情况:之前没提到过即px!=py,,和之前提到过px==py。
如果提到过,则判断是否符合要求,即x到根节点的距离或上y到根节点的距离求异或值,则或之后的值为t则不矛盾。
如果没提到过,则合并,px到py的距离d需要满足:
如果是x,y是奇偶性相同,则dx+d+dy==0 即d=-dx-dy,d=dx^dy
如果不同,d==-dx-dy-1 d=dx^dy^1
统一一下就是dx^dy^t
综上:
如果px不等于py,合并,更新d(px)=dx^dy^t
如果等于,判断dx^dy==t
由数据范围可知,同样需要离散化。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<unordered_map>
using namespace std;
const int N =20010;
int n,m;
int p[N],d[N];
unordered_map<int,int> S;
int get(int x)
{
if(S.count(x)==0) S[x]=++n;
return S[x];
}
int find(int x)
{
if(p[x]!=x)
{
int root=find(p[x]);
d[x]+=d[p[x]];
p[x]=root;
}
return p[x];
}
int main()
{
cin>>n>>m;
n=0;
for(int i=0;i<N;i++) p[i]=i;
int res=m;
for(int i=0;i<m;i++)
{
int a,b;
string type;
cin>>a>>b>>type;
a=get(a-1),b=get(b);
int t=0;
if (type == "odd") t = 1;
int pa=find(a),pb=find(b);
if(pa==pb)
{
if(((d[a] + d[b]) % 2 + 2) % 2 != t)
{
res=i;
break;
}
}
else
{
p[pa]=pb;
d[pa]=d[a]^d[b]^t;
}
}
cout<<res;
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/5134536/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。带扩展域的并查集
原数据有1~n,每个点有奇偶两种情况,我们用i+n表示这个点的另一种情况。
若没合并过:
如果给定x,y不同类,则说明x+n和y同类,x和y+n同类,x+n和y+n不同类。则合并同类情况。
如果给定x,y同类,则x+n和y+n同类,其他不同类。
如果合并了:
如果给定x y不同类,则判断x和y是否合并或者x+n和y+n是否合并,如果已合并,则矛盾。如果未合并,则合并x+n和y,y+n和x
如果给定同类,则判断x+n和y或者y+n和x是否合并。如果和并则矛盾。否则合并x和y ,x+n和y+n。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<unordered_map>
using namespace std;
const int N =20010,base = N / 2;
int n,m;
int p[N],d[N];
unordered_map<int,int> S;
int get(int x)
{
if(S.count(x)==0) S[x]=++n;
return S[x];
}
int find(int x)
{
if(p[x]!=x)
p[x]=find(p[x]);
return p[x];
}
int main()
{
cin>>n>>m;
n=0;
for(int i=0;i<N;i++) p[i]=i;
int res=m;
for(int i=0;i<m;i++)
{
int a,b;
string type;
cin>>a>>b>>type;
a=get(a-1),b=get(b);
if (type == "even")
{
if(find(a+base)==find(b))
{
res=i;
break;
}
p[find(a)]=find(b);
p[find(a+base)]=find(b+base);
}
else
{
if(find(a)==find(b))
{
res=i;
break;
}
p[find(a+base)]=find(b);
p[find(a)]=find(b+base);
}
}
cout<<res;
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/5134536/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。