本文用于个人算法竞赛学习,仅供参考
目录
一.质数的判定
二.分解质因数
三.质数筛
1.朴素筛法
2.埃氏筛法
3.线性筛法
四.约数
1.求一个数的所有约数
2.约数个数和约数之和
3.欧几里得算法(辗转相除法)-- 求最大公约数
一.质数的判定
质数:质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的数。常见的质数有2, 3, 5, 7, 11等。质数也被称为素数。
试除法:时间复杂度:O(n^ 1/2)

bool is_prime(int n)
{
if (n < 2)
return false;
for (int i = 2; i <= n / i; i++) //如果存在 a ÷ b = c , 那么就有 a ÷ c = b;
{
if (n % i == 0)
{
return false;
}
}
return true;
}二.分解质因数

试除法:时间复杂度:O(n^ 1/2)
//存放分解后质数的个数
unordered_map<int, int> primes;
void divide(int n)
{
//从2开始试除
for (int i = 2; i <= n / i; i++)// i^2 <= n
{
//合数进不来,因为被前面的质数约去了
if (n % i == 0)
{
while (n % i == 0)
{
primes[i]++;
n /= i;
}
}
}
if (n > 1)
primes[n]++;
}
int main()
{
divide(84);
for (auto prime: primes)
{
cout << prime.first << ':' << prime.second << endl;
}
return 0;
}三.质数筛
问题:给定一个n,筛出2~n的所有质数
1.朴素筛法
假设一个数n,它的因数有a, 那么n的因数a一定小于n,所以只需要通过a的倍数就能筛掉n,所以朴素筛法就是从2到n筛掉它们的倍数,最后剩下的就是质数。
时间复杂度:N(1 + 1/2 + 1/3 + ... + 1/n) = N*lnN, O(N*lnN);

可以发现同一个数可能会被筛掉多次,当样本个数非常多的时候是非常浪费时间的,要如何优化降低对一个数筛的次数呢?
2.埃氏筛法
埃氏筛法是对上面朴素筛法的优化,只筛掉质数的倍数,来减少筛掉同一个数的次数。
埃氏筛法(Sieve of Eratosthenes)是一种用来找出一定范围内所有素数的算法。其基本思想是从2开始,不断地将质数的倍数标记为非质数,最终剩下的即为质数。

筛掉4的倍数时,其实在筛掉2的倍数时就筛掉了,因为4是2的倍数,4的倍数也是2的倍数,所以4就没必要再去筛掉它的倍数了;对于一个合数,总会有它的质数代替它来筛掉它的倍数。
质数定理指出,小于给定数n的质数个数约为 n / ln(n)。
优化后时间O(N*loglogN)
const int N = 100;
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{
for (int i = 2; i <= n; i++)
{
if (st[i])
continue;
primes[cnt++] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
}

我们发现还是存在对同一个数多次筛掉的情况,如12被2和3筛掉两次,还能再优化吗?
3.线性筛法
线性筛法是一种在O(n)的复杂度情况下,筛选出2~n的所有质数。
它的原理是,从2开始,每次找到一个最小的质数,然后把它的倍数都标记为非质数,即每个数合数只会被它的最小质因数筛掉。
比如上面的埃氏筛法,12会被2和3筛两次,线性筛法只会通过12的最小的质数2来筛掉。
最外层for循环遍历2~n,primes保存2~i的质数,内层for循环从小枚举质数
1.对于 primes[j] <= n / i;
如果i是合数,会走到 if (i % primes[j] == 0) break 结束掉
如果i是质数,会走到 primes[j] == i 后结束掉
所以不用担心存在越界问题
2.对于 if (i % primes[j] == 0) break;
若 i % primes[j] != 0, primes[j]一定小于i的最小质因子,primes[j] 一定是primes[j] * i 的最小质因子,因为primes从小到大枚举,且primes[j] 小于i
若i % primes[j] == 0,primes[j] 一定是i的最小质因子,primes[j] 一定是primes[j] * i 的最小质因子,因为primes从小到大枚举,且primes[j] 小于i
如果i % primes[j] == 0,就应该break了,为什么?
已知i % primes[j] == 0,就说明i是合数,i已经再前面通过k * primes[j] 筛掉了;
假设我们没有break,走到primes[j + 1], 会有 i * primes[j + 1], 代入得 k * primes[j] * primes[j + 1],很明显primes[j] < primes[j + 1], 说明一个数已经被primes[j] 筛掉过了,再通过primes[j]筛就重复了。
3.对于每一个合数x,一定会被筛掉,假设x的最小质因子为p,当i 遍历到x / p时,x一定会被筛掉。
4.每一个合数都会被它的最小质数筛掉,说明每个数只会被筛一次,所以是线性的,时间复杂度是O(n)。
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}四.约数
1.求一个数的所有约数
试除法:枚举 i <= n / i, 看i 是否是约数
vector<int> get_divisors(int n)
{
vector<int> result;
for (int i = 2; i <= n / i; i++)
{
if (n % i == 0)
{
result.push_back(i);
//避免加入同一个数
if (n / i != i)
result.push_back(n / i);
}
}
sort(result.begin(), result.end());
return result;
}2.约数个数和约数之和
给定一个数N,求N的约数个数
将N进行质因数分解p,有N = p1^c1 * p2^c2 * ... *pk^ck
对于每个质数p,c可以取0~c,则约数个数: (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和: (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)
思路:
由N = p1^c1 * p2^c2 * ... *pk^ck,约数和为(p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)
p比较好求,直接分解质因数就行,问题是(pk^0 + pk^1 + ... + pk^ck)要怎么求?
假设 t = 1,存在操作 t = p * t + 1;
则有t = p * 1 + 1 = p + 1
t = p * (p + 1) + 1 = p^2 + p + 1
t = p * (p^2 + p + 1) + 1 = p^3 + p^2 + p^1 + 1
……
typedef long long LL;
int mod = 1e9 + 7;
int main()
{
unordered_map<int, int> primes;
int n;
cin >> n;
while (n--)
{
int a;
cin >> a;
//对每个数进行质因数分解
for (int i = 2; i <= a / i; i++)
{
if (a % i == 0)
{
primes[i]++;
a /= i;
}
}
if (a > 1)
primes[a]++;
}
LL result = 1;
for (auto prime : primes)
{
LL t = 1;
int a = prime.first, b = prime.second;
while (b--)
{
t = (t * a + 1) % mod;
}
result = result * t % mod;
}
cout << result << endl;
return 0;
}常见模运算
(a * b) mod c = ((a mod c) * (b mod c)) mod c
(a + b) mod c = ((a mod c) + (b mod c)) mod c
(a - b) mod c = ((a mod c) - (b mod c)) mod c
(a ^ b) mod c = ((a mod c) ^ b) mod c
(a / b) mod c != ((a mod c) / (b mod c)) mod c除法的模运算不满足这样的等式
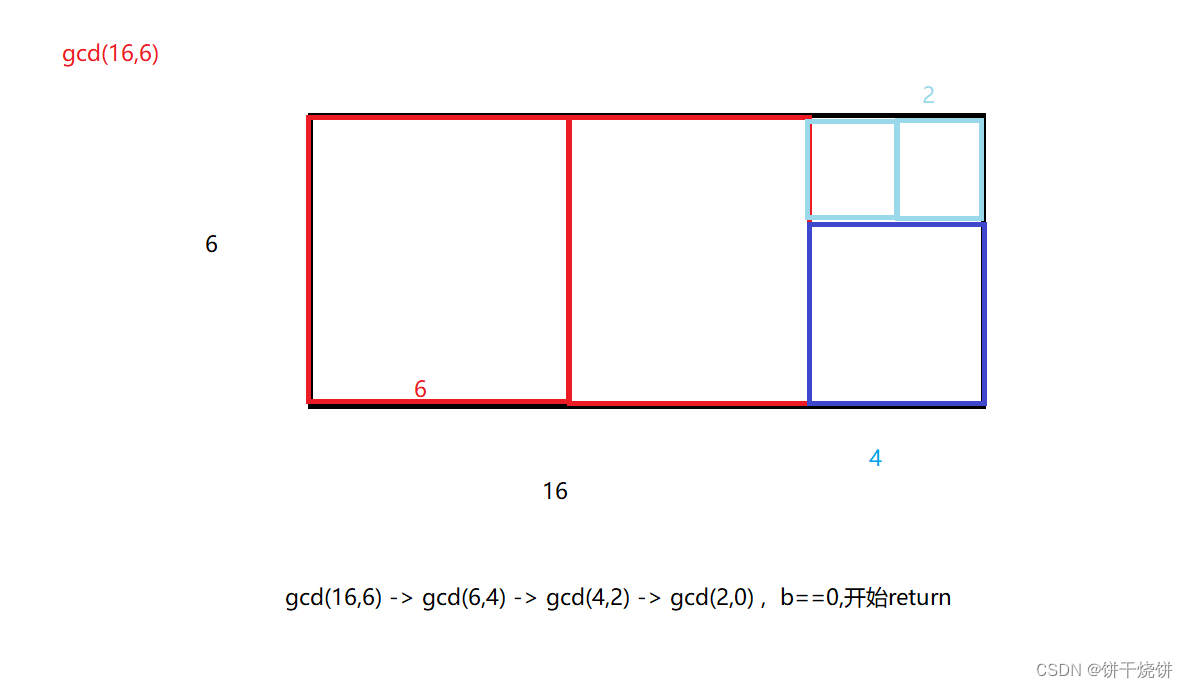
3.欧几里得算法(辗转相除法)-- 求最大公约数
gcd(a, b) = gcd(b, a mod b);
gcd代表最大公约数
int gcd(int a, int b)
{
//if (a < b) swap(a, b);//这一步不需要,因为会自己调整,比如gcd(6,16),下一次递归就变成了gcd(16,6)
return b ? gcd(b, a % b) : a;
}