目录
有向无环图DP
力扣 329. 矩阵中的最长递增路径
力扣 2192. 有向无环图中一个节点的所有祖先
有向有环图DP
力扣 1306. 跳跃游戏 III
有向无环图DP
力扣 329. 矩阵中的最长递增路径
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例 1:
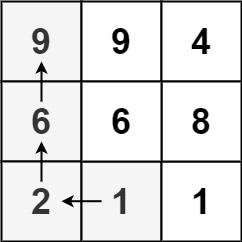
输入:matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
示例 2:
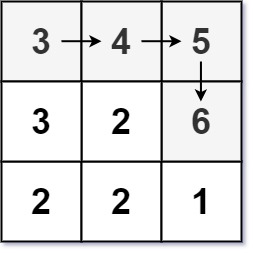
输入:matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3:
输入:matrix = [[1]]
输出:1
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
0 <= matrix[i][j] <= 231 - 1
class Solution {
public:
int id(int x, int y)
{
return x * col + y;
}
int longestIncreasingPath(vector<vector<int>>& matrix) {
col = matrix[0].size();
if (col == 1 && matrix.size() == 1)return 1;
map<int, vector<int>>m;
for (int i = 1; i < matrix.size(); i++)for (int j = 0; j < matrix[0].size(); j++)
if (matrix[i][j] < matrix[i - 1][j])m[id(i, j)].push_back(id(i - 1, j));
else if (matrix[i][j] > matrix[i - 1][j])m[id(i - 1, j)].push_back(id(i, j));
for (int i = 0; i < matrix.size(); i++)for (int j = 1; j < matrix[0].size(); j++)
if (matrix[i][j] < matrix[i][j - 1])m[id(i, j)].push_back(id(i, j - 1));
else if (matrix[i][j] > matrix[i][j - 1])m[id(i, j - 1)].push_back(id(i, j));
theans = 0;
next_.clear();
len.clear();
GetLongestPath(m);
return theans;
}
int col;
map<int, int>next_;//后继
map<int, int>len;//长度
int theans = 0;
int dp(map<int, vector<int>>& m, map<int, int>& ans, int id)
{
if (ans[id])return ans[id];
ans[id] = 1;
for (auto k : m[id]) {
if (ans[id] < dp(m, ans, k) + 1) {
ans[id] = dp(m, ans, k) + 1;
next_[id] = k;
}
}
theans = max(theans, ans[id]);
return ans[id];
}
//求有向无环图中每个点出发的最长路径
void GetLongestPath(map<int, vector<int>>& m)
{
for (auto& ai : m)
{
dp(m, len, ai.first);
}
}
};
力扣 2192. 有向无环图中一个节点的所有祖先
给你一个正整数 n ,它表示一个 有向无环图 中节点的数目,节点编号为 0 到 n - 1 (包括两者)。
给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。
请你返回一个数组 answer,其中 answer[i]是第 i 个节点的所有 祖先 ,这些祖先节点 升序 排序。
如果 u 通过一系列边,能够到达 v ,那么我们称节点 u 是节点 v 的 祖先 节点。
示例 1:

输入:n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]] 输出:[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]] 解释: 上图为输入所对应的图。 - 节点 0 ,1 和 2 没有任何祖先。 - 节点 3 有 2 个祖先 0 和 1 。 - 节点 4 有 2 个祖先 0 和 2 。 - 节点 5 有 3 个祖先 0 ,1 和 3 。 - 节点 6 有 5 个祖先 0 ,1 ,2 ,3 和 4 。 - 节点 7 有 4 个祖先 0 ,1 ,2 和 3 。
示例 2:
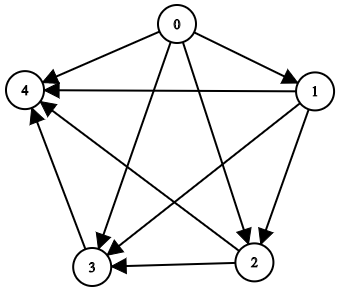
输入:n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]] 输出:[[],[0],[0,1],[0,1,2],[0,1,2,3]] 解释: 上图为输入所对应的图。 - 节点 0 没有任何祖先。 - 节点 1 有 1 个祖先 0 。 - 节点 2 有 2 个祖先 0 和 1 。 - 节点 3 有 3 个祖先 0 ,1 和 2 。 - 节点 4 有 4 个祖先 0 ,1 ,2 和 3 。
提示:
1 <= n <= 10000 <= edges.length <= min(2000, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi <= n - 1fromi != toi- 图中不会有重边。
- 图是 有向 且 无环 的。
class Solution {
public:
vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
m.clear();
g = DirectedGraphData<>(edges);
for (int i = 0; i < n; i++)dp(i);
vector<vector<int>>ans(n);
for (auto& mi : m) {
for (auto id : mi.second)ans[id.first].push_back(mi.first);
}
return ans;
}
void dp(int id)
{
if (m.find(id)!=m.end())return;
for (auto i : g.adjaList[id]) {
dp(i);
m[id][i] = 1;
for (auto mi : m[i])m[id][mi.first] = 1;
}
}
map<int, map<int, int>>m;
DirectedGraphData<>g;
};
有向有环图DP
力扣 1306. 跳跃游戏 III
这里有一个非负整数数组 arr,你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时,你可以跳到 i + arr[i] 或者 i - arr[i]。
请你判断自己是否能够跳到对应元素值为 0 的 任一 下标处。
注意,不管是什么情况下,你都无法跳到数组之外。
示例 1:
输入:arr = [4,2,3,0,3,1,2], start = 5 输出:true 解释: 到达值为 0 的下标 3 有以下可能方案: 下标 5 -> 下标 4 -> 下标 1 -> 下标 3 下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3
示例 2:
输入:arr = [4,2,3,0,3,1,2], start = 0 输出:true 解释: 到达值为 0 的下标 3 有以下可能方案: 下标 0 -> 下标 4 -> 下标 1 -> 下标 3
示例 3:
输入:arr = [3,0,2,1,2], start = 2 输出:false 解释:无法到达值为 0 的下标 1 处。
提示:
1 <= arr.length <= 5 * 10^40 <= arr[i] < arr.length0 <= start < arr.length
class Solution {
public:
bool canReach(vector<int>& arr, int start) {
if (start < 0 || start >= arr.size())return false;
if (m[start])return m[start] == 1;
if (arr[start] == 0)return true;
m[start] = 2;
if (canReach(arr, start - arr[start]) || canReach(arr, start + arr[start]))return m[start] = 1;
return !(m[start] = 2);
}
map<int, int>m;
};