文章目录
- 问题描述
- 问题建模
- 决策变量
- 数学建模
- 基于容量的消除子环的约束 (load-based SECs)
- CVRP完整的数学模型
- 加上时间窗限制的CVRP
问题描述
给定一个图,图上的点代表客户,边代表客户之间的路线,边的权重代表客户之间的距离,点上的数字代表每个用户的需求量。
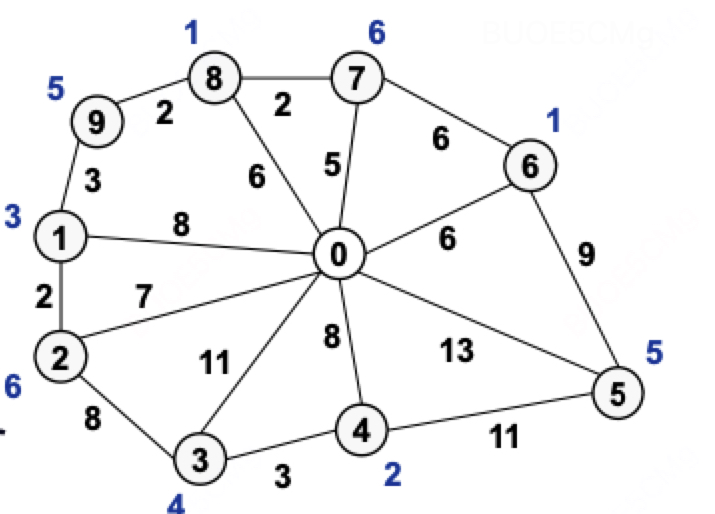
数学符号表示如下:

本文讨论的问题背景:
- 用户需求已知,且被一辆车满足(不要拆开);
- 有 m m m辆车,且有相同的最大载量 L L L;
- 路网络是对称的(往返距离一样,不考虑上下坡之类的问题);
- 要么取货要么送货;
- 1个仓库,而且车的路线 T T T要是闭环的(最后要回到仓库);
- 只考虑1个规划周期;
- 目标是最小化车辆的行驶距离;
- 点0代表仓库。
问题建模
决策变量

数学建模
疑问:这种建模方式怎么知道每辆车的路线?
会有图上的哪些边被选中,形成 m m m个环,就知道啦!
目标函数:最小化行驶距离
m a x ∑ i , j ∈ V , i ≠ j x i j ∗ c i j max \sum_{i,j \in V, i \neq j}x_{ij}*c_{ij} max∑i,j∈V,i=jxij∗cij
约束1:车辆从每个客户出发一次
∑ j ∈ V , i ≠ j x i j = 1 , ∀ i ∈ V − { 0 } \sum_{j \in V, i \neq j}x_{ij} = 1, \forall i \in V-\{0\} ∑j∈V,i=jxij=1,∀i∈V−{0}
约束2:车辆进入每个客户一次
∑ j ∈ V , i ≠ j x j i = 1 , ∀ i ∈ V − { 0 } \sum_{j \in V, i \neq j}x_{ji} = 1, \forall i \in V-\{0\} ∑j∈V,i=jxji=1,∀i∈V−{0}
约束3:最多用 m m m辆车
∑ j ∈ V − { 0 } x 0 j ≤ m \sum_{j \in V-\{0\}}x_{0j} \leq m ∑j∈V−{0}x0j≤m
如果只是上面的模型,可能会出现下图这种解,右下角这个环没有包含仓库!因此,我们需要一个约束去消除这种不包含仓库的子环。此外,上面的约束也没有约束车辆的容量限制!这也是VRP建模的一个略难的约束。
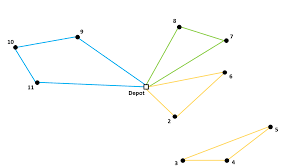
基于容量的消除子环的约束 (load-based SECs)
学术上称为Sub-tour-elimination constraints (SECs),该约束需要保证:
1. 每个环路不超过车辆最大容量;
2. 每个环路都包含仓库。
新引入一个变量:
u
i
u_i
ui: 假设我们的问题是车辆去客户那里取货,
u
i
u_i
ui表示车辆到达客户点
i
i
i时的载量,
∀
i
∈
V
\forall i \in V
∀i∈V;
因此有如下约束:
如果我们选择了 ( i , j ) (i, j) (i,j)这条连边,那么车辆到达客户 i i i时的容量,加上用户 i i i寄货的重量,要为车辆到达客户 j j j时的容量。逻辑上是相等的,但是我理解是为了刻画这个等式的成立是基于 ( i , j ) (i, j) (i,j)这条连边被选择,所以描述成了下面的 ≤ \leq ≤的形式。
u i + b i ≤ u j + ( 1 − x i j ) L , ∀ i , j ∈ V − 0 , i ≠ j u_i + b_i \leq u_j + (1-x_{ij})L, \forall i,j \in V -{0},i \neq j ui+bi≤uj+(1−xij)L,∀i,j∈V−0,i=j
但是这个约束并没有刻画车辆的容量限制?
应该还要加一个:
u
i
≤
L
,
∀
i
∈
V
u_i \leq L, \forall i \in V
ui≤L,∀i∈V
CVRP完整的数学模型

加上时间窗限制的CVRP
假设某些客户只想在特定时间段被服务,那么在上述问题的基础上,我们需要引入如下新的常量定义:

同时,我们需要引入一个新的决策变量:
a
i
a_i
ai:到达客户
i
i
i时的时间,
∀
i
∈
V
\forall i \in V
∀i∈V
新增的约束包括:
1. 定义到达第一个客户的时间:
t 0 j x i j ≤ a j , ∀ j ∈ V t_{0j}x_{ij} \leq a_j, \forall j \in V t0jxij≤aj,∀j∈V
2. 约束两个连续访问的用户的时间:访问用户 i i i的时间+用户 i i i被服务的时间+从 i i i到 j j j的形式时间 = 访问用户 j j j的时间
a i + s i + t i j ≤ a j + ( 1 − x i j ) T , ∀ i , j ∈ V − 0 , i ≠ j a_i + s_i + t_{ij} \leq a_j + (1-x_{ij})T, \forall i,j \in V-0, i \neq j ai+si+tij≤aj+(1−xij)T,∀i,j∈V−0,i=j
3. 约束每个用户被访问的时间在指定时间窗内:
w
i
s
≤
a
i
,
∀
i
∈
V
−
0
w_i^s \leq a_i, \forall i \in V-0
wis≤ai,∀i∈V−0
a
i
+
s
i
≤
w
i
e
,
∀
j
∈
V
−
0
a_i + s_i \leq w_i^e, \forall j \in V-0
ai+si≤wie,∀j∈V−0