目录
1.堆是什么?
2.问题引入:当我们插入一个新的元素时,那么他还是堆吗。
3.堆的元素插入
4.问题引入:当我们删除一个堆顶元素时,我们又该如何调整呢?
5.堆顶元素删除
6.如何建堆?
6.1向上调整建堆:
6.2向下调整建堆:
6.3 两者区别:
7.堆排序的实现:
1.堆是什么?
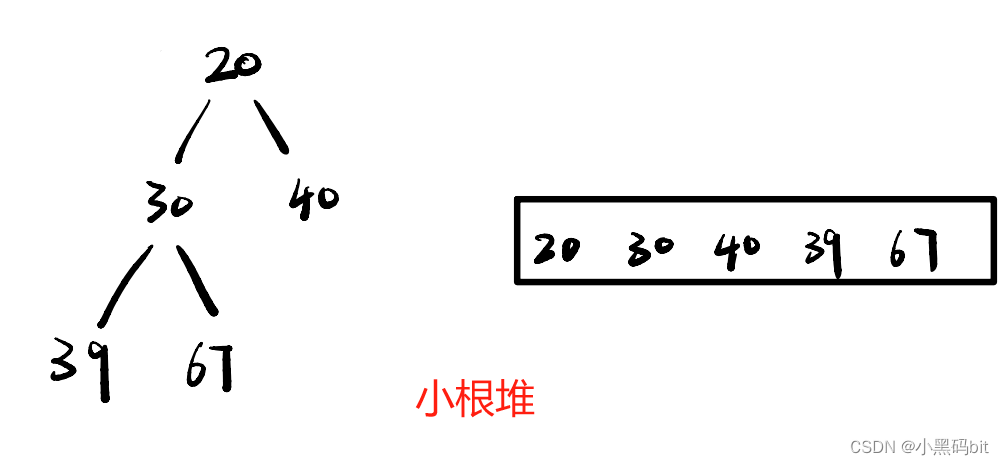
堆其实从逻辑上看是一棵完全二叉树,物理结构上来看就是一个顺序的数组。满足:任何一个非叶节点的值都不大于(或不小于)其左右孩子结点的值。若父亲大,孩子小叫做大根堆,若父亲小,孩子大叫做小根堆。
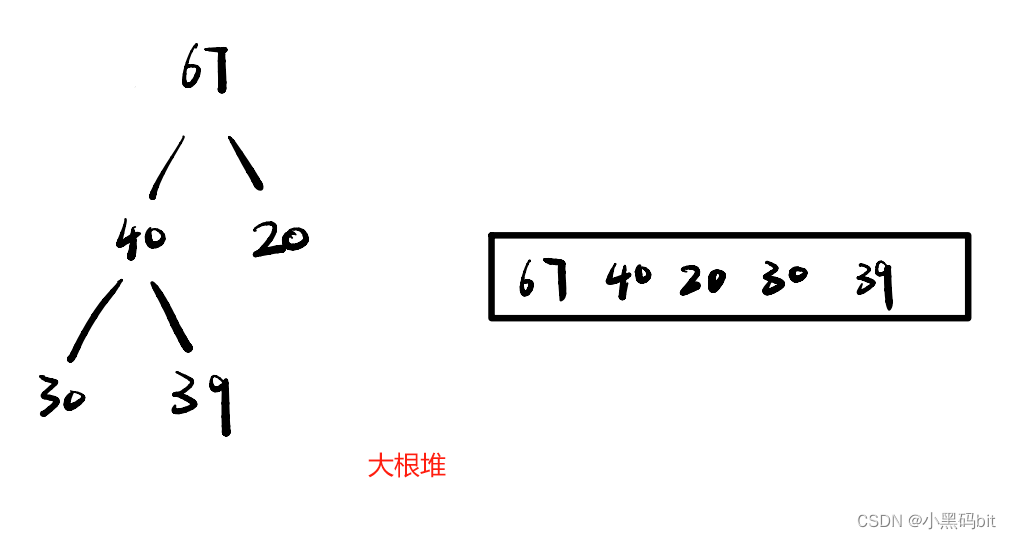
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
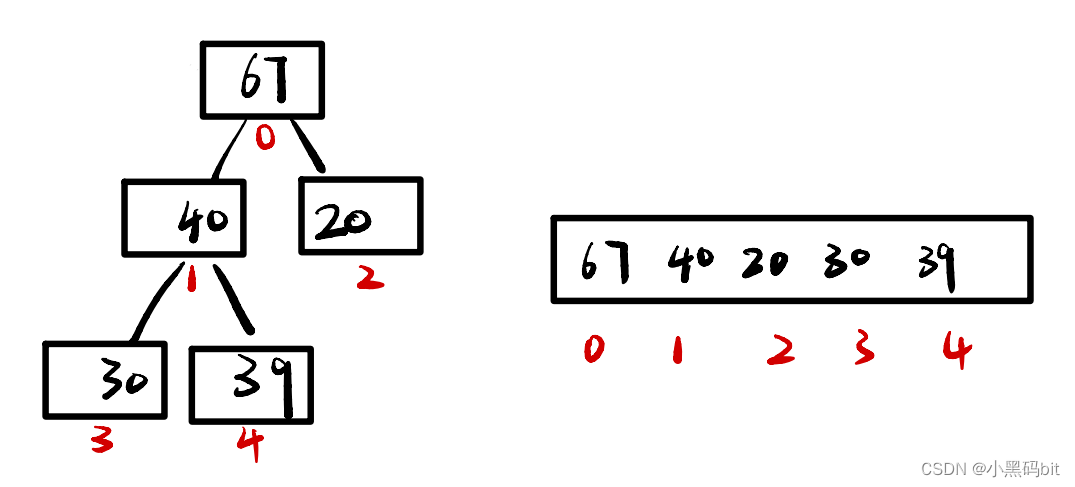
从这个树中我们可以看到,下标为奇数刚好为左孩子,下标为偶数刚好为右孩子。
由此我们可以得到孩子与父亲的关系
leftchild=parent*2+1;
rightchild=parent*2+2;
parent=(child-1)/2;
2.问题引入:当我们插入一个新的元素时,那么他还是堆吗。
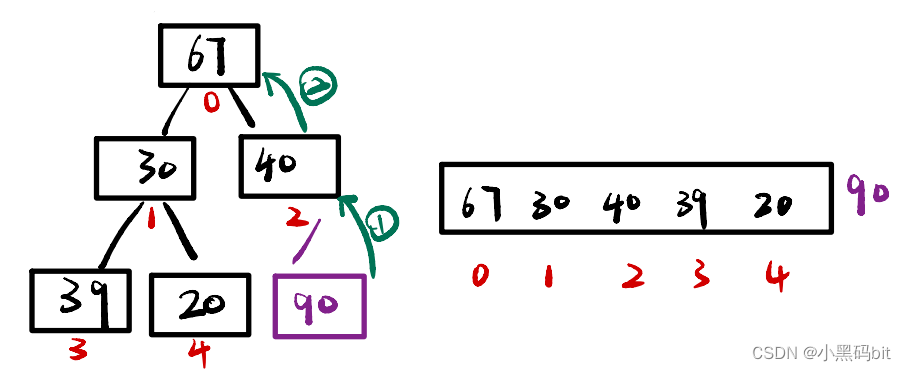
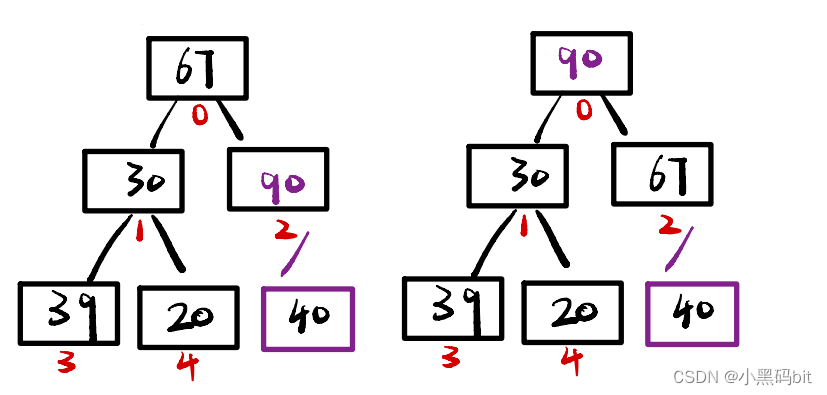
如果我们原来有一个堆,但我们又插入了新的数据,那么此时我们就需要进行向上调整,他是个大根堆,按照我们的顺序可以将他重新调整为大根堆。那么我们最容易误解的就是如果原本是个小根堆的话是不是就要向下调整呢?实际情况小根堆的新元素插入也是向上调整的,只不过就是元素的对比条件与大根堆不同,但代码逻辑都是向上比较的,都是一个爬升的过程。
代码展示
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child>0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}我们知道了堆增加元素后如何使他变成新的堆,那么我们就可以进行堆的插入操作了。
3.堆的元素插入
代码展示
void HeapPush(HP* hp, HPDataType x)
{
assert(hp);
if (hp->size == hp->capacity)
{
int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;//申请扩容
HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);//千万别忘了怎么扩容的
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
hp->capacity = newcapacity;
hp->a = tmp;
}
hp->a[hp->size] = x;
hp->size++;
AdjustUp(hp->a , hp->size - 1);
}考虑到我们的堆存储结构实际上是顺序结构,所以当我们插入元素可能会用到异地扩容。
4.问题引入:当我们删除一个堆顶元素时,我们又该如何调整呢?
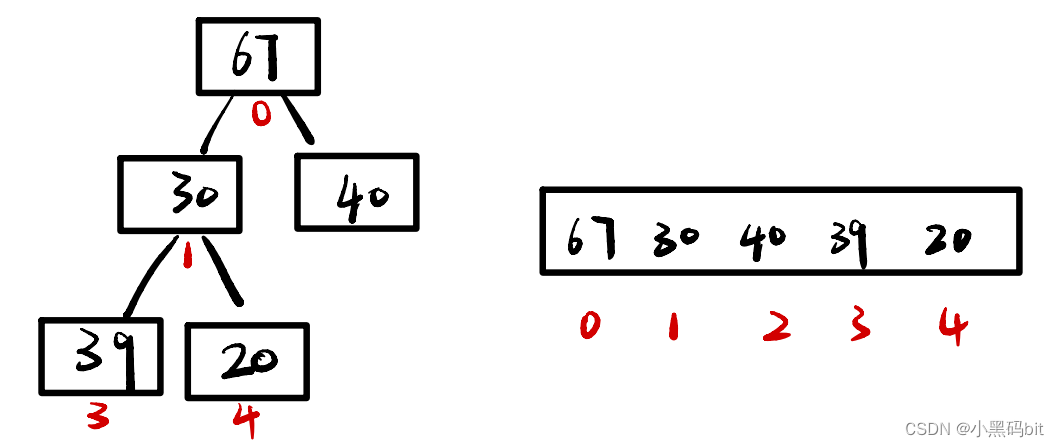
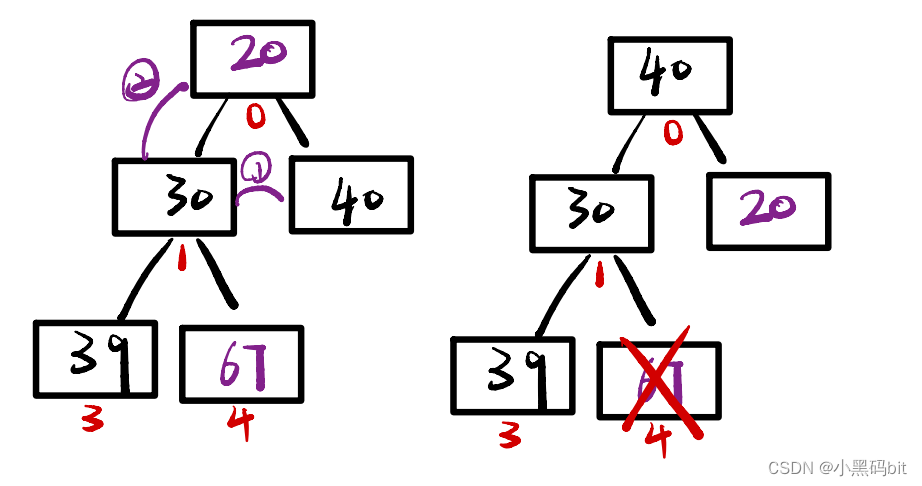
如图,为了方便操作,我们把堆底的元素和堆顶的元素进行了调换,这样我们可以保证他的逻辑结构还是一颗完全二叉树,方便我们进行调整操作。
此时,我们进行的是向下调整算法,我们可以观察出我们向下调整算法的前提:左右子树必须是一个堆,才能调整。
代码展示:
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child<n)//要分两个独立的判断 1.先判断孩子的大小,拿出一个最大的。2.然后拿出的最大的与根比较,最终决定是否交换位置
{
if (child+1 < n && a[child+1]> a[child])
{
child++;//指向大的孩子
}
if (a[child] > a[parent])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}我们知道了堆删除元素后如何使他变成新的堆,那么我们就可以进行堆的删除操作了。
5.堆顶元素删除
代码展示:
void HeapPop(HP* hp)
{
assert(hp);
assert(hp->size>0);
Swap(&hp->a[0] ,&hp->a[hp->size-1]);//这里忘记减一了
hp->size--;
AdjustDown(hp->a, hp->size, 0);
}6.如何建堆?
第一种方法就是,我们可以不断地插入新元素,然后再进行向上调整操作。实质上就是第二种方法中的向上调整建堆。
图解:
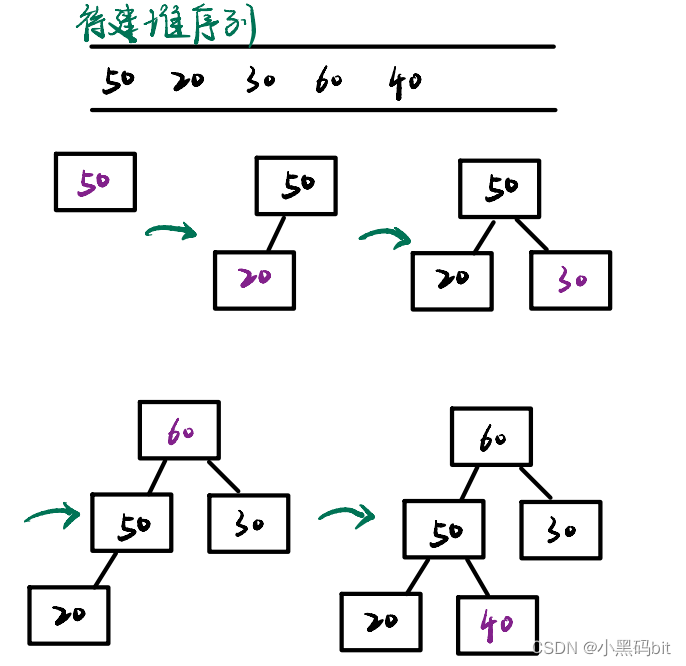
代码展示:
void HeapCreate(HP* hp, HPDataType* a, int n)
{
assert(hp);
HeapInit(hp);
for (int i = 0; i < n; ++i)
{
HeapPush(hp, a[i]);
}
}第二种方法是我们先开辟出一个新的数组,就是堆已有的数组进行调整,但是到底是向上调整还是向下调整我们又分为了两种情况:
6.1向上调整建堆:
图解建堆
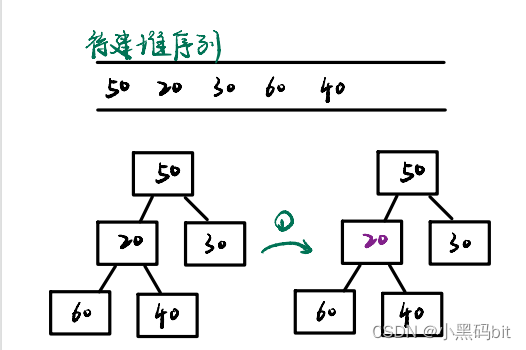
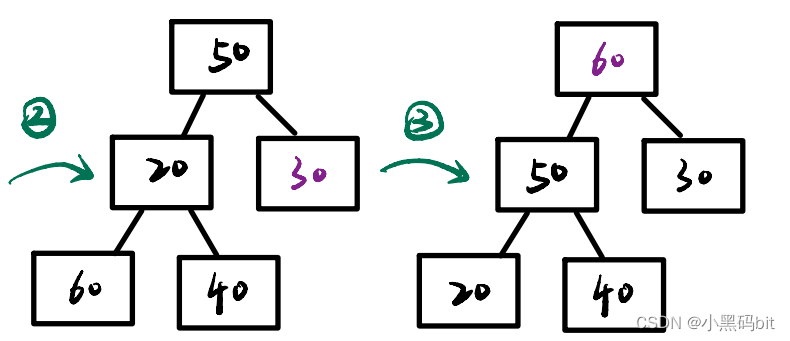
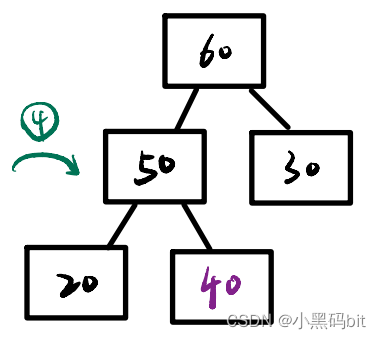
代码展示:
void HeapCreate(HP* hp, HPDataType* a, int n)
{
assert(hp);
hp->a = (HPDataType*)malloc(sizeof(HPDataType) * n);//千万别忘了怎么扩容的
if (hp->a == NULL)
{
perror("malloc fail");
exit(-1);
}
memcpy(hp->a, a, sizeof(HPDataType) * n);
hp->capacity = hp->size = n;
for (int i = 1; i<n ; ++i)
{
AdjustUp(hp->a, i);
}
}6.2向下调整建堆:
图解建堆:


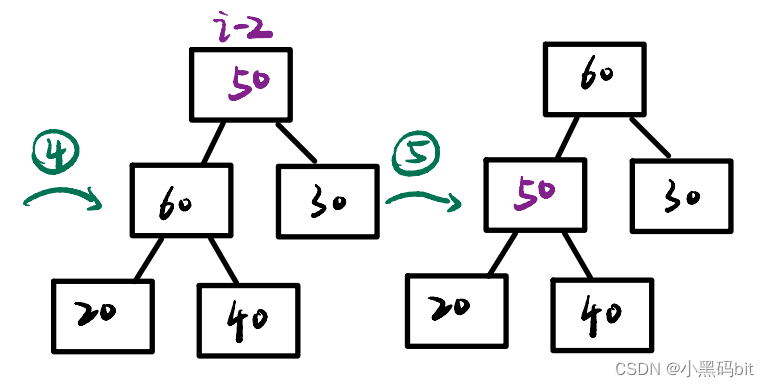
代码展示:
void HeapCreate(HP* hp, HPDataType* a, int n)
{
assert(hp);
hp->a = (HPDataType*)malloc(sizeof(HPDataType) * n);//千万别忘了怎么扩容的
if (hp->a == NULL)
{
perror("malloc fail");
exit(-1);
}
memcpy(hp->a, a, sizeof(HPDataType) * n);
hp->capacity = hp->size = n;
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(hp->a, n, i);
}
}6.3 两者区别:
向下调整时:
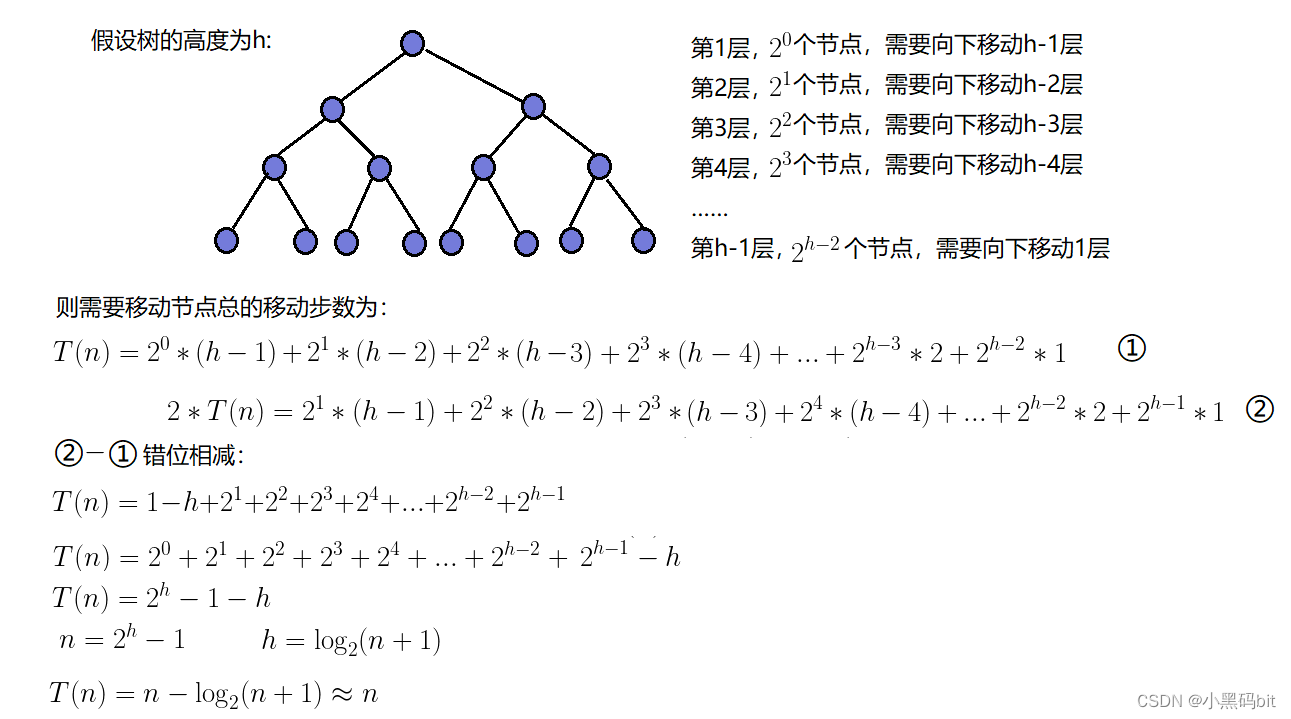
向上调整时:
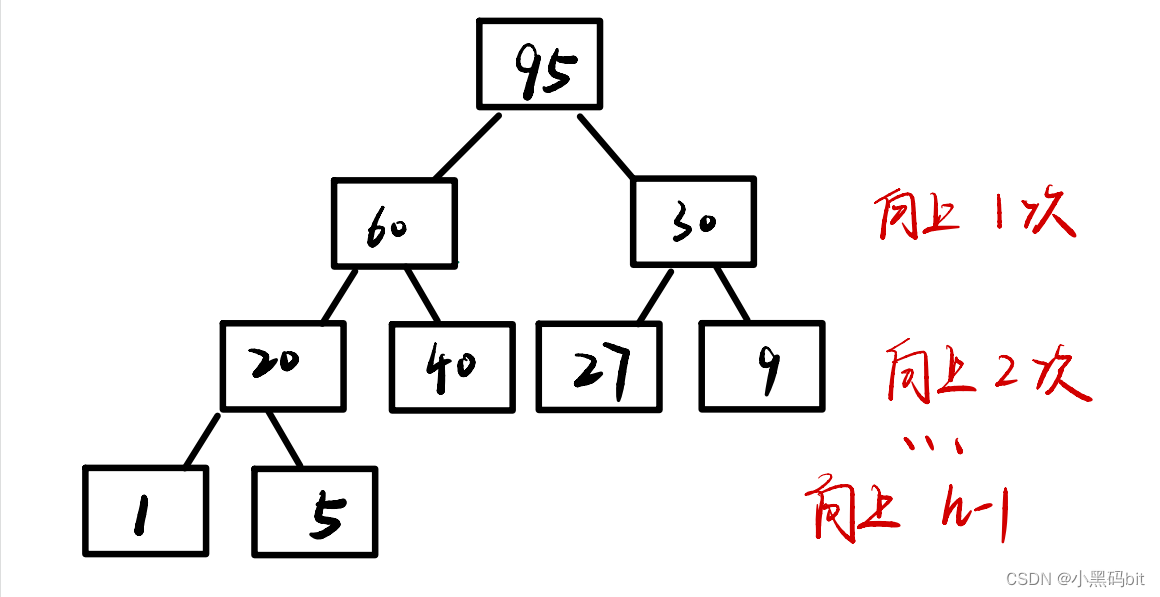
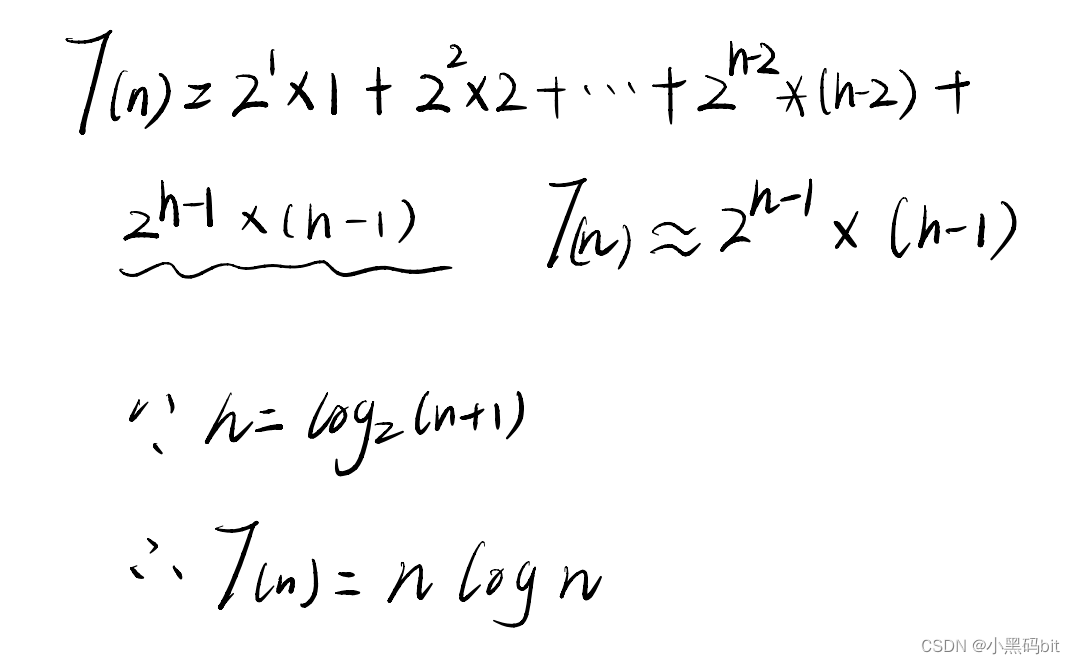
因此,当我们想要建堆的时候,我们优先选择向下调整建堆,他的时间代价更小。
问题引入:我们实现堆,是为了排序,那如果我们为了要升序序列,我们应该是怎样建堆?
7.堆排序的实现:
如果我们为了实现升序序列,我们应该建立大堆还是小堆?
应该是建立大堆
图解:
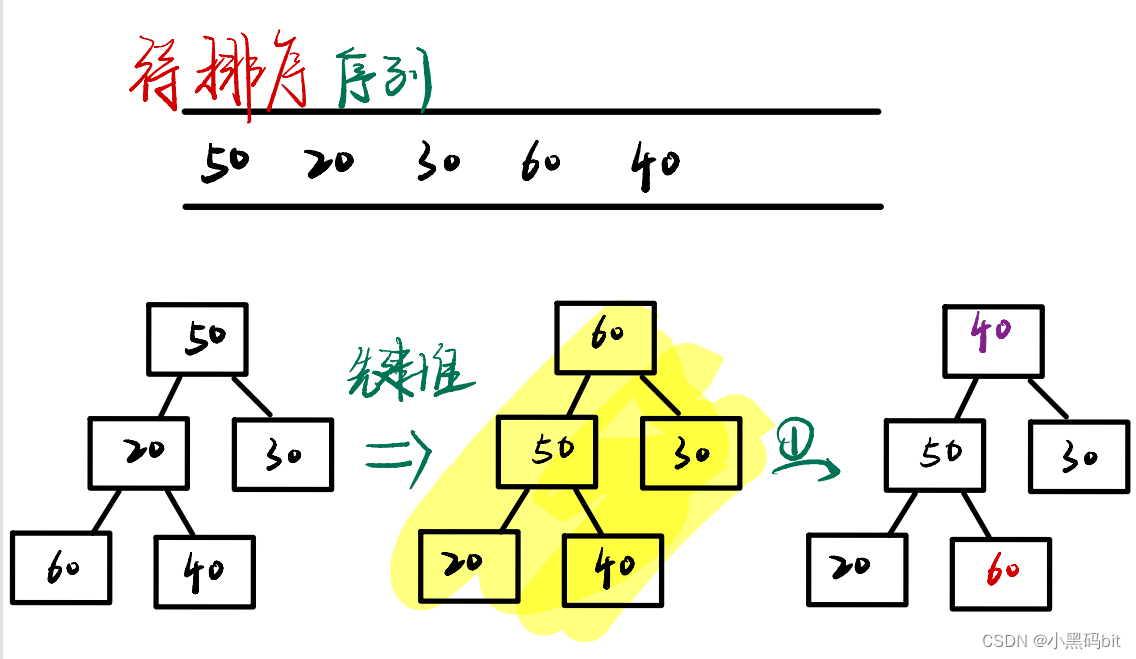
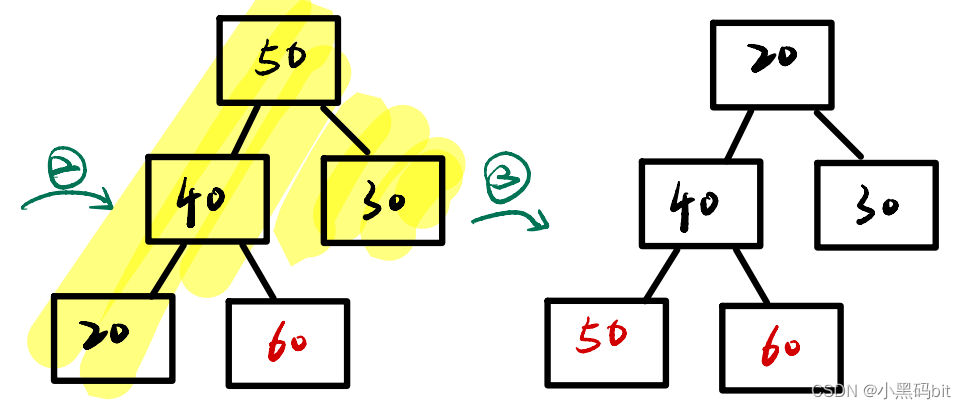
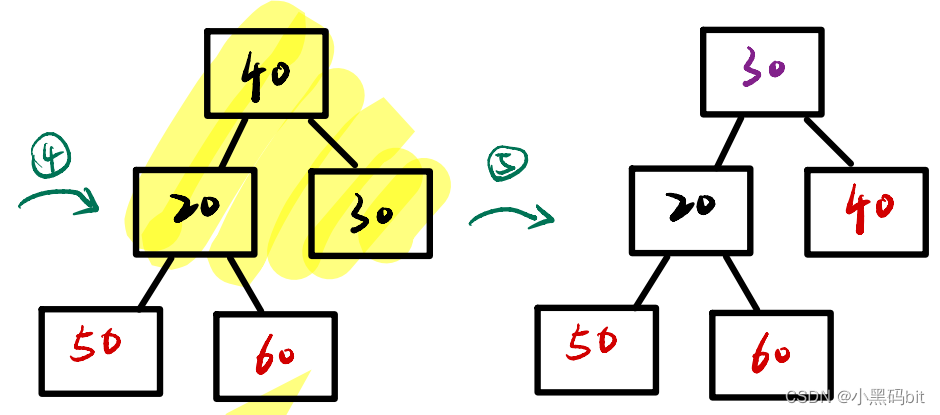
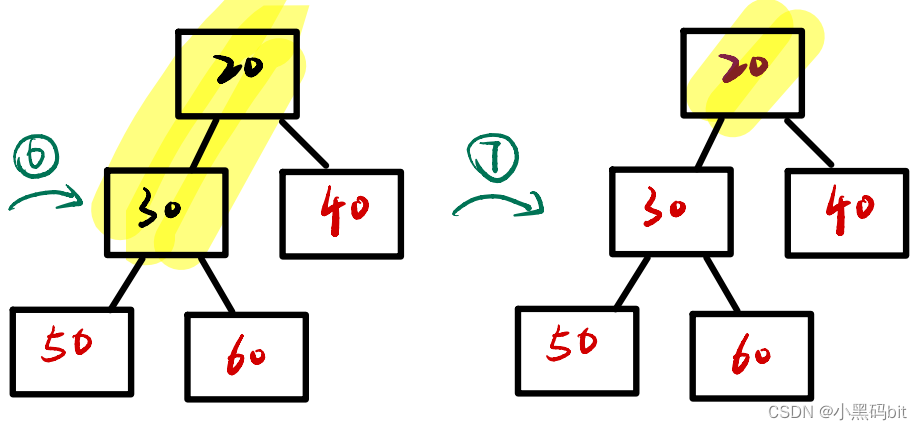
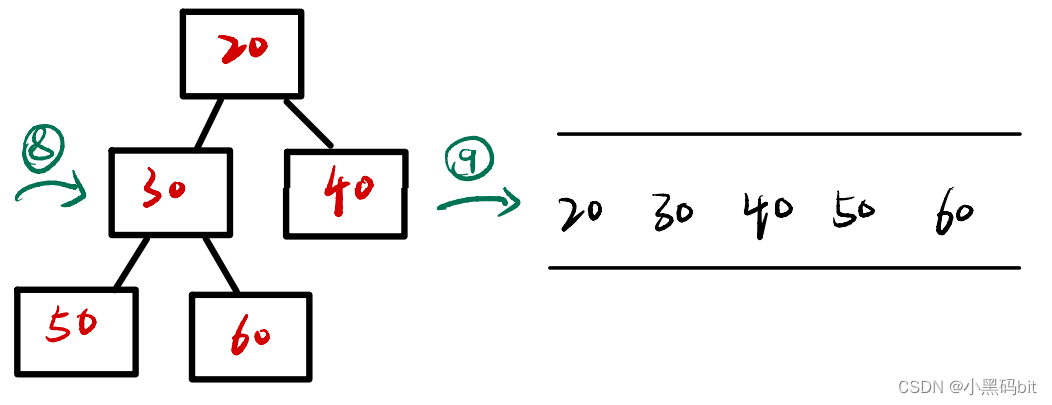
从图上我们可以看出,建立大堆的目的就是把最大的值,给放到数组的后面,也就是挑选出来,最后的数组里就是按升序排列的。当然我们要想实现降序序列,就是需要建立大根堆,将小的数挑选出来。
代码展示:
void HeapSort(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a, n, i);
}
// O(N*logN)
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
void Test3()
{
int array[] = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
HeapSort(array, sizeof(array) / sizeof(int));
for (int i = 0; i < sizeof(array) / sizeof(int); ++i)
{
printf("%d ", array[i]);
}
printf("\n");
}
堆排序的性能分析:
1.空间效率:
仅使用常数个辅助单元,空间复杂度为O(1)。
2.时间效率:
建堆的时间O(n),之后又向下调整操作n-1次,而完全二叉树的高度为 logN,最后平均时间复杂度为 O(N*logN)。



![[技术闲聊]我对电路设计的理解(三)](https://img-blog.csdnimg.cn/direct/45bdfbf399c248039631876127124fab.png)