Python | SLP | EOF | 去除季节趋势

前言

在计算EOF（经验正交函数）之前去除季节循环是为了消除数据中的季节变化的影响，使得EOF能够更好地捕捉数据中的空间变化模式。如果不去除季节循环，季节性信号可能会在EOF中占据较大的比例，从而影响对其他空间模态的识别。通过去除季节循环，我们可以更准确地识别和分析数据中的长期趋势和非季节性变化。

数据来源

monthly mean of surface pressure
2.5 ° x 2.5°
1948-01-01 ~ 2023-12-01
地址： http://apdrc.soest.hawaii.edu/las/v6/dataset?catitem=17027

<xarray.Dataset>
Dimensions:    (LON41_105: 65, LAT43_65: 23, TIME: 912, bnds: 2)
Coordinates:
  * LON41_105  (LON41_105) float64 100.0 102.5 105.0 107.5 ... 255.0 257.5 260.0
  * LAT43_65   (LAT43_65) float64 15.0 17.5 20.0 22.5 ... 62.5 65.0 67.5 70.0
  * TIME       (TIME) datetime64[ns] 1948-01-01 1948-02-01 ... 2023-12-01
Dimensions without coordinates: bnds
Data variables:
    TIME_bnds  (TIME, bnds) datetime64[ns] ...
    PRES       (TIME, LAT43_65, LON41_105) float32 ...
Attributes:
    history:      FERRET V6.5  31-Mar-24
    Conventions:  CF-1.0

基础概念

EOF（Empirical Orthogonal Function）：

EOF是一种用于分析空间场景的统计方法。它可以提取数据中的主要空间变化模式，即数据的主要空间结构。在EOF分析中，EOFs是空间模式，它们代表了数据在空间上的主要变化模式。通常，EOFs按照其对数据方差的贡献程度进行排序，因此，EOF1代表数据中的主要空间变化模式，EOF2代表次要的空间变化模式，依此类推。

EOFs通常是空间场景的正交函数，即它们之间是相互独立的。这意味着每个EOF捕获数据中不同的空间变化模式，不会出现重叠。

通过观察EOFs，可以了解数据中的主要空间结构，从而推断出数据的空间分布规律和特征。

PS ：个人理解EOF得到的第一模态，即在限定的空间区域内(比如说太平洋中部以及北部)，以及在这一限定时间周期内(比如说从1970-2010年内)，该空间区域内最显著、主导的空间 Pattern 。

PC（Principal Component）：

PC是EOF分析的另一个重要结果，它是每个时间步数据在EOF模式上的投影。换句话说，PC表示了数据随时间变化时，EOF空间模式的权重。 PC1通常表示数据中的主要时间变化模式，PC2表示次要的时间变化模式，以此类推。通常情况下，PC1会对应数据中的主要变化方向，即数据集的整体趋势或变化方向。

通过观察PC时间序列，可以了解数据在不同时间点上的变化规律，从而推断出数据的时间演变特征和趋势。

代码实现

from typing import Tuple
import os
import xarray as xr
import glob
import numpy as np
import cartopy.feature as cfeature
from cartopy.mpl.ticker import LongitudeFormatter, LatitudeFormatter
import cmaps
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import matplotlib.ticker as mticker
from eofs.standard import Eof
from matplotlib import ticker 
import cartopy.mpl.ticker              as ctk
# ================================================================================================
# Author: %(Jianpu)s | Affiliation: Hohai
# Email : %(email)s
# Last modified: 2024-04-03 12:28:06
# Filename: 
# Description: 
# =================================================================================================
# Your code continues here

定义读取nc文件函数


def read_netcdf(path: str, time_min: str, time_max: str) -> xr.Dataset:
    """
    读取NetCDF文件并返回数据集对象。

    参数:
    path (str): NetCDF文件的路径。
    time_min (str): 起始时间，格式为'YYYY-MM-DD'。
    time_max (str): 结束时间，格式为'YYYY-MM-DD'。

    返回值:
    data (xarray.Dataset): 包含选择时间范围内数据的数据集对象。
    """
    data = xr.open_dataset(path).sel(TIME=slice(time_min, time_max))
    return data

定义前处理函数，计算纬度权重、去除季节趋势、计算EOF和PC

计算纬度权重：

首先，通过 np.cos(np.deg2rad(lat)) 计算了每个纬度点的纬度值的余弦值，即 $cos(\text{纬度})$ 。然后，使用 np.sqrt(coslat) 对余弦值进行开方运算，得到了纬度权重。这样做的目的是因为地球在不同纬度上的面积并不相同，通过使用纬度权重，可以对数据进行加权，更准确地反映出不同纬度上的变化情况。

去除季节循环：

首先，获取数据的维度信息，包括时间维度（nt）、纬度维度（nlat）和经度维度（nlon）。然后，将数据按照时间、月份和网格点的顺序进行重塑，使得数据的形状变为 (月份, 年数, 网格点数)。接着，计算每个月份的平均值，得到了季节循环。然后，通过减去季节循环，得到了去除季节循环后的数据 pres_anom。这样做的目的是为了消除数据中的季节性变化，使得后续的EOF分析更加准确。

def preprocess_data(data: xr.Dataset) -> Tuple[np.ndarray, np.ndarray, np.ndarray, np.ndarray, np.ndarray]:
    """
    对数据进行预处理，包括计算纬度权重、去除季节循环等。

    参数:
    data (xarray.Dataset): 包含海平面气压数据的数据集对象。

    返回值:
    lon (numpy.ndarray): 经度数据。
    lat (numpy.ndarray): 纬度数据。
    eof (numpy.ndarray): EOF模态。
    pc (numpy.ndarray): PC时间序列。
    var (numpy.ndarray): 解释方差百分比。
    """
    lat = np.array(data.LAT43_65)
    lon = np.array(data.LON41_105)
    pres_data = data.PRES.data

    # 计算纬度权重
    coslat = np.cos(np.deg2rad(lat))
    wgts = np.sqrt(coslat)[..., np.newaxis]

    # 去除季节循环
    nt, nlat, nlon = pres_data.shape
    ngrd = nlon * nlat
    pres_ym = pres_data.reshape((12, round(nt / 12), ngrd), order='F').transpose((1, 0, 2))
    pres_clm = np.mean(pres_ym, axis=0)
    pres_anom = (pres_ym - pres_clm).transpose((1, 0, 2)).reshape((nt, nlat, nlon), order='F')
    # 计算EOF & PC
    solver = Eof(pres_anom, weights=wgts)
    eof = solver.eofsAsCorrelation(neofs=4)
    pc = solver.pcs(npcs=4, pcscaling=1)
    var = solver.varianceFraction(neigs=4)
    return lon, lat, eof, pc, var

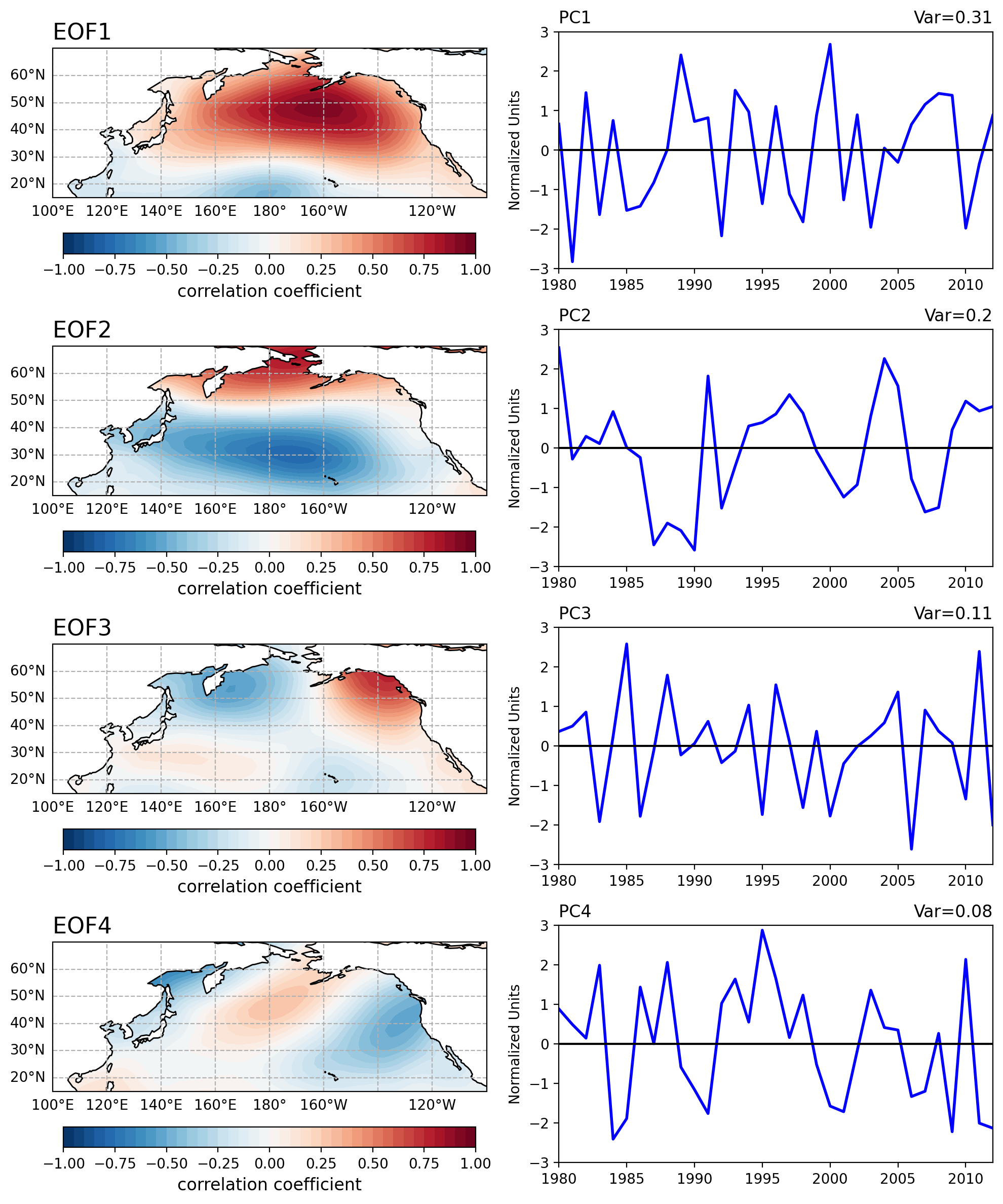
solver.eofsAsCorrelation(neofs=4)返回的是主要模态（leading EOF）与输入海表气压（SLP）之间的相关性。

pcscaling=1：表示对主成分时间序列进行缩放，使其具有单位方差。这意味着每个主成分的方差都被归一化为1，因此可以更容易地比较它们的相对重要性，等于0表示不缩放。

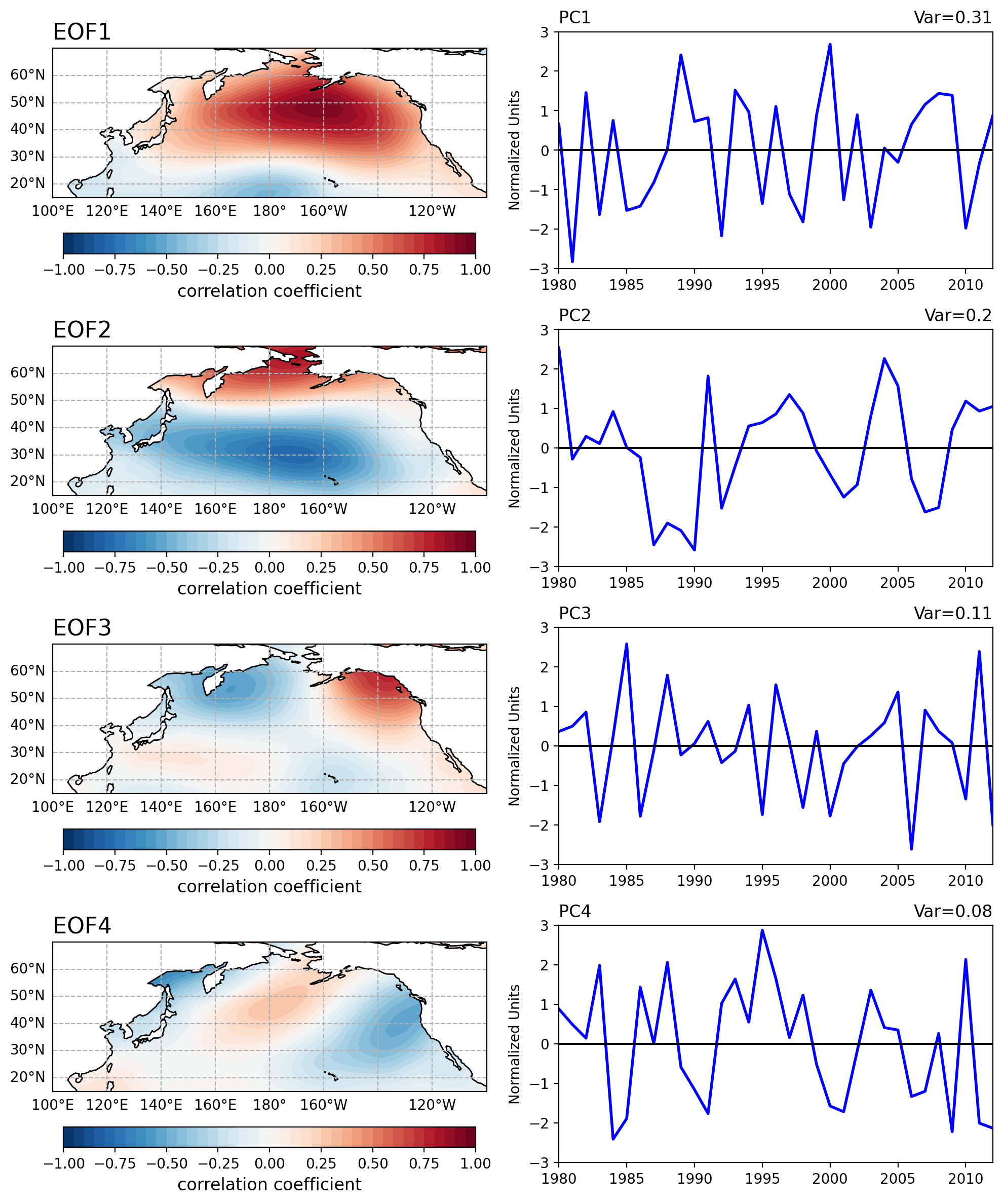
修改为solver.eofs(neofs=4)返回的是前4个EOF，即前4个空间模态。这些模态描述了数据集中的主要空间变化模式。

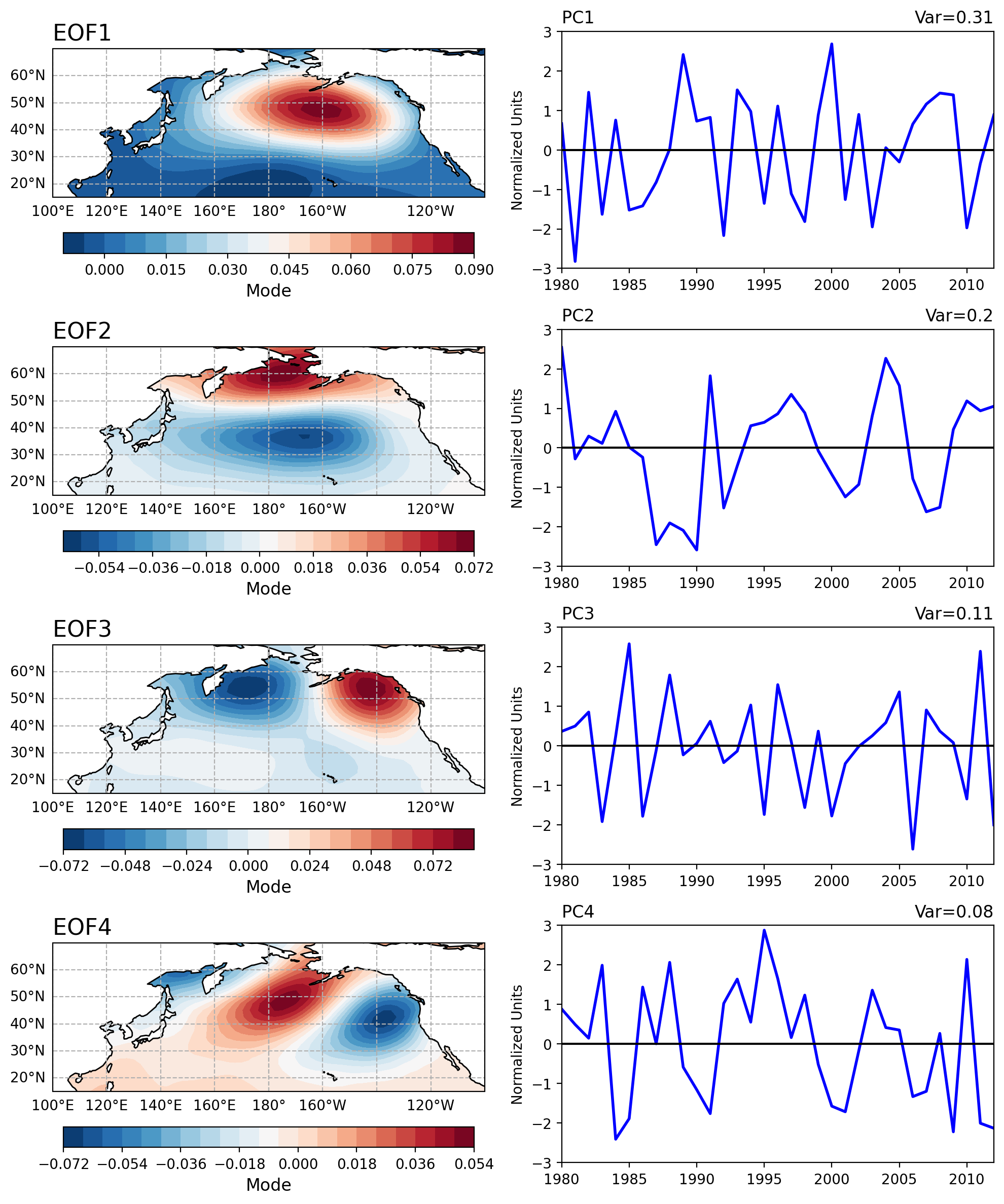
定义绘图函数，绘制EOF 和 PC 时间序列

这里绘制 PC 序列时，每12个数值绘制一个点，即每年一个数据

def plot_eof_and_pc(lons, lats, eof, pc, var,  ax1, ax2,EOF,PC):
    """
    绘制 EOF1 和 PC1 时间序列。

    参数:
    lons (numpy.ndarray): 经度数据，表示每个数据点的经度值。
    lats (numpy.ndarray): 纬度数据，表示每个数据点的纬度值。
    eof (numpy.ndarray): 表示 EOF1 的空间模式，表示每个数据点的 EOF1 值。
    pc (numpy.ndarray): 表示 PC1 的时间序列，表示每个时间步的 PC1 值。
    var (float): 表示 EOF1 解释的方差百分比，表示 EOF1 解释的总方差的百分比。
    season (str): 当前季节的字符串表示，用于图表标题。
    ax1 (matplotlib.axes.Axes): 第一个子图的轴对象，带有投影，用于绘制 EOF1 空间模式。
    ax2 (matplotlib.axes.Axes): 第二个子图的轴对象，不带投影，用于绘制 PC1 时间序列。
    """
    clevs = np.linspace(-1, 1, 41)
    
    fill = ax1.contourf(lons, lats, eof.squeeze(), clevs,
                        transform=ccrs.PlateCarree(), cmap=plt.cm.RdBu_r)
    ax1.add_feature(cfeature.LAND, facecolor='w', edgecolor='k', zorder=1)
    cb = plt.colorbar(fill, ax=ax1,  
                       orientation ='horizontal',
                      shrink=0.75
                     )
    cb.set_label('correlation coefficient', fontsize=12)
    ax1.set_title(f'{EOF}  ', fontsize=16,loc='left')
    gl = ax1.gridlines(draw_labels=True, x_inline=False, y_inline=False, linestyle='dashed')
    gl.top_labels = False
    gl.right_labels = False
    gl.rotate_labels = False
    gl.xlocator = ctk.LongitudeLocator(20)
    gl.ylocator = ctk.LatitudeLocator(8)
    gl.xformatter = ctk.LongitudeFormatter(zero_direction_label=True)
    gl.yformatter = ctk.LatitudeFormatter()

    years = range(int(time_min),int(time_max)+1)
    ax2.plot(years, pc[::12], color='b', linewidth=2)
    ax2.axhline(0, color='k')
    ax2.set_title(f'{PC}  ',loc='left')
    # ax2.set_xlabel('Year')
    ax2.set_ylabel('Normalized Units')
    ax2.set_xlim(int(time_min),int(time_max))
    ax2.set_ylim(-3, 3)
    ax2.set_title(f'Var={var:.2}', loc='right')

主程序：循环绘图

path = r'G:/code_daily/slp.nc'
time_min,time_max = '1980','2012'
data = read_netcdf(path,time_min,time_max)

# 数据预处理
lon, lat, eof, pc,var = preprocess_data(data)

# 绘制 EOF 和 PC
fig = plt.figure(figsize=(10, 12),dpi=600)

EOFs = ['EOF1', 'EOF2','EOF3','EOF4',]
PCs = ['PC1', 'PC2','PC3','PC4']

for i, EOF in enumerate(EOFs):
    
    print(i,EOF,)
    
    # 第一个子图带投影
    ax1 = fig.add_subplot(4, 2, 2*i+1, projection=ccrs.PlateCarree(central_longitude=180))
    # 第二个子图不带投影
    ax2 = fig.add_subplot(4, 2, 2*i+2)
    plot_eof_and_pc(lon, lat, eof[i], pc[:,i], var[i], ax1, ax2,EOFs[i],PCs[i])
plt.tight_layout()
plt.show()