原内容请参考哈尔滨工业大学何飞教授：https://www.bilibili.com/video/BV18b4y1Y7wd/?p=12&spm_id_from=pageDriver&vd_source=61654d4a6e8d7941436149dd99026962
或《材料物理性能及其在材料研究中的应用》（哈尔滨工业大学出版社）
离子扩散
离子类载流子导电是离子类载流子在电场作用下，通过材料的长距离的迁移。从理论上讲，离子导电需要从离子扩散（移动）的角度出发进行考虑。
导电性离子的特点
- 离子半径较小，电价低的离子，在晶格内的键型主要是离子键。由于离子之间的库仑力较小，故容易发生迁移。
- 可移动的阳离子：H+、NH4+、Li+、Na+、K+、Rb+、Cu+、Ag+、Ga+、Tl+等。
- 可移动的阴离子：O2-、F-、Cl-等。
离子的导电能力可用离子的电导率关系进行评估：
σ
=
n
q
μ
\sigma=nq\mu
σ=nqμ
离子电导率关系表达式
σ
=
n
q
μ
\sigma=nq\mu
σ=nqμ
载流子浓度 n n n
- 对于本征电导，载流子由晶体本身的热缺陷提供（包括：弗伦克尔缺陷和肖特基缺陷）。
弗伦克尔缺陷：离子脱离（格点）平衡位置挤入晶体间隙，先占据的格点处留下一个空位。这种缺陷的特点是间隙离子和空位是成对出现的；
肖特基缺陷：由于热运动，晶体中阳离子及阴离子脱离平衡位置，跑到晶体表面或晶界位置上，从而形成一层新的界面而产生阳离子空位以及阴离子空位。 - 热缺陷浓度表达式：
{ N f = N exp ( − E f 2 k B T ) N s = N exp ( − E s 2 k B T ) \left\{\begin{array}{l} N_{\mathrm{f}}=N \exp \left(\frac{-E_{\mathrm{f}}}{2 k_{\mathrm{B}} T}\right) \\ N_{\mathrm{s}}=N \exp \left(\frac{-E_{\mathrm{s}}}{2 k_{\mathrm{B}} T}\right) \end{array}\right. ⎩ ⎨ ⎧Nf=Nexp(2kBT−Ef)Ns=Nexp(2kBT−Es)- N f N_{\mathrm{f}} Nf：弗伦克尔缺陷浓度
- N s N_{\mathrm{s}} Ns：肖特基缺陷浓度
- N N N：单位体积内的离子结点数
- E f E_{\text{f}} Ef：形成一个弗伦克尔缺陷所需要的能量（离解能）
- E s E_{\mathrm{s}} Es：形成一个肖特基缺陷所需要的能量（离解能）
（1）热缺陷浓度取决于温度和离解能；
（2）常温条件下，
k
B
T
<
<
E
k_BT<<E
kBT<<E，只有在高温下，热缺陷浓度才显著，即本征电导在高温下显著。
（3）离解能越大，产生热缺陷的难度越大，形成的热缺陷浓度越低。
（4）一般来说，肖特基缺陷形成能比弗伦克尔缺陷形成能低很多。只有在结构很松散，离子半径很小的情况下，才容易形成弗伦克尔缺陷。
（5）杂质离子载流子的浓度取决于杂质的数量和种类。低温条件下离子晶体的电导主要由杂质载流子浓度所决定，杂质离子的存在不仅增加了电流载流子数，而且使点阵发生畸变，杂质离子的离解活化能变小。
离子迁移
迁移率是指单位电场强度下载流子的迁移速度。对离子导电来说是离子电荷载流子在电场作用下通过材料的长距离的迁移，热运动能是间隙离子迁移所需要的能量的主要来源。
离子迁移原理
假设一个间隙离子位于间隙位置，受周围离子的影响，处于一定的平衡位置。该位置处隔离子间距
δ
\delta
δ的一半的位置处称为半稳定位置。
如果间隙离子由于热运动穿过势垒
U
0
U_0
U0，从一个间隙位置进入另一个相邻原子的间隙位置，那么就实现了离子迁移。迁移的距离刚好为离子间距
δ
\delta
δ。
间隙离子单位时间沿某一方向跃迁的次数 P P P
一个间隙离子由于热运动，越过势垒
U
0
U_0
U0跃迁至邻近间隙位置，根据玻尔兹曼统计规律，单位时间沿某一方向跃迁的次数为：
P
=
γ
0
6
exp
(
−
U
0
k
B
T
)
P=\frac{\gamma_0}{6}\exp(-\frac{U_0}{k_BT})
P=6γ0exp(−kBTU0)（阿伦尼乌兹方程形式）
其中，
γ
0
\gamma_0
γ0是间隙离子在半稳定位置处的振动频率。
小结：
（1）迁移次数与温度有关，温度越高，迁移次数越多；
（2）迁移次数主要受势垒
U
0
U_0
U0的影响，
U
0
U_0
U0越高，迁移次数越少。
无外加电场时离子迁移为什么不导电
无外加电场时，间隙离子在晶体中各个方向的迁移次数都相同，宏观上无电荷定向运动，因此不导电。
外加电场条件下的离子迁移
加上电场后，晶体间隙离子的势垒不再对称。此时电荷数为
q
q
q的正间隙离子受到的电场力
F
=
q
E
F=qE
F=qE与电场
E
E
E的方向一致，则电场
E
E
E在
δ
/
2
\delta/2
δ/2距离上的位势差为：
Δ
U
=
F
⋅
δ
2
=
q
E
⋅
δ
2
\Delta U=F\cdot\frac{\delta}{2}=qE\cdot\frac{\delta}{2}
ΔU=F⋅2δ=qE⋅2δ
顺/逆电场方向间隙离子单位时间内跃迁的次数
{
P
+
=
γ
0
6
exp
(
−
U
0
−
Δ
U
k
B
T
)
P
−
=
γ
0
6
exp
(
−
U
0
+
Δ
U
k
B
T
)
\left\{ \begin{array}{l} P^+=\frac{\gamma_0}{6}\exp(-\frac{U_0-\Delta U}{k_BT}) \\ P^-=\frac{\gamma_0}{6}\exp(-\frac{U_0+\Delta U}{k_BT}) \end{array}\right.
{P+=6γ0exp(−kBTU0−ΔU)P−=6γ0exp(−kBTU0+ΔU)
由于指向右侧电场
E
E
E的存在，使离子更容易向右侧移动，造成势场
U
0
U_0
U0发生不对称变化。
剩余迁移次数
Δ
P
=
P
+
−
P
−
\Delta P=P^+-P^-
ΔP=P+−P−
（离子）载流子沿电场方向的迁移速度
由于间隙离子每跃迁一次的距离为离子间距
δ
\delta
δ，因此载流子沿电场方向的跃迁速度为：
v
=
Δ
P
⋅
δ
=
γ
0
6
exp
(
−
U
0
k
B
T
)
[
exp
(
Δ
U
k
B
T
)
−
exp
(
−
Δ
U
k
B
T
)
]
⋅
δ
v=\Delta P\cdot\delta=\frac{\gamma_0}{6}\exp(-\frac{U_0}{k_BT})[\exp(\frac{\Delta U}{k_BT})-\exp(-\frac{\Delta U}{k_BT})]\cdot \delta
v=ΔP⋅δ=6γ0exp(−kBTU0)[exp(kBTΔU)−exp(−kBTΔU)]⋅δ
小电场下的近似处理
由于
e
x
−
1
e^x-1
ex−1的等价无穷小为
x
x
x，因此当电场不大时，
Δ
U
<
<
k
B
T
\Delta U<<k_BT
ΔU<<kBT，故可作如下近似：
{
exp
(
Δ
U
k
B
T
)
≈
1
+
Δ
U
k
B
T
exp
(
−
Δ
U
k
B
T
)
=
1
−
Δ
U
k
B
T
\left\{ \begin{array}{l} \exp(\frac{\Delta U}{k_BT})\approx 1+\frac{\Delta U}{k_BT} \\\exp(-\frac{\Delta U}{k_BT})=1-\frac{\Delta U}{k_BT} \end{array} \right.
{exp(kBTΔU)≈1+kBTΔUexp(−kBTΔU)=1−kBTΔU
将位势差
Δ
U
=
q
E
⋅
δ
2
\Delta U=qE\cdot \frac{\delta}{2}
ΔU=qE⋅2δ代入可得：
v
=
E
⋅
δ
2
γ
0
q
6
k
B
T
exp
(
−
U
0
k
B
T
)
v=E\cdot\frac{\delta^2\gamma_0 q}{6k_BT}\exp(-\frac{U_0}{k_BT})
v=E⋅6kBTδ2γ0qexp(−kBTU0)（外加电场不大时，离子沿电场方向迁移速度的近似方程）
由于迁移率是单位电场强度下载流子的迁移速度，因此当外加电场不大时，离子载流子沿电场方向的迁移率可近似表示为：
μ
=
v
E
=
δ
2
γ
0
q
6
k
B
T
exp
(
−
U
0
k
B
T
)
\mu=\frac{v}{E}=\frac{\delta^2\gamma_0 q}{6k_BT}\exp(-\frac{U_0}{k_BT})
μ=Ev=6kBTδ2γ0qexp(−kBTU0)
离子电导率
载流子浓度及迁移率确认以后，离子载流子的电导率可以按电导率的关系 σ = n q μ \sigma=nq\mu σ=nqμ来确定。如果本征导电由肖特基缺陷引起，则离子电导率为 σ = N s q μ \sigma=N_{\mathrm{s}}q\mu σ=Nsqμ，其中：
- 离子迁移率： μ = v E = δ 2 γ 0 q 6 k B T exp ( − U 0 k B T ) \mu=\frac{v}{E}=\frac{\delta^2\gamma_0 q}{6k_BT}\exp(-\frac{U_0}{k_BT}) μ=Ev=6kBTδ2γ0qexp(−kBTU0)
- 离子载流子浓度： N s = N exp ( − E s k B T ) N_{\mathrm{s}}=N\exp(-\frac{E_{\mathrm{s}}}{k_BT}) Ns=Nexp(−kBTEs)
代入电导率关系式可得，离子载流子的电导率表达式为：
σ
=
N
⋅
δ
2
q
2
γ
0
6
k
B
T
⋅
exp
[
−
(
U
s
+
1
2
E
s
k
B
T
)
]
=
A
s
exp
(
−
W
s
k
B
T
)
\sigma=N\cdot \frac{\delta^2q^2\gamma_0}{6k_BT}\cdot\exp[-(\frac{U_{\mathrm{s}}+\frac{1}{2}E_{\mathrm{s}}}{k_BT})]=A_{\mathrm{s}}\exp(-\frac{W_{\mathrm{s}}}{k_BT})
σ=N⋅6kBTδ2q2γ0⋅exp[−(kBTUs+21Es)]=Asexp(−kBTWs)
其中，
A
s
A_{\mathrm{s}}
As在温度不高的范围内为常数。
W
s
=
U
s
+
1
2
E
s
W_{\mathrm{s}}=U_{\mathrm{s}}+\frac{1}{2}E_{\mathrm{s}}
Ws=Us+21Es为电导活化能，包括缺陷形成能
E
s
E_{\mathrm{s}}
Es和迁移能
U
s
U_{\mathrm{s}}
Us。
从电导活化能可以分析出，要实现离子导电，材料自身首先需要克服势垒，也就是克服缺陷形成能
E
s
E_{s}
Es形成热缺陷，然后再克服热缺陷的迁移能
U
s
U_s
Us，才能实现离子的迁移。因此电导率主要是指数部分来决定的。
离子电导率与温度的半对数关系
令
B
s
=
W
s
k
B
B_s=\frac{W_s}{k_B}
Bs=kBWs，则
σ
=
A
s
exp
(
−
W
s
k
B
T
)
=
A
s
exp
(
−
B
s
T
)
\sigma=A_s\exp(-\frac{W_s}{k_BT})=A_s\exp(-\frac{B_s}{T})
σ=Asexp(−kBTWs)=Asexp(−TBs)
⇒
ln
σ
=
A
1
−
B
s
T
\Rightarrow \ln\sigma=A_1-\frac{B_s}{T}
⇒lnσ=A1−TBs（对数形式）
从上式可以看出，离子迁移的载流子电导率与温度呈半对数线性规律。
*电阻率与温度的半对数线性关系可表示为：
ln
ρ
=
A
2
+
W
s
T
\ln\rho=A_2+\frac{W_s}{T}
lnρ=A2+TWs
半对数关系的意义
以
ln
σ
\ln\sigma
lnσ为Y轴，以
1
T
\frac{1}{T}
T1为X轴，可从拟合直线的斜率来求得电导活化能
W
s
W_s
Ws.
多种（离子类）载流子参与导电的情况
如果有多种（离子类）载流子参与导电，则总电导率为：
σ
i
=
∑
i
A
i
exp
(
−
B
i
T
)
\sigma_i=\sum_{i}{A_i\exp(-\frac{B_i}{T})}
σi=∑iAiexp(−TBi)，并且不论本征导电还是杂质导电，均可仿照这个式子的形式写出。
影响离子导电的因素
温度的影响
- 半对数线性规律：
ln
σ
=
A
1
−
B
s
T
\ln\sigma=A_1-\frac{B_s}{T}
lnσ=A1−TBs
温度升高，电导率将以指数形式增加。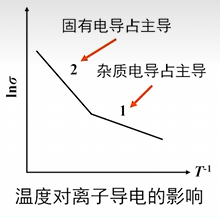
随着温度的增加，电导率总体呈线性增加。从细节上看，电阻率对数的斜率，即电导活化能会发生变化而出现拐点，原因是由于低温下杂质电导占主导，但随着温度的升高，热运动能量增高，本征导电的载流子增多，从而转为由本征导电逐渐占主导。由于导电方式由杂质导电逐渐变为本征导电，并且杂质活化能较点阵离子的活化能低，因此会出现电导率半对数关系的拐点。另外，对数陶瓷材料而言，这一拐点的出现还可能跟导电机制的改变有关（b）。因此半对数线性规律出现拐点需要具体问题具体分析：
- 导电机构变化。对于多数陶瓷，低温为杂质导电，高温为本征导电。
- 导电载流子种类发生变化。例如，刚玉，低温为杂质离子导电，高温为电子导电。
半对数线性规律性是离子导体的电阻分析基本规律，也是研究离子迁移热力学参数一种便捷、重要的手段。
离子性质、晶体结构的影响
- 离子性质、晶体结构对离子导电的影响是通过改变电导活化能 W s W_s Ws实现的。
① 熔点高的离子
原子间结合力大，电导活化能高，电导率低；
② 离子半径
负离子半径增大（原子间结合力减弱），正离子活化能降低，电导率增大。
*这也解释了碱卤化合物中随着负离子的增加，电导活化能逐渐减弱，电导率更强。（例如：NaI导电性强于NaCl）
高价正离子，化合价越大（价键强，活化能高），扩散激活能增大（迁移率降低），则电导率降低。
③ 晶体结构
晶体结构间隙越大，离子越容易运动（活化能越小），电导率越大。
点缺陷对离子导电的影响
离子晶体中点缺陷的生成和浓度的大小是决定离子导电的关键。
- 影响点缺陷的形成和浓度大小的因素：
① 热激励生成晶体缺陷
理想晶体中离子不能脱离点阵位置而移动。当晶体受到热激励时会产生弗伦克尔缺陷和肖特基缺陷，其中肖特基缺陷更容易产生，从而导致离子脱离点阵而留下空位形成晶体缺陷。
② 不等价固溶掺杂形成晶体缺陷
例如，二价铬离子（Cd2+）进入由一价银离子(Ag+)组成的AgBr的晶格中，Cd2+更容易取代Ag+，从而形成晶格缺陷。
③ 环境气氛发生变化，引起正负离子化学计量比改变，生成晶格缺陷。
例如，稳定型ZrO2由于氧的脱离而形成氧空位。
对离子类载流子与电子类载流子的导电分析认识
离子类载流子导电
（离子类载流子导电→离子迁移→扩散→电导率）
离子类载流子导电，离子迁移是离子导电的关键，所以我们需要从离子迁移难易程度的角度去分析离子导电的问题，这本质上是涉及到离子的扩散问题，也就是说，利用电导率作为评价离子迁移难易程度的物理量更加合适。
电子类载流子导电
（电子类载流子导电→电子散射→阻碍→电阻率）
电子类载流子导电，电子运动时发生散射，使电子运动受到阻碍，从这个角度考虑，用电阻率作为评价电子导电的物理量更为合适。
离子导电与离子扩散之间的关系
- 离子导电：离子在电场作用下定向迁移的现象。
离子扩散的三种机制
- 空位扩散：
以空位作为媒介进行的扩散，空位周围相邻的原子或离子跃入空位，该离子原来占有的点阵格点位置变成空位，这个新的空位周围的离子再跃入这个空位，以此实现离子的扩散。
由于空位的存在，使周围邻近离子跳入空位所需的势垒较低，因此以此方式实现的扩散较为容易。
- 间隙扩散：
扩散的离子或原子在晶格间隙的位置之间的运动，此时离子从一个间隙位置到达相邻间隙位置时，必须把点阵上间隙离子周围点阵上的离子挤开，使晶格发生局部的瞬时畸变，这部分畸变能便是离子扩散时所必须克服的势垒，因此间隙扩散往往较难进行。
- 填隙扩散：
在填隙机制中，两个离子或原子同时移位运动，其中一个是间隙离子，另一个是处于点阵上的离子。间隙离子取代附近点阵上的离子进入点阵位置，而被取代的点阵离子则进入间隙位置。
这种扩散运动由于晶格变形小，因此也比较容易产生。
扩散系数 D D D和电导率 σ \sigma σ之间的关系
- 扩散激活能：离子扩散时，需要克服势垒的阻碍，这一能量称为扩散激活能。
扩散系数 D D D随温度的变化关系
D = D 0 exp ( − W R T ) D=D_0\exp(-\frac{W}{RT}) D=D0exp(−RTW)
- D 0 D_0 D0：扩散常数
- R R R：气体常数
- W W W：扩散激活能
*扩散系数
D
D
D可由实验所测得，结合温度与扩散系数的关系，上式两侧取对数后得到半对数线性关系：
ln
D
=
ln
D
0
−
W
R
T
\ln D=\ln D_0 -\frac{W}{RT}
lnD=lnD0−RTW
能斯特-爱因斯坦方程
Nernst-Einstein方程建立了扩散系数
D
D
D与电导率
σ
\sigma
σ之间的关系：
σ
=
D
⋅
n
q
2
k
B
T
\sigma=D\cdot\frac{nq^2}{k_BT}
σ=D⋅kBTnq2
- n n n：离子载流子浓度
- q q q：离子电荷量
这个方程式从扩散第一定律出发，结合电导率的关系推出。
式中的
n
,
q
,
k
B
n,q,k_B
n,q,kB对于具体的材料而言是固定的，因此电导率与扩散系数之间是呈正比的。
根据电导率的关系式
σ
=
n
q
μ
\sigma=nq\mu
σ=nqμ，并结合能斯特-爱因斯坦方程，可建立扩散系数和离子迁移率之间的关系：
D
=
μ
q
k
B
T
=
B
k
B
T
D=\frac{\mu}{q}k_BT=Bk_BT
D=qμkBT=BkBT
其中，
B
=
μ
q
B=\frac{\mu}{q}
B=qμ称为离子绝对迁移率。
![练习 19 Web [BJDCTF2020]Easy MD5](https://img-blog.csdnimg.cn/direct/7e899c0de4fe40f4a663165aaa1e0299.png)
![[每周一更]-第92期：Go项目中的限流算法](https://img-blog.csdnimg.cn/direct/8d3db66f0eaa408591da7acccaa5dd49.png#pic_center)
