LC 144.二叉树的前序遍历

news2024/11/17 4:39:55

二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：

输入： root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入： root = []
输出：[]

示例 3：

输入： root = [1]
输出：[1]

示例 4：

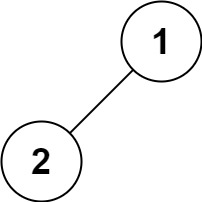
输入： root = [1,2]
输出：[1,2]

示例 5：

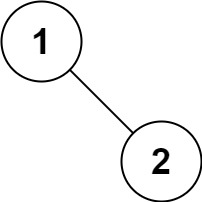
输入： root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
$\leq Node.val \leq 100$

进阶： 递归算法很简单，你可以通过迭代算法完成吗？

解法一(递归)

思路分析：

首先确定使用递归的方式实现前序遍历，然后需要思考如何实现递归，一般思考三点：
即先确定函数的参数和返回值，因为需要获取二叉树节点值，并得到一个列表，所以参数中需要有二叉树的节点和一个用来存储节点值的列表，此外不需要其他参数，然后也不需要返回值，将节点值保存到列表中即可
确定递归的终止条件，因为使用的是前序遍历，深度优先搜索，所以需要先往深处遍历二叉树，即递归终止条件为：节点为空，则说明深处遍历结束，继续换另外一条分支遍历。
最后确定递归的过程，题目要求前序遍历二叉树，因此先遍历父节点，然后再遍历左节点，最后遍历右节点，所以递归中；先保存当前节点值，然后调用递归函数先传递左节点再传递右节点

实现代码如下：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        preorderTraversal(root, ans);
        return ans;
    }
    private void preorderTraversal(TreeNode node, List<Integer> ans) {
        if (node == null)
            return ;    // 递归终止条件
        // 递归过程
        ans.add(node.val);    // 先遍历父节点
        preorderTraversal(node.left, ans);    // 再遍历左子节点
        preorderTraversal(node.right, ans);    // 最后遍历右子节点
    }
}

提交结果如下：

解答成功:
执行耗时:0 ms,击败了100.00% 的Java用户
内存消耗:40.4 MB,击败了5.37% 的Java用户

复杂度分析：

时间复杂度： $O (n)$ ，遍历一遍二叉树
空间复杂度： $O (n)$ ，考虑递归函数的调用

解法二(迭代栈)

思路分析：

根据栈和递归的关系，对于该题可以使用栈来完成二叉树的前序遍历，即应首先思考栈中应该保存什么，因为我们遍历的二叉树，所以栈中应该存储二叉树的节点
对于迭代，先思考迭代的过程，前序遍历的顺序是中左右，因此迭代中，首先要遍历到中节点，然后再遍历左右
所以，在迭代前，应先将根节点保存到栈中，然后才能在迭代中先获取中间节点，然后再继续遍历左右节点，根据栈先进后出的规律，所以先将右节点保存到栈中，再将左节点保存到栈中，如此，在下一轮迭代前，先出来遍历的则是左节点
同时对于迭代的退出条件，既然用栈来存放二叉树的节点，则当栈为空时，说明已经遍历完二叉树，所以栈为空时，退出循环

实现代码如下：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();

        if (root == null)    // 边界条件
            return ans;

        Deque<TreeNode> stack = new LinkedList<>();    // 用于存储二叉树的节点
        stack.push(root);
        while (!stack.isEmpty()) {
            // 前序遍历先遍历 中
            TreeNode node = stack.pop();
            ans.add(node.val);
            // 根据栈后进先出 先保存右节点
            if (node.right != null)
                stack.push(node.right);
            // 再保存左节点
            if (node.left != null)
                stack.push(node.left);
        }
        return ans;
    }
}

提交结果如下：

解答成功:
执行耗时:0 ms,击败了100.00% 的Java用户
内存消耗:40.1 MB,击败了10.31% 的Java用户

复杂度分析：

时间复杂度： $O (n)$ ，遍历整个二叉树
空间复杂度： $O (n)$ ，使用栈来辅助遍历二叉树

解法三(统一迭代法)

思路分析：

对于将要访问的节点和将要处理的节点均放入栈中
但是使用空指针来对将要处理的节点进行标记
本质上，即使将栈中元素顺序以前序遍历顺序输出

实现代码如下：

class Solution {
    // 统一迭代法 后序
	public List<Integer> preorderTraversal(TreeNode root) {
		List<Integer> ans = new ArrayList<>();
		if (root == null)	// 边界条件
			return ans;
		Deque<TreeNode> stack = new LinkedList<>();	// 用于存储二叉树的节点
		stack.push(root);
		while (!stack.isEmpty()) {
			TreeNode node = stack.pop();
			if (node != null) {
				// 前序遍历 先保存右节点
				if (node.right != null)
					stack.push(node.right);
				// 再保存左节点
				if (node.left != null)
					stack.push(node.left);
				// 最后 中节点入栈
				stack.push(node);
				stack.push(null);	// 空指针进行标记
			} else {
				node = stack.pop();
				ans.add(node.val);
			}
		}
		return ans;
		}
		}
		return ans;
	}
}