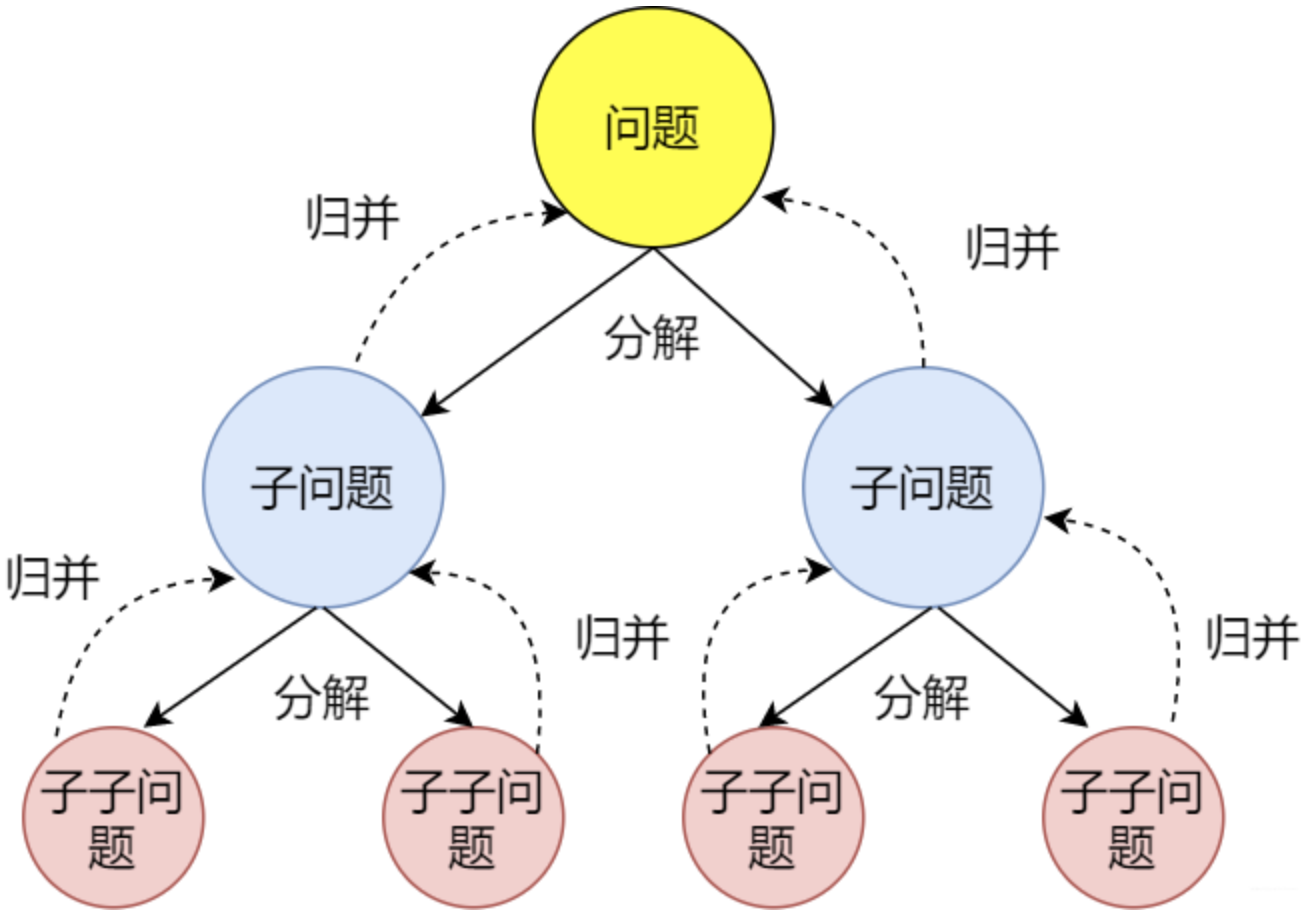
分治核心思想:
- 分解(Divide):将原问题分解成一系列子问题。这些子问题应该是原问题的较小版本。
- 解决(Conquer):递归地解决这些子问题。如果子问题的规模足够小,则直接求解。
- 合并(Combine):将子问题的解合并起来,形成原问题的解。
逆序对问题中:
- 分解:只要数组长度超过1,就不断均分数组
- 解决:当数组长度为1或0时,数组有序 且 没有逆序对 ✅
- 合并:当前数组分成左右两部分,总逆序对数量 = i,j都在左边的逆序对数量 + i,j都在右边的逆序对数量 + i在左边,j在右边的逆序对数量
故解法如下:
func mSort(arr []int) ([]int, int) { // 分治思想
if len(arr) <= 1 { // 只要长度超过1就继续分
return arr, 0
}
mid := len(arr) / 2
left, right := arr[:mid], arr[mid:]
arr1, cnt1 := mSort(left) // i,j都在左边的逆序对数量
arr2, cnt2 := mSort(right) // i,j都在右边的逆序对数量
newArr, cnt3 := merge(arr1, arr2) // i在左边,j在右边的逆序对数量
return newArr, cnt1 + cnt2 + cnt3
}
func merge(left, right []int) (newArr []int, count int) {
m, n := len(left), len(right)
newArr = make([]int, m+n)
var i, j int
for i < m && j < n {
if left[i] <= right[j] { // right[j] 没有 对应的 逆序对
newArr[i+j] = left[i]
i++
} else {
count += m - i // right[j]与每一个left[i] 都形成一个 逆序对
newArr[i+j] = right[j]
j++
}
}
for i < m { // 剩余元素加到末尾
newArr[i+j] = left[i]
i++
}
for j < n {
newArr[i+j] = right[j]
j++
}
return newArr, count
}
func reversePairs(record []int) int {
_, cnt := mSort(record)
return cnt
}
更多分治问题:
1> 构造类型,奇偶分治,位分治
| 题目 | 说明 | 实现 |
|---|---|---|
| 932. 漂亮数组 | 题意即两数之和不能为偶数,故数组分为偶数部分和奇数部分,因为 偶数 + 奇数 != 偶数 | 我的提交 |
| 1238. 循环码排列 | 先不考虑start,按最高位为0、1将数据分为左右部分构造,后面再循环移动至start到0位置处 | 我的提交 |
2> 分治构造
| 题目 | 说明 | 实现 |
|---|---|---|
| 889. 根据前序和后序遍历构造二叉树 | 通过前序找到根节点,从而划分后序遍历为左右子树 | 我的提交 |