0x01 一个小故事
《阿里巴巴与四十大盗》中有这样一段小故事:
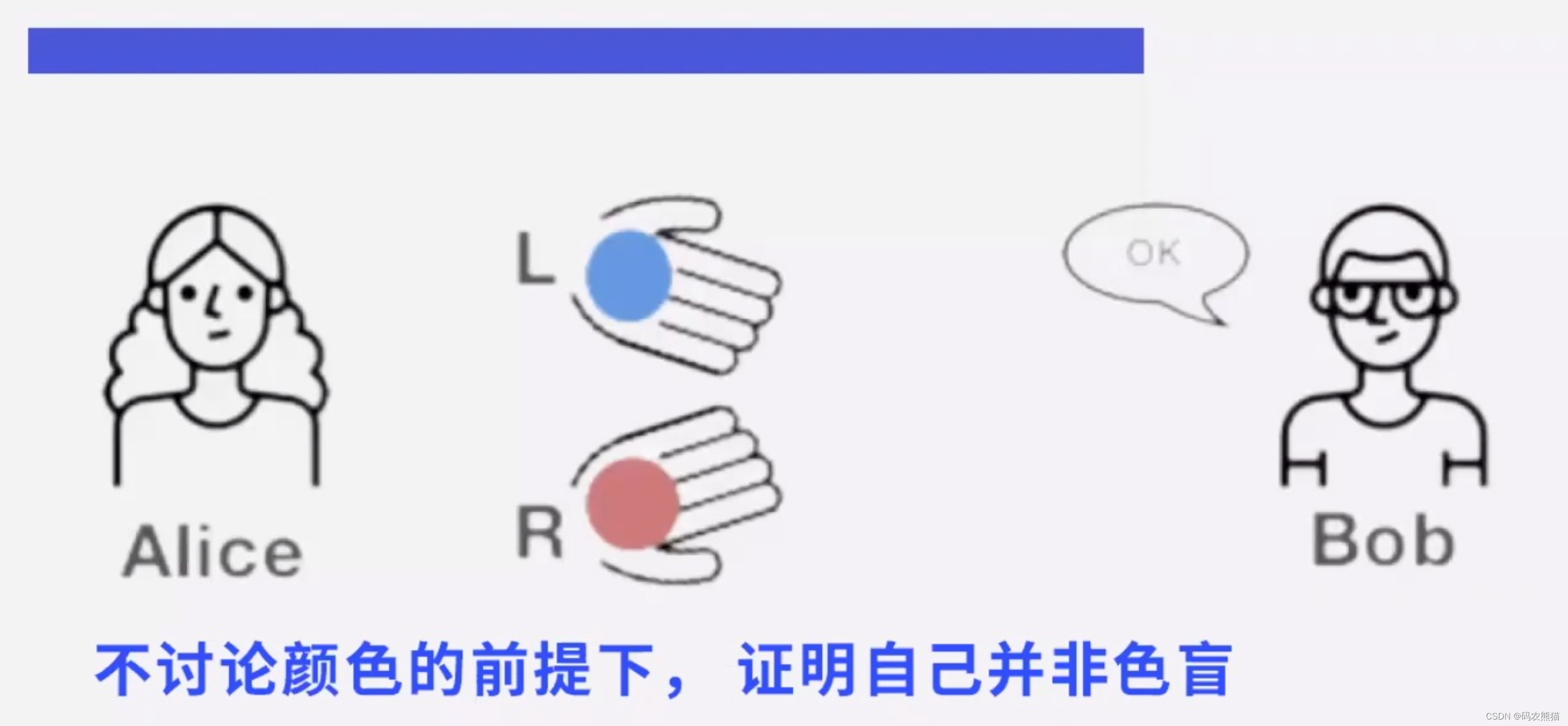
阿里巴巴会芝麻开门的咒语,强盗向他拷问打开山洞石门的咒语,他不想让人听到咒语,又要向强盗证明他知道这个咒语。
那应该怎么办呢?
便对强盗说:「你们离我一箭之地,用弓箭指着我,你们举起右手,我念咒语打开石门,举起左手,我念咒语关上石门,如果我做不到或逃跑,你们就用弓箭射死我。」
这个方案对阿里巴巴没损失,也能让强盗们相信阿里巴巴到底是否知道咒语,于是强盗们同意。强盗举起了右手,只见阿里巴巴的嘴动了几下,石门打开了;强盗举起了左手,阿里巴巴的嘴动了几下,石门又关上了。强盗有点不信,没准这是巧合,但是多试几次过后,他们相信了阿里巴巴。
这样既向强盗们证明了阿里巴巴知道这个咒语的秘密,又没有泄漏这个咒语。
0x02 什么叫做零知识证明
上面的小故事其实就是零知识证明的一个例子。
零知识证明(Zero—Knowledge Proof),简称ZKP。它指的是证明者能够在不向验证者提供任何有用的信息的情况下,使验证者相信某个论断是正确的。
零知识证明实质上是一种涉及两方或更多方的协议,即两方或更多方完成一项任务所需采取的一系列步骤。证明者向验证者证明并使其相信自己知道或拥有某一消息,但证明过程不能向验证者泄漏任何关于被证明消息的信息。
大量事实证明,零知识证明在密码学中非常有用。如果能够将零知识证明用于验证,将可以有效解决许多问题。
0x03 零知识证明的发展历史
现代零知识证明体系最早来源于 Goldwasser、Micali 和 Rackoff 合作发表的论文:《The Knowledge Complexity of Interactive Proof Systems》(即 GMR85),该论文提出于 1985 年,发表于 1989 年。这篇论文主要阐释的是在一个交互系统中,经过 K 轮交互,需要多少知识被交换,从而证明一个证言(statement)是正确的。如果可以让交换的知识为零,则被称之为零知识证明。
早年的零知识证明系统在效率以及可用性方面都有所欠缺,所以一直都停留在理论层面,直到最近 10 年才开始蓬勃发展,伴随着密码学在 crypto 成为显学,零知识证明走向台前,成为至关重要的一个方向。特别是发展出一个通用的、非交互的、证明大小有限的零知识证明协议,是其中最关键的探索方向之一。
基本上零知识证明就是要在证明的速度、验证的速度和证明体积的大小之间做取舍,理想的协议是证明快、验证快、证明体积小。
零知识证明最重要的突破是 Groth 在 2010 年的论文 《Short Pairing-based Non-interactive Zero-Knowledge Arguments》,也是 ZKP 里面最重要的一组 zk-SNARK 的理论先驱。
零知识证明在应用上最重要的进展就是 2015 年 Z-cash 使用的零知识证明系统,实现了对交易及金额隐私的保护,后来发展到 zk-SNARK 和智能合约相结合,zk-SNARK 进入了更为广泛的应用场景。
0x04 零知识证明的性质
根据零知识证明的定义和这些例子,可以得出零知识证明具有以下三个性质:
- 完备性 completeness:如果证明方和验证方都是诚实的,并遵循证明过程的每一步,进行正确的计算,那么这个证明一定是成功的,验证方一定能够接受证明方。
- 合理性 soundness:没有人能够假冒证明方,使这个证明成功。
- 零知识性 zero-knowledge:证明过程执行完之后,验证方只获得了「证明方拥有这个知识」的信息,而没有获得关于这个知识本身的任何信息。
真正的零知识证明运用的是密码学,在不透露数据的情况下证明数据的存在。
0x05 零知识证明算法zkSNARK
Web3里讲的ZKP,通常指其中的zkSNARK(Zero-Knowledge Succinct Non-Interactive Argument of Knowledge-零知识简洁非交互式知识论证)这一类算法。顾名思义,它有以下的特点:
- Zero Knowledge:证明过程零知识,不会暴露多余信息
- Succinct:验证体积小
- Non-interactive:非交互过程
- ARguments:计算具备可靠性,即有限计算能力的证明者不能伪造证明,无限计算能力的证明者可以伪造证明
- of Knowledge:证明者无法在不知道有效信息的情况下构建出一个参数和证明
- 对于证明者来说,在不知道证据(Witness,比如一个哈希函数的输入或者一个确定 Merkle-tree 节点的路径)的情况下,构造出一组参数和证明是不可能的。
0x06 zkSNARK的核心实现
zkSNARK 的整体技术实现过程相当繁琐,这里主要讲下其核心思想。
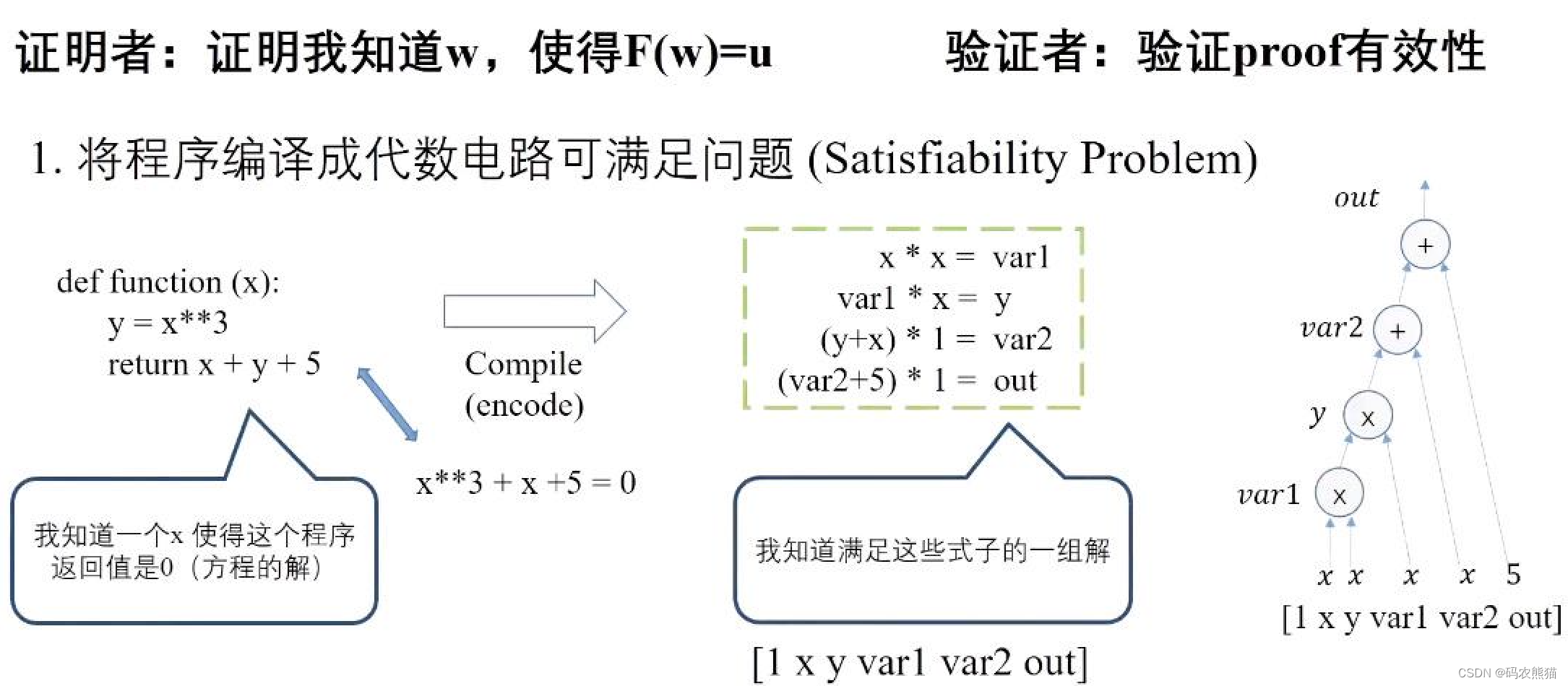
我们从一个方程式开始,X^3 + X + 5 = 35,显然解是 3。那么现在,证明者如何向验证者证明自己知道方程的解是 3,而又不告诉验证者这个解呢?
首先,我们将方程转化为计算机语言,这很容易实现:
y = x*3
return x + y + 5
接着,我们将上面的代码拍平。所谓将代码拍平,是指让代码一次只做一件事。
拍平后,代码变成以下语句:
var1 = x * x
y = var1 * x
var2 = y + x
~out = var2 + 5
然后,我们引入 R1CS 一阶约束系统(rank-1 constraint system),R1CS 是一个由三向量组(a, b, c)组成的序列,同时有一个解向量 v,v 满足 v·a * v·b - v·c = 0。
在本例中,s 的结构为(~one, x, ~out, var1, y, var2),可见其由一个特殊的 ~one、方程的解 x、方程的输出 ~out 和一系列中间变量(拍平后的语句等号左边的变量)构成,其顺序不重要,只要保证有序即可。
我们把语句变换成如下形式,来方便我们求解 abc:
x * x - var1 = 0
var1 * x - y = 0
y + x - var2 = 0
var2 + 5 - ~out = 0
我们很容易得出第一个式子对应的三个向量:
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]
推导过程其实很简单,我们知道要满足 v·a * v·b - v·c = 0,那么对应第一个式子 x * x - var1 = 0,只需要 v·a = x、v·b = x、v·c = var1 即可,而 s =(~one, x, ~out, var1, y, var2),那么 a 只要在 x 的位置等于 1,其余位置等于 0,即得出(0,1,0,0,0,0)。
我们对每个式子验证 v·a * v·b - v·c = 0,其本质是在验证每一步都得到了正确的计算,也即如果我们可以验证每一步都是正确的,那么最终结果也一定是正确的。
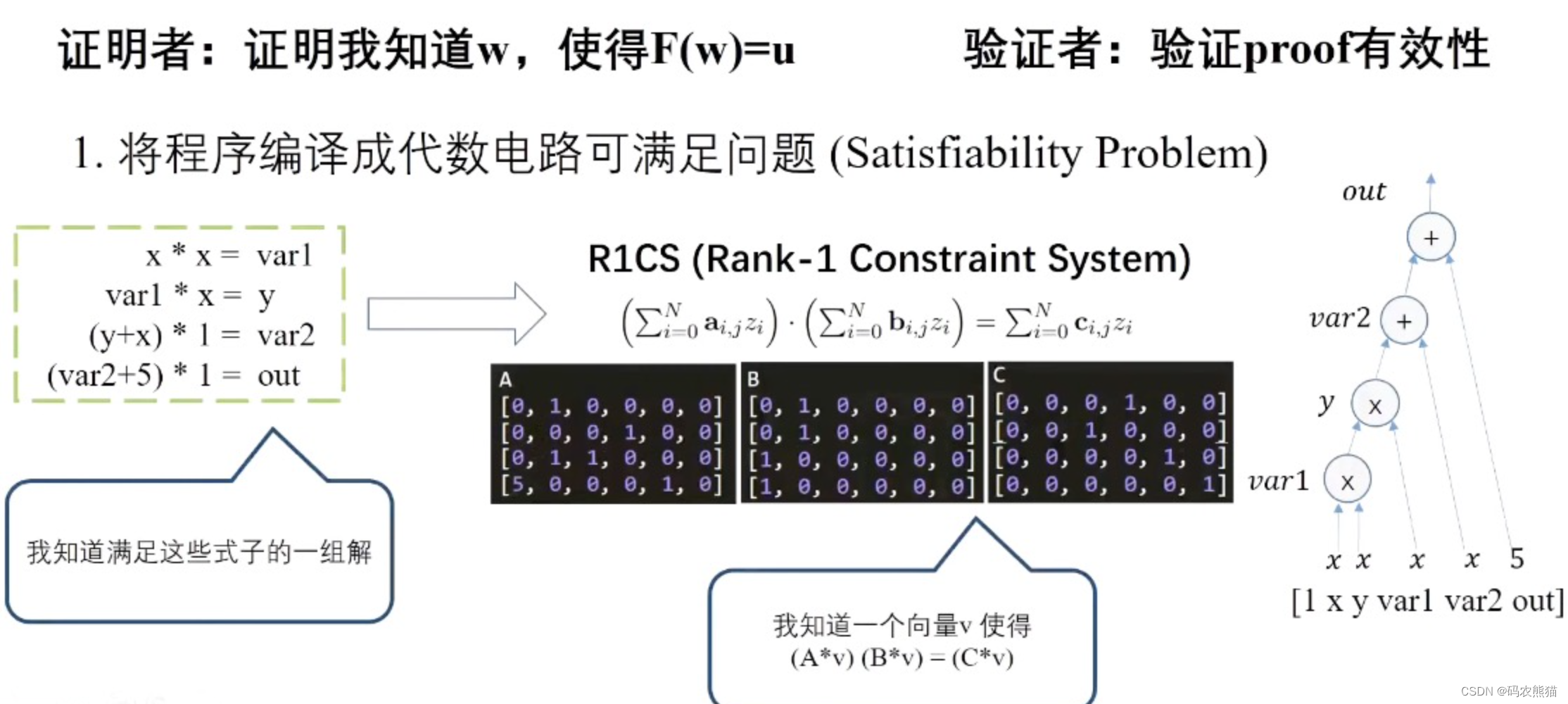
以上的每一步,看似都在舍近求远,因为 v 里本身就包含了方程的解 x,验证者只需把 x 代入就能进行验证。但从另一个角度看,通过这一系列的转换,我们构建了一种将证明和验证分离的方式。在证明过程中,证明者需要知道解并生成一系列中间结果,而验证者则只需要验证其一系列结果构成的解向量是否满足一系列约束,而不需要关心这个解到底是多少。
现在只剩一个问题留待解决,就是能否通过一种方式,让验证者看不到裸着的解 x,同时依然可以进行验证过程。答案是肯定的,借由椭圆曲线、双线性对数运算和指数知识假设这一系列数学手段我们就可以做到这一点。
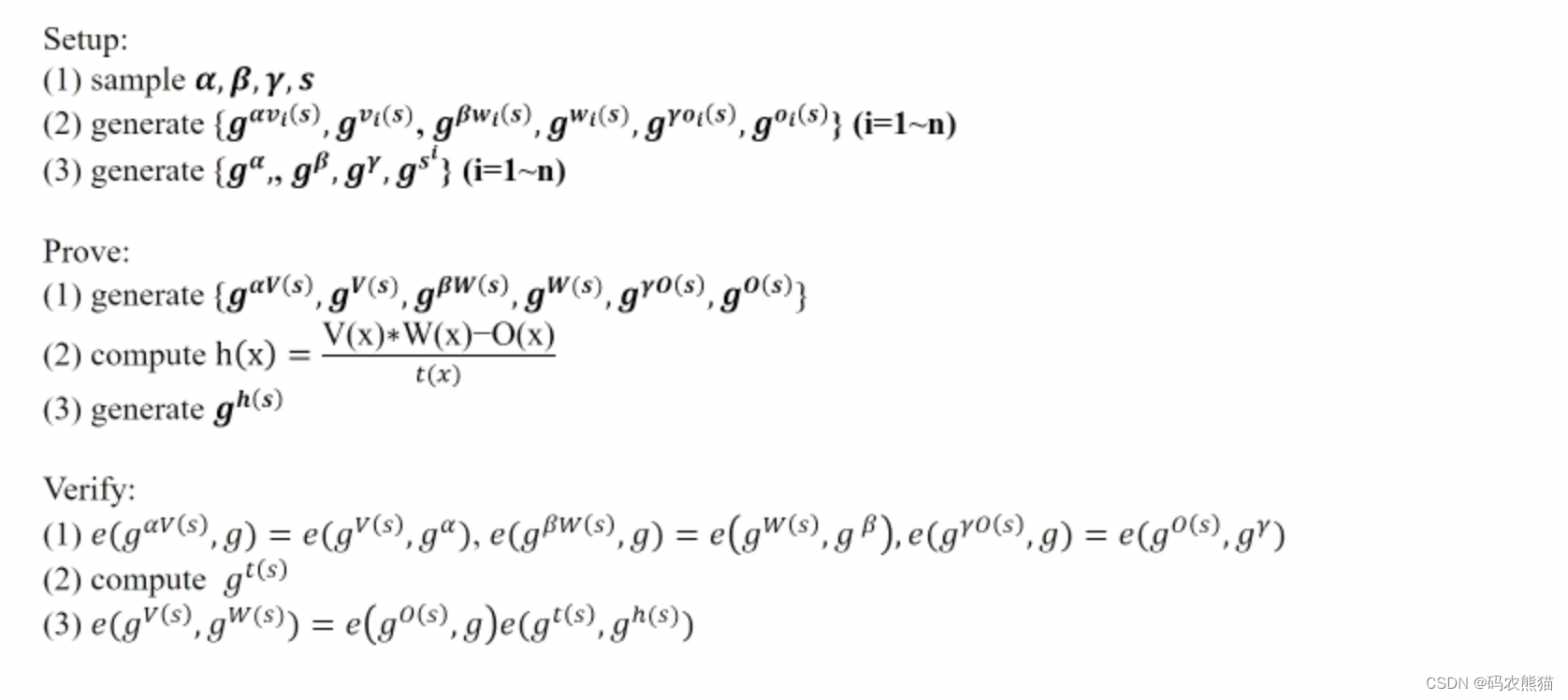
0x07 零知识证明的未来
Alex Pruden说:“改变 Web3 的技术之一,无疑是零知识 (ZK) 密码学。作为区块链应用生态在隐私、安全性和完整性等方面的游戏规则改变者,ZKP(零知识证明)的加速投资和发展是它正在为黄金时期做好准备的重要信号。”
未来将是一个注重隐私保护的网络时代,零知识证明被视为Web3的重要变革因素,随着技术的创新和应用的拓展,零知识证明技术正在迎来它的黄金时代。
更多技术干货,请关注公众号【码农熊猫】