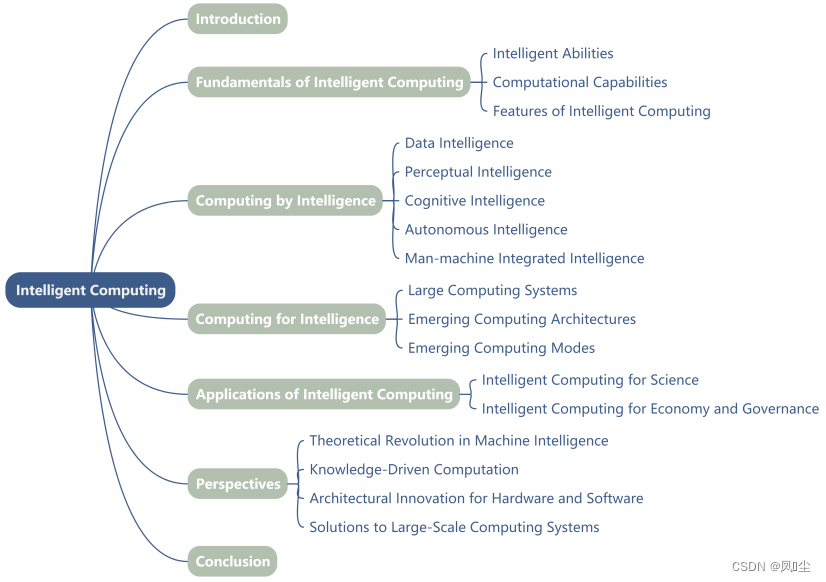
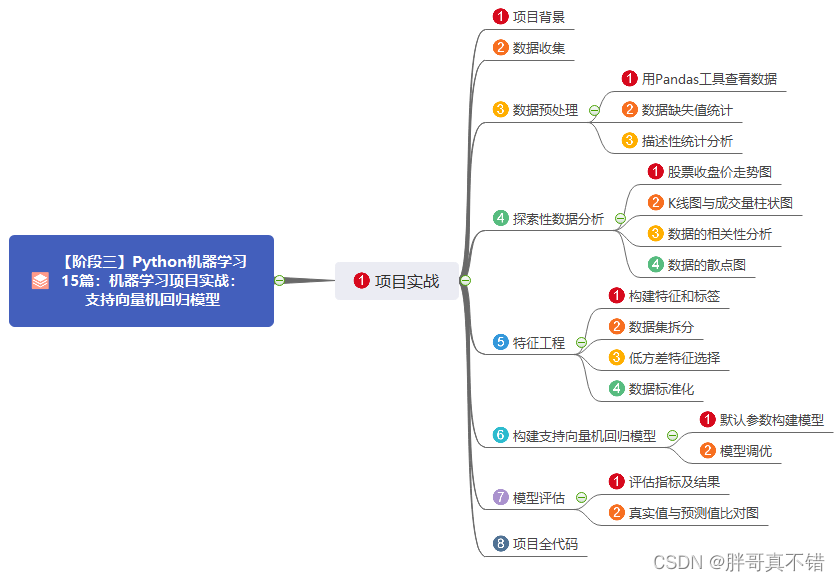
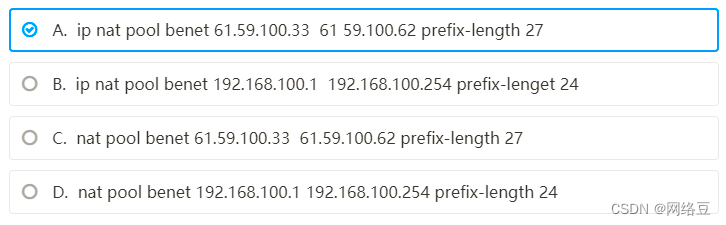
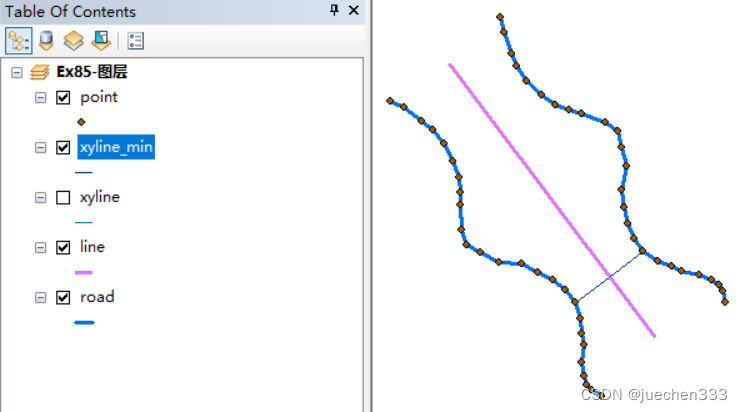
题目：

请你设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。实现LRUCache类：

LRUCache(int capacity) 以正整数作为容量capacity初始化 LRU 缓存
int get(int key) 如果关键字key存在于缓存中，则返回关键字的值，否则返回-1 。
void put(int key, int value) 如果关键字key已经存在，则变更其数据值value；如果不存在，则向缓存中插入该组key-value。如果插入操作导致关键字数量超过capacity，则应该逐出最久未使用的关键字。
函数get和put必须以O(1)的平均时间复杂度运行。

示例

输入[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”][[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出[null, null, null, 1, null, -1, null, -1, 3, 4]
解释LRUCache lRUCache = new LRUCache(2);lRUCache.put(1, 1); // 缓存是 {1=1}lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}lRUCache.get(1); // 返回 1lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}lRUCache.get(2); // 返回 -1 (未找到)lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}lRUCache.get(1); // 返回 -1 (未找到)lRUCache.get(3); // 返回 3lRUCache.get(4); // 返回 4

标题题解

该题目的核心主要是get与put函数。get函数的要求非常简单就是通过key获取相应的value，hash表即可满足题目要求。put函数主要超过capacity的时候需要把最久未使用的关键字删除，再添加新的key-value。这里显然需要对key进行排序，自然想到的就是Python3中collections中的OrderedDict。代码如下：

class LRUCache:

    def __init__(self, capacity: int):
        #定义一个dict
        self.capacity=capacity
        #定义一个有序字典
        self.LRU_dic=collections.OrderedDict()
        #使用一个变量记录dic的数据量
        self.used_num=0

    def get(self, key: int) -> int:
        if key in self.LRU_dic:
            #如果被使用了利用move_to_end移动到队尾，保证了LRU_dic是按使用顺序排序的
            self.LRU_dic.move_to_end(key)
            return self.LRU_dic.get(key)
        else:
            return -1

    def put(self, key: int, value: int) -> None:
        if key in self.LRU_dic:         
            self.LRU_dic[key]=value
            self.LRU_dic.move_to_end(key)
        else:
            #判断当前已有数量是否超过capacity
            if self.used_num==self.capacity:
                #删除首个key，因为首个key是最久未使用的
                self.LRU_dic.popitem(last=False)
                self.used_num-=1
            self.LRU_dic[key]=value
            self.used_num+=1

然后，直接调用包通常不是面试的时候考察的主要能力。因此需要根据一些数据结构来实现OrderedDict类似的功能。
可以发现哈希表肯定是需要的，能存储key,value相关信息。这里一个主要的需求是一个序的数据结构能在头部与尾部都实现O(1)时间复杂度的操作。list也能满足这个要求，但是list对于元素的查询、更新以及有排序操作的支持不是很友好。显然这里使用双向链表比较合适。下面详细介绍一下哈希表与双向链表。数据结构清楚了实现就比较容易了。
先介绍下双向链表。

pre表示前向指针，key,value就是键值，next表示下一步指针指的节点。初始化只有head与tail两个节点，这里把新使用的节点放到链表尾部，头部链表节点就是最久未使用的节点。

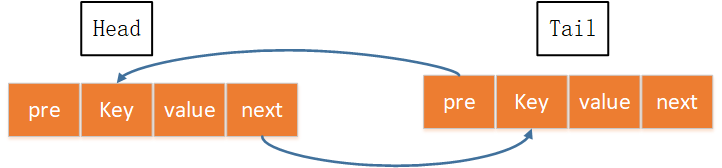
因为使用过的key需要把相应的链表节点移动到队尾，因此需要实现类似OrderedDict的move_to_end这个函数的功能。如果超出capacity的时候要删除最久未使用的节点也就是删除head.next节点，也需要实现一个表头节点删除的功能。定义完链表，hash表就好实现了key，对应给定的key，value对应的是双向链表中的节点。这样通过key就能在O(1)时间定位到双向链表中的节点。代码实现如下：

class LRUCache:
    class D_link:
        def __init__(self,key=0,value=0):
            self.key=key
            self.value=value
            self.pre=None
            self.next=None


    def __init__(self, capacity: int):
        #定义一个dict
        self.capacity=capacity
        self.LRU_dic={}
        #使用一个变量记录dic的数据量
        self.used_num=0
        #初始化双向链表
        self.head=LRUCache.D_link()
        self.tail=LRUCache.D_link()
        self.head.next=self.tail
        self.tail.pre=self.head

    def get(self, key: int) -> int:
        if key in self.LRU_dic:
            node=self.LRU_dic.get(key)
            #因为访问过需要移动到链表尾
            self.move_to_end(node)
            return node.value
        else:
            return -1

    def put(self, key: int, value: int) -> None:
        if key in self.LRU_dic:
            #更新LRU_dic的value         
            node= self.LRU_dic[key]
            node.value=value
            self.move_to_end(node)
        else:
            #判断当前已有数量是否超过capacity
            if self.used_num==self.capacity:
                #删除双链表最前面的Node
                del_key=self.del_head()
                self.used_num-=1
                #从LRU_dic中删除Key
                del self.LRU_dic[del_key]
            new_node=LRUCache.D_link(key,value)
            #在链表尾部插入
            self.insert_node(new_node)
            self.LRU_dic[key]=new_node
            self.used_num+=1
    
    def move_to_end(self,node):
        #首先把node取出来
        pre_node=node.pre
        post_node=node.next
        pre_node.next=post_node
        post_node.pre=pre_node
        tail_pre=self.tail.pre
        tail_pre.next=node
        node.pre=tail_pre
        node.next=self.tail
        self.tail.pre=node

    def del_head(self):
        key=self.head.next.key
        post_node=self.head.next.next
        self.head.next=post_node
        post_node.pre=self.head
        return key

    def insert_node(self,node):
        pre_tail=self.tail.pre
        pre_tail.next=node
        node.pre=pre_tail
        node.next=self.tail
        self.tail.pre=node