文章目录
- 基本概念
- 模拟栈
- 数据结构-栈:stack
- 头文件
- 定义
- 基本操作
- 实例:火车进栈
- 题目大意
- 解题思路
- AC代码
基本概念
栈的定义
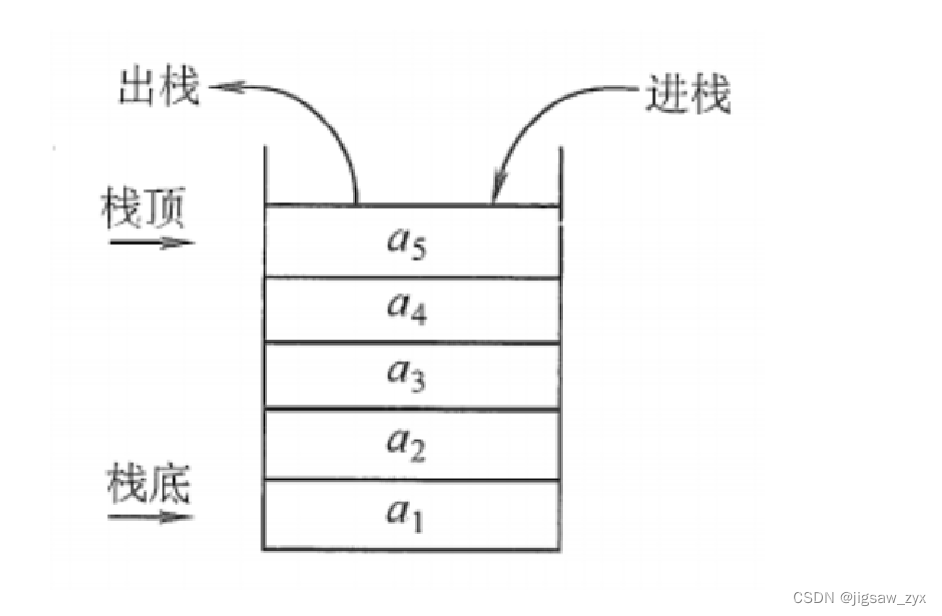
栈(stack)是限定仅在表尾进行插入或者删除的线性表。对于栈来说,表尾端称为栈顶(top),表头端称为栈低(bottom)。不含元素的空表称为空栈。因为栈限定在表尾进行插入或者删除,所以栈又被称为后进先出的线性表(简称LIFO:Last in, First out.结构)。
例如:stack:1 2 3 4 5
类似于放盘子
视图如下:
后进先出
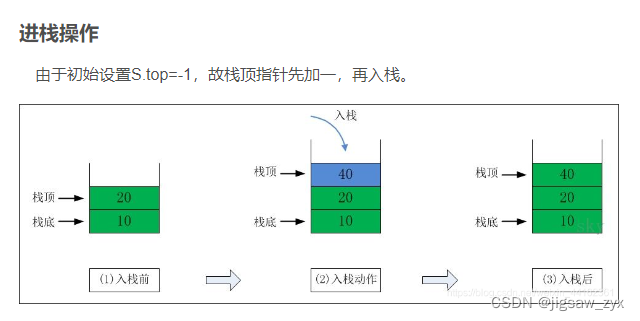
模拟栈
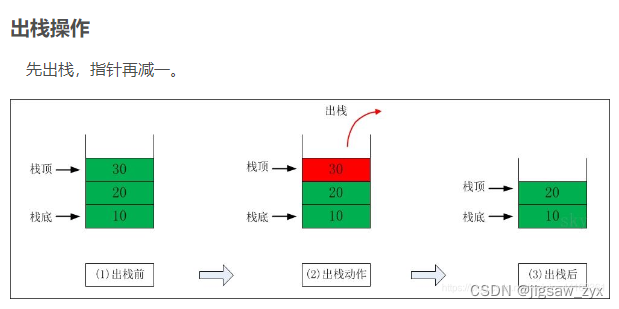
先进后出
比较简单直接放截屏
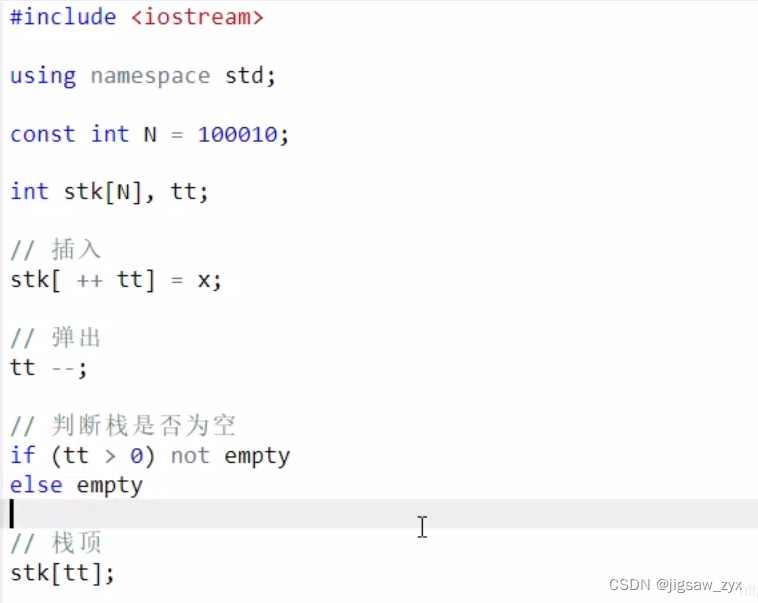
#include<bits/stdc++.h>
using namespace std;
# 用数组模拟栈
const int N=100;
int stk[N],tt=0; # stk代表的是栈数组,tt就是栈顶指针
# 栈顶
栈顶指针:tt
栈顶元素:stk[tt];
# 入栈:栈顶指针先+1,然后入栈
stk[++tt]=66;
# 出栈:栈顶指针先-1,然后出栈
tt--;
# 判断栈是否为空
if(tt==0) true
else false
数据结构-栈:stack
栈,先进后出
头文件
#include <stack>
定义
stack<int> st;
基本操作
empty() 堆栈为空则返回真
pop() 移除栈顶元素
push() 在栈顶增加元素
size() 返回栈中元素数目
top() 返回栈顶元素
#include<bits/stdc++.h>
#include<stack>
// 包含了stack这个头文件
using namespace std;
// 使用数据结构的栈
//定义一个栈
stack<int> stk;
/*
empty() 堆栈为空则返回真
pop() 移除栈顶元素
push() 在栈顶增加元素
size() 返回栈中元素数目
top() 返回栈顶元素
*/
int main(){
//入栈
stk.push(10);
stk.push(20);
stk.push(30);
//查看栈顶元素
cout<<stk.top();
//cout == print
//出栈
stk.pop();
//查看栈顶元素
cout<<" "<<stk.top();
//查看栈元素个数
cout<<" size="<<stk.size();
return 0;
}
实例:火车进栈
原题链接:
https://www.acwing.com/problem/content/131/
题目描述
这里有 n 列火车将要进站再出站,但是,每列火车只有 1 节,那就是车头。
这 n 列火车按 1 到 n 的顺序从东方左转进站,这个车站是南北方向的,它虽然无限长,只可惜是一个死胡同,而且站台只有一条股道,火车只能倒着从西方出去,而且每列火车必须进站,先进后出。
也就是说这个火车站其实就相当于一个栈,每次可以让右侧头火车进栈,或者让栈顶火车出站。
车站示意如图:
出站<—— <——进站
|车|
|站|
|__|
现在请你按《字典序》输出前 20 种可能的出栈方案。
输入格式
输入一个整数 n,代表火车数量。
输出格式
按照《字典序》输出前 20 种答案,每行一种,不要空格。
数据范围
1≤n≤20
输入样例:
3
输出样例:
123
132
213
231
321
题目大意
输出 1 、 2 、 . . . . . . 、 n {1、2、......、n} 1、2、......、n的按字典序前20个出栈情况
解题思路
模拟栈的出栈情况,对于每一次栈有两个选择,要么进栈,要么出栈。
由此,我们可以知道我们需要三个变量:可以用stack3来表示入栈的数值,每入一次栈就加一;用stack2表示栈中的情况,当栈不为空的时候才可以出栈;stack1来表示出栈情况
我们可以通过递归来实现整个过程:
1.当stack1的长度为n时,那么达到边界
2.当stack2不为空的时候出栈
3.入栈
注意:每次操作后记得还原栈的情况

AC代码
#include<iostream>
#include<vector>
#include<stack>
using namespace std;
int n;
int cnt = 20,stack3;
vector<int> stack1;
stack<int> stack2;
void dfs(){
if(!cnt) return ;
//边界条件
if(stack1.size()==n){
cnt--;
for(int i=0;i<n;i++) cout<<stack1[i];
cout<<endl;
return ;
}
//出栈
if(!stack2.empty()){
stack1.push_back(stack2.top());
stack2.pop();
dfs();
stack2.push(stack1.back());
stack1.pop_back();
}
//入栈
if(stack3<n){
stack3++;
stack2.push(stack3);
dfs();
stack2.pop();
stack3--;
}
return;
}
int main(){
cin>>n;
dfs();
return 0;
}