💕"2024.3.28小米汽车发布"💕
作者:Lvzi
文章主要内容:算法系列–动态规划–背包问题(2)–01背包拓展题目
大家好,今天为大家带来的是
算法系列--动态规划--背包问题(2)--01背包拓展题目
1.分割等和⼦集
链接:
https://leetcode.cn/problems/partition-equal-subset-sum/

分析:
本题属于01背包问题
从数组中选择一些数据,使其刚好符合某种带限制条件的和,就符合01背包问题的思路
01背包问题就是选择一些物品,实现不超过背包最大容量的最大价值
本题是选择一些数,判断能够实现最大和刚好等于sum/2的情况
还有一个是在分析状态转移方程时,最后一个位置选或者不选也可以用01问题
代码:
class Solution {
public boolean canPartition(int[] nums) {
int n = nums.length;
int sum = 0;
for(int x : nums) sum += x;// 求和
if(sum % 2 == 1) return false;// 特判
int N = sum / 2;
// 创建dp表
boolean[][] dp = new boolean[n + 1][N + 1];
dp[0][0] = true;// 初始化
for(int i = 1; i <= nums.length; i++) {
for(int j = 1; j <= sum / 2; j++) {
dp[i][j] = (dp[i - 1][j])
|| (j - nums[i - 1] >= 0 && dp[i - 1][j - nums[i - 1]]);
}
}
// 返回值
return dp[nums.length][sum / 2];
}
}
空间优化后的代码:
class Solution {
public boolean canPartition(int[] nums) {
int n = nums.length, sum = 0;
for(int x : nums) sum += x;
if(sum % 2 == 1) return false;
int N = sum / 2;
boolean[] dp = new boolean[N + 1];
dp[0] = true;
for(int i = 1; i <= n; i++)
for(int j = sum / 2; j >= nums[i - 1]; j--)
dp[j] = dp[j] || dp[j - nums[i - 1]];
return dp[sum / 2];
}
}
2.⽬标和
链接:
https://leetcode.cn/problems/target-sum/

分析:
题目要求是必须用到数组里面的所有数字进行拼接(可正可负),判断可以拼接为target的最大组合数
首先,因为要用到数组中所有的数字,所以可以先把数组总和sum求出,接着我们可以把sum拆分为两部分,一部分是拼接+的数字总和a,另一部分是拼接-的总和b(b是大于0的,这里仅仅只是数字的相加),则可以得出:
a + b == suma - b == target
将两式相加可得:
a == (sum + target) / 2
示意图:
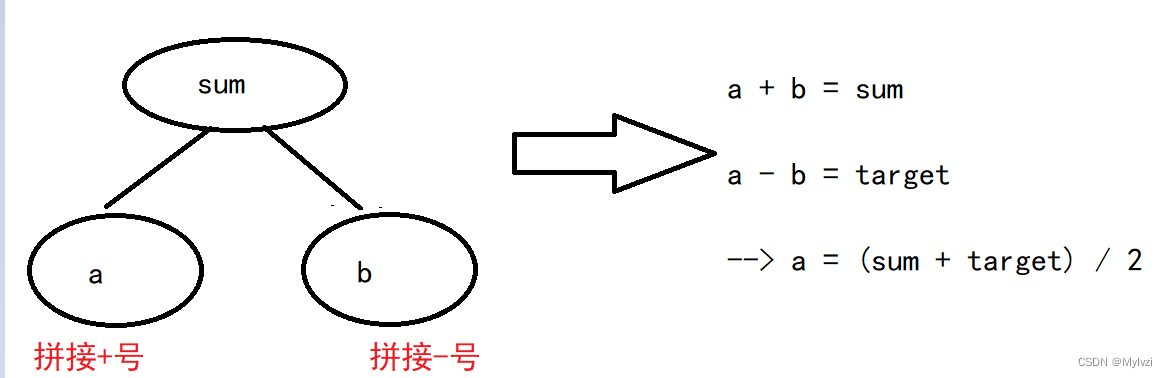
那么本道题就可以转化为在数组中挑选若干个数,使其和等于a的最大组合数,这不就是01背包问题吗!,在一个集合内部挑选若干个物品,在满足某个限制的前提下,实现xxxx
说明:求出a之后还需要判断是否越界,主要有两种不符合条件的情况:
a < 0,因为本题的target可以是负数,所以a可能是负数,但是数组中的数全是大于0的,根部无法凑出一个小于0的数(sum + target) / 2 != 0:当除不尽的时候就代表不存在这样的a,也就无法凑出target,返回0
接下来就是动态规划的思路:
- 状态表示:
dp[i][j] :nums在[1,i]区间数字,和为j的最大组合数
- 状态转移方程
- 和经典的背包问题一样,也是根据最后一个位置
选或不选来推导状态转移方程,要注意的是,本题求的是最大组合数,也就是dp[i][j]应该是两种情况的总和

- 和经典的背包问题一样,也是根据最后一个位置
- 初始化
- 初始化主要考虑第一行和第一列

- 填表顺序
- 从左往右,从上往下
- 返回值
- dp[n][a]
代码:
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int a = 0, sum = 0;
for(int n : nums) sum += n;// 求和
a = (target + sum) / 2;// 计算目标值
if(a < 0 || (sum + target) % 2 == 1) return 0;
// 创建dp表
int n = nums.length;
int[][] dp = new int[n + 1][a + 1];
dp[0][0] = 1;
// 填表
for(int i = 1; i <= n; i++) {
for(int j = 0; j <= a; j++) {
dp[i][j] = dp[i - 1][j];
if(j - nums[i - 1] >= 0)
dp[i][j] += dp[i - 1][j - nums[i - 1]];
}
}
return dp[n][a];
}
}
空间优化后的代码
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int a = 0, sum = 0;
for(int n : nums) sum += n;// 求和
a = (target + sum) / 2;// 计算目标值
if(a < 0 || (sum + target) % 2 == 1) return 0;
// 创建dp表
int n = nums.length;
int[] dp = new int[a + 1];
dp[0] = 1;
// 填表
for(int i = 1; i <= n; i++)
for(int j = a; j >= nums[i - 1]; j--)// 注意优化后的便利顺序
dp[j] += dp[j - nums[i - 1]];
return dp[a];
}
}
第一行不初始化,放到填表之中,也是背包问题常用的一种优化手段
3.最后⼀块⽯头的重量II
链接:
https://leetcode.cn/problems/last-stone-weight-ii/description/

分析:
本题的难点就在于转化,光看数字无法得出什么有效的结论,我们将数字换为字母,看能得出什么结论:

最后发现整个问题的思路很像目标和那道题目(就在上面),但是目标和那道题目最终求的是一个具体数字,本题要求的是最后的值的绝对值尽可能的小,还是套用和目标和一样的分析思路,整个数组的和是sum,可以根据匹配的符号不同分为两部分a,b
假设a>b,则求得就是a-b的最小值,对于数组中的每一个数都是选或不选,这就是01背包问题的特征,可以使用01背包问题的思路解决
状态表示:
dp[i][j]:在[1,i]区间内,选取一定的数字,在不超过j的前提下,可以实现的最大和
状态转移方程和初始化都比较简单,这里不再赘述
返回值:
- 最终返回的应该是a-b的最小值
a = dp[n][sum/2],那么b = sum - a,所以最终应该返回sum - 2 * dp[n][sum/2]

class Solution {
public int lastStoneWeightII(int[] stones) {
int n = stones.length, sum = 0;
for(int x : stones) sum += x;
int[][] dp = new int[n + 1][sum/2 + 1];// 创建dp表
// 填表
for(int i = 1; i <= n; i++) {
for(int j = 0; j <= sum/2; j++) {
dp[i][j] = dp[i - 1][j];
if(j - stones[i - 1] >= 0)
dp[i][j] = Math.max(dp[i][j],dp[i - 1][j - stones[i - 1]] + stones[i - 1]);
}
}
return sum - 2 * dp[n][sum/2];// 返回(a-b)绝对值的最小值
}
}
空间优化后的代码:
class Solution {
public int lastStoneWeightII(int[] stones) {
int n = stones.length, sum = 0;
for(int x : stones) sum += x;
int[] dp = new int[sum/2 + 1];// 创建dp表
// 填表
for(int i = 1; i <= n; i++)
for(int j = sum/2; j >= stones[i-1]; j--)
dp[j] = Math.max(dp[j],dp[j - stones[i - 1]] + stones[i - 1]);
return sum - 2 * dp[sum/2];// 返回(a-b)绝对值的最小值
}
}
以上就是
算法系列--动态规划--背包问题(2)--01背包拓展题目全部内容,下一篇文章将会带来完全背包问题的介绍,敬请期待,我是LvZi