题目描述

LQ 国拥有 $n$ 个城市，从 $0$ 到 $n-1$ 编号，这 $n$ 个城市两两之间都有且仅有一条双向道路连接，这意味着任意两个城市之间都是可达的。每条道路都有一个属性 $D$，表示这条道路的灰尘度。当从一个城市 A 前往另一个城市 B 时，可能存在多条路线，每条路线的灰尘度定义为这条路线所经过的所有道路的灰尘度之和，LQ 国的人都很讨厌灰尘，所以他们总会优先选择灰尘度最小的路线。

LQ 国很看重居民的出行环境，他们用一个指标 $P$ 来衡量 LQ 国的出行环境，$P$ 定义为：

$$P=\sum _{i=0}^{n-1}\sum _{j=0}^{n-1}d(i,j)$$

其中 $d(i,j)$ 表示城市 $i$ 到城市 $j$ 之间灰尘度最小的路线对应的灰尘度的值。

为了改善出行环境，每个城市都要有所作为，当某个城市进行道路改善时，会将与这个城市直接相连的所有道路的灰尘度都减少 $1$，但每条道路都有一个灰尘度的下限值 $L$，当灰尘度达到道路的下限值时，无论再怎么改善，道路的灰尘度也不会再减小了。

具体的计划是这样的：

• 第 $1$ 天，$0$ 号城市对与其直接相连的道路环境进行改善；
• 第 $2$ 天，$1$ 号城市对与其直接相连的道路环境进行改善；

……

• 第 $n$ 天，$n-1$ 号城市对与其直接相连的道路环境进行改善；
• 第 $n+1$ 天，$0$ 号城市对与其直接相连的道路环境进行改善；
• 第 $n+2$ 天，$1$ 号城市对与其直接相连的道路环境进行改善；

……

LQ 国想要使得 $P$ 指标满足 $P\le Q$。请问最少要经过多少天之后，$P$ 指标可以满足 $P\le Q$。如果在初始时就已经满足条件，则输出 $0$；如果永远不可能满足，则输出 $-1$。

输入格式

输入的第一行包含两个整数 $n,Q$，用一个空格分隔，分别表示城市个数和期望达到的 $P$ 指标。

接下来 $n$ 行，每行包含 $n$ 个整数，相邻两个整数之间用一个空格分隔，其中第 $i$ 行第 $j$ 列的值 $D_{i,j}(D_{i,j}=D_{j,i},D_{i,i}=0)$ 表示城市 $i$ 与城市 $j$ 之间直接相连的那条道路的灰尘度。

接下来 $n$ 行，每行包含 $n$ 个整数，相邻两个整数之间用一个空格分隔，其中第 $i$ 行第 $j$ 列的值 $L_{i,j}(L_{i,j}=L_{j,i},L_{i,i}=0)$ 表示城市 $i$ 与城市 $j$ 之间直接相连的那条道路的灰尘度的下限值。

输出格式

输出一行包含一个整数表示答案。

样例 #1

样例输入 #1

3 10
0 2 4
2 0 1
4 1 0
0 2 2
2 0 0
2 0 0

样例输出 #1

2

提示

【样例说明】

初始时的图如下所示，每条边上的数字表示这条道路的灰尘度：

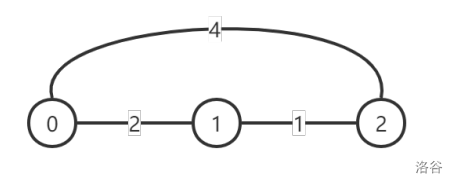
此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

• $d(0,0)=0,d(0,1)=2,d(0,2)=3$；
• $d(1,0)=2,d(1,1)=0,d(1,2)=1$；
• $d(2,0)=3,d(2,1)=1,d(2,2)=0$。

初始时的 $P$ 指标为 $(2+3+1)\times 2=12$，不满足 $P\le Q=10$;

第一天，$0$ 号城市进行道路改善，改善后的图示如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EVkfYzSE-1673431827042)(https://cdn.luogu.com.cn/upload/image_hosting/mrhf5wx6.png)]

注意到边 $(0,2)$ 的值减小了 $1$，但 $(0,1)$ 并没有减小，因为 $L_{0,1}=2$ ，所以 $(0,1)$ 的值不可以再减小了。此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

• $d(0,0)=0,d(0,1)=2,d(0,2)=3$，
• $d(1,0)=2,d(1,1)=0,d(1,2)=1$，
• $d(2,0)=3,d(2,1)=1,d(2,2)=0$。

此时 $P$ 仍为 $12$。

第二天，1 号城市进行道路改善，改善后的图示如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KFsHlrHB-1673431827042)(https://cdn.luogu.com.cn/upload/image_hosting/tjxis3yb.png)]

此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

• $d(0,0)=0,d(0,1)=2,d(0,2)=2$，
• $d(1,0)=2,d(1,1)=0,d(1,2)=0$，
• $d(2,0)=2,d(2,1)=0,d(2,2)=0$。

此时的 $P$ 指标为 $(2+2)\times 2=8<Q$，此时已经满足条件。

所以答案是 $2$。

【评测用例规模与约定】

• 对于 $30\%$ 的评测用例，$1\le n\le 10$，$0\le L_{i,j}\le D_{i,j}\le 10$；
• 对于 $60\%$ 的评测用例，$1\le n\le 50$，$0\le L_{i,j}\le D_{i,j}\le 10^5$；
• 对于所有评测用例，$1\le n\le 100$，$0\le L_{i,j}\le D_{i,j}\le 10^5$，$0\le Q\le 2^{31}-1$。

蓝桥杯 2022 国赛 A 组 F 题。

解题思路：

emm这题虽然描述有点长，但实际思路并不难想

因为对于$P$的定义已经给出很明显的提示了——多源最短路径，用Floyd

然后就是本题的图的特殊之处：灰尘度的变化

这个特殊之处直接导致了想一次Floyd直接解决问题是不可能的

因为Floyd得到的最短路径抽象去了路径上的点，那样就不知道哪条最短路径会缩短了

所以要想其他办法

去思考本题的答案会发现：

1）天数越多，就越可能达标

2）本题要求的是最少需要多少天

这不就是二分法嘛

然后就明白了大概的解题思路：二分搜索天数，用Floyd判断这天的灰尘度是否达标

接下来就是一些细节的问题了，例如

对于完全图用二维数组存图、每轮搜索之前都需要根据天数初始化图的边权

计算得到天数的范围是$0$~$10^7$

以及最重要的，关于数据范围的问题

$q$的最大值已经超出了int所能达到的精度，应该用long long存储

即使是long long，累加结束之后也可能溢出（$边权和max=1^{5^3}$），故需要加上正数判断

说了这么多，最后，AC代码如下

//Floyd
#include <iostream>
using namespace std;
const int max_n = 100;
const int max_l = 1e5;
const int max_d = 1e5;
const long long max_q = 0xFFFFFFFF - 1;
const int NaN = 0x3F3F3F3F;

int map[max_n][max_n] = { 0 };//存图
int limit[max_n][max_n] = { 0 };//最小灰尘度
int ans = -1;
int n;
long long q;
int dist[max_n][max_n] = { 0 };//临时图

bool floyd(int day) {
	for (int i = 0; i < n; i++) {//初始化
		for (int j = 0; j < n; j++) {
			dist[i][j] = max(map[i][j] - day / n - (day % n >= i + 1 ? 1 : 0), limit[i][j]);
		}
	}

	for (int i = 0; i < n; i++) {//Floyd
		for (int j = 0; j < n; j++) {
			for (int z = 0; z < n; z++) {
				dist[j][z] = min(dist[j][z], dist[j][i] + dist[i][z]);
			}
		}
	}

	long long sum = 0;
	for (int i = 0; i < n; i++) {//累加
		for (int j = 0; j < n; j++) {
			sum += dist[i][j];
		}
	}
	if (sum >= 0 && sum <= q) {//溢出判断 && 达标
		ans = day;
		return true;
	}
	else return false;
}

void bin_search() {//二分
	int left = -1, right = max_n * max_l + 1;
	while (left + 1 != right) {
		int middle = (left + right) / 2;
		if (floyd(middle)) {
			right = middle;
		}
		else {
			left = middle;
		}
	}
}

int main() {
	cin >> n >> q;
	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			cin >> map[i][j];
	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			cin >> limit[i][j];

	bin_search();
	cout << ans;
	return 0;
}