SVM(Support Vector Machine)

Vapnik发明用于解决二分类问题的机器学习算法。

线性可分与非线性可分

在二维平面中，线性可分指的是可以通过一条直线对平面上的点进行划分使得标签相同的点在直线的同一侧，标签不同的点在直线的不同侧。

在二维平面中，非线性可分则是指除去线性可分的情况。

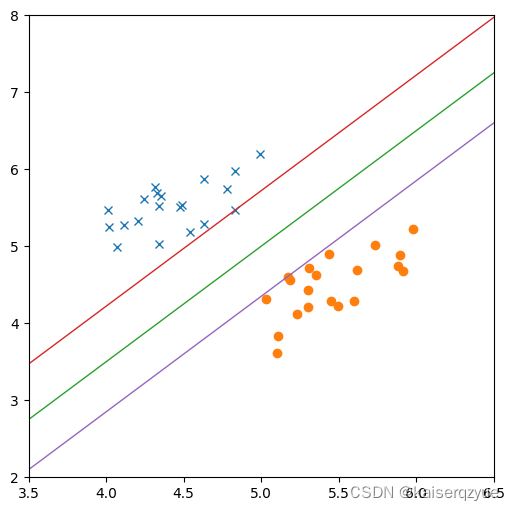
下面是一个线性可分的例子：

import matplotlib.pyplot as plot
from random import random
x1 = []
x2 = []
y1 = []
y2 = []
figSize = (6, 6)
dotNum = 20
for i in range(dotNum):
    x1.append(random() * 1 + 4.5 - 0.5)
    x2.append(random() * 1 + 4.5 + 0.5)
    y1.append(x1[-1] + random() * 1 + 0.5)
    y2.append(x2[-1] - random() * 1 - 0.5)

fig, ax = plot.subplots(figsize = figSize)
ax.axis([3.5, 6.5, 2, 8])
ax.plot(x1, y1, "x")
ax.plot(x2, y2, "o")
ax.plot([3, 7], [3, 7], linewidth = 1)
ax.plot([3, 7], [2, 8], linewidth = 1)
ax.plot([3, 7], [1, 9], linewidth = 1)

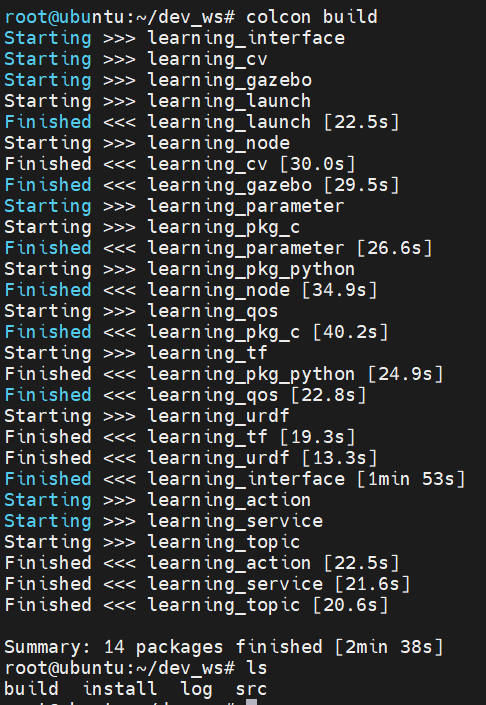
下面是一个非线性可分的例子：

import numpy as np
plot.close()
dotNum = 50
x1 = np.random.rand(dotNum) * 2 - np.ones(dotNum)
x2 = np.random.rand(dotNum) - 0.5 * np.ones(dotNum)
y1 = np.append(np.sqrt(1 - x1 ** 2), -1 * np.sqrt(1 - x1 ** 2))
x1 = np.append(x1, x1)
y2 = np.append(np.sqrt(0.25 - x2 ** 2), -1 * np.sqrt(0.25 - x2 ** 2))
x2 = np.append(x2, x2)
fig, ax = plot.subplots(figsize=figSize)
ax.axis([-1.5, 1.5, -1.5, 1.5])
ax.plot(x1, y1, "x")
ax.plot(x2, y2, "o")

问题引入

对于一个线性可分的数据集，存在着多条线段均可以达到划分数据集的目的，那条直线的分类效果最好？

要找到最好，我们首先要知道什么叫做好。

Vapnik定义了性能指标：间隔。

一些定义

• 数据集：输入$X=[x_1,x_2,...,x_n]$，输出 Y = [ y 1 , y 2 , . . . , y n ] , y i ∈ { − 1 , 1 } Y=[y_1, y_2, ..., y_n], y_i\in\{-1, 1\} Y=[y1​,y2​,...,yn​],yi​∈{−1,1}。
• 支持向量：将划分线分别向两侧平移后首次经过的数据向量集合。
• 间隔：将划分线分别向两侧移动至首次经过数据时，移动后形成的两条线之间的距离。
• 线性模型：$W^{T}x+b=0$
• 线性可分：$\exists W,b$使得$y_i(W^T{x}_i+b)\ge 0,1\le i\le n,i\in Z$

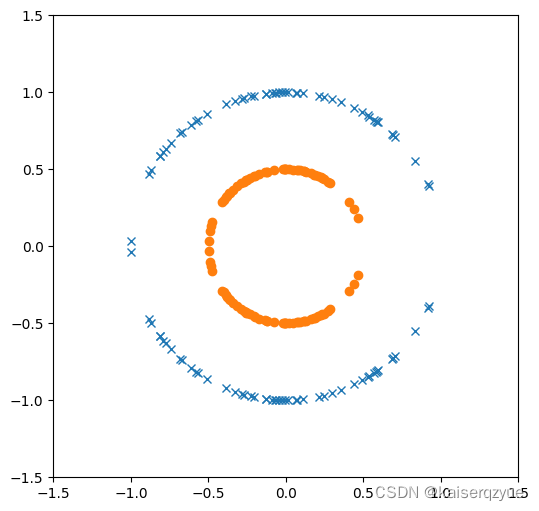
在下图中，上下两侧经过的点是支持向量，而上下两条直线之间的距离即间隔。

Vapnik认为间隔越大的直线越能够抵抗噪声的影响，因此Vapnik希望在能够划分数据集的直线中找到使间隔最大的那一条。

从下图中我们不难发现间隔最大的直线有无数条，而这无数条直线中我们只需要找到支持向量到直线距离相同的那一条（即中间那条直线）即可，这样能够尽可能的区分两类样本。

plot.close()
x1 = []
x2 = []
y1 = []
y2 = []
dotNum = 20
for i in range(dotNum):
    x1.append(random() * 1 + 4.5 - 0.5)
    x2.append(random() * 1 + 4.5 + 0.5)
    y1.append(x1[-1] + random() * 1 + 0.5)
    y2.append(x2[-1] - random() * 1 - 0.5)
line1X = [3, 7]
line1Y = [2, 8]
def dotDis2Line(dot, line):
    a = (line[1][1] - line[1][0]) / (line[0][1] - line[0][0])
    b = -1
    c = a * (-line[0][0]) + line[1][0]
    return np.abs(a * dot[0] + b * dot[1] + c) / np.sqrt(a ** 2 + b ** 2)
def moveDis2Dot(x, y, line):   
    d = -1
    for i in range(len(x)):
        if d == -1 or d > dotDis2Line([x[i], y[i]], line):
            d = dotDis2Line([x[i], y[i]], line)
    return d
d1 = moveDis2Dot(x1, y1, [line1X, line1Y])
d2 = moveDis2Dot(x2, y2, [line1X, line1Y])
print(d1, d2)
line2X = line1X
line2Y = line1Y + d1 / ((line1X[1] - line1X[0]) / (np.sqrt((line1X[1] - line1X[0]) ** 2 + (line1Y[1] - line1Y[0]) ** 2)))
line3X = line1X
line3Y = line1Y - d2 / ((line1X[1] - line1X[0]) / (np.sqrt((line1X[1] - line1X[0]) ** 2 + (line1Y[1] - line1Y[0]) ** 2)))
fig, ax = plot.subplots(figsize=figSize)
ax.axis([3.5, 6.5, 2, 8])
ax.plot(x1, y1, "x")
ax.plot(x2, y2, "o")
ax.plot(line1X, line1Y, linewidth = 1)
ax.plot(line2X, line2Y, linewidth = 1)
ax.plot(line3X, line3Y, linewidth = 1)

SVM的数学推导

复习两条知识：

• $W^{T}x+b=0$与$a{W}^{T}x+ab=0,\forall a\ne 0$为同一个（超）平面
• 欧式空间中点到（超）平面（直线）的距离：$d=\frac{|W^{T}x+b|}{\parallel W\parallel }$

有了上面的知识我们便可以写出SVM的数学模型：
$$\begin{gathered} maxd=\frac{|W^T{x}_i+b|}{\parallel W\parallel },x_{i}isSVs.t. \\ {y}_i(W^T{x}_i+b)\ge 0,1\le i\le n,i\in Z \\ {W}^T{x}_i=W^T{x}_j,x_{i}and{x}_{j}areanySV \end{gathered}$$
上面的式子并不简单，因为我们不能很好的确定那些向量是支持向量。

不过，对于任何一个线性模型，我们总可以用$a$去放缩支持向量到线性模型的距离，也就是：$\exists a,a|W^T{x}_i+b|=1,x_{i}isSV$。

而$W^{T}x+b=0$与$a{W}^{T}x+ab=0,\forall a\ne 0$为同一个（超）平面（直线），我们只需要求出$a{W}^{T}x+ab=0,\forall a\ne 0$即可。因此，我们可以对上面的式子进行如下整理：
$$\begin{gathered} min\frac{1}{2}{\parallel W\parallel }^{2}s.t. \\ {y}_i(W^T{x}_i+b)\ge 1,1\le i\le n,i\in Z \end{gathered}$$
上面的优化问题显然是一个凸优化，可以通过最优化理论学习到的知识找到最优解。

非线性可分模型

我们只需要在原优化问题中引入松弛变量$ϵ$便可继续求解$W,b$，即：
$$\begin{gathered} min\frac{1}{2}{\parallel W\parallel }^2+C\sum _{i=1}^n{ϵ}_{i}s.t. \\ {y}_i(W^T{x}_i+b)\ge 1-{ϵ}_i,1\le i\le n,i\in Z \\ {ϵ}_i\ge 0,1\le i\le n,i\in Z \end{gathered}$$
上面的问题依然是一个凸优化，但是我们不难发现，即使我们求出$W,b$，我们依然不能通过$Wx+b=0$对非线性可分数据集进行划分。

如何解决？升维，如果一个数据集在低维非线性可分，其在高维可能线性可分。

升维如何通过数学表示？函数。

下面给出另一个非线性可分的例子（异或问题）：

plot.close()
dotNum = 10
delta = 0.05
x1 =  np.random.rand(dotNum) + delta
y1 =  np.random.rand(dotNum) + delta
x2 = (np.random.rand(dotNum) + delta) * -1
y2 = (np.random.rand(dotNum) + delta) * -1
x3 =  np.random.rand(dotNum) + delta
y3 = (np.random.rand(dotNum) + delta) * -1
x4 = (np.random.rand(dotNum) + delta) * -1
y4 =  np.random.rand(dotNum) + delta
fig, ax = plot.subplots(figsize=figSize)
ax.plot(x1, y1, "x", color = "red")
ax.plot(x2, y2, "x", color = "red")
ax.plot(x3, y3, "o", color = "blue")
ax.plot(x4, y4, "o", color = "blue")

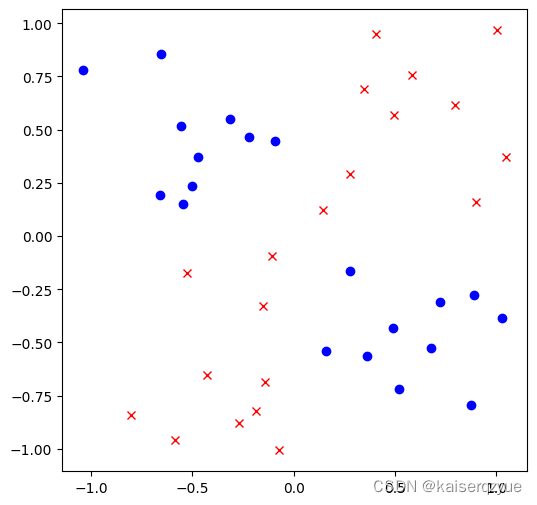
上面的例子显然非线性可分，不过如果我们通过升维函数：$\Phi (x,y)=(x,y,x\times y)$便可以获得三维坐标系下的一个线性可分数据集。

其中$z\ge 0$的是一类，$z<0$的是一类。

plot.close()
def upgrageXOR(x):
    return x[0] * x[1]
z1 = list(map(upgrageXOR, zip(x1, y1)))
z2 = list(map(upgrageXOR, zip(x2, y2)))
z3 = list(map(upgrageXOR, zip(x3, y3)))
z4 = list(map(upgrageXOR, zip(x4, y4)))
fig = plot.figure(figsize = figSize)
ax = plot.axes(projection = '3d')
partSlice = slice(0, 5, 1)
ax.scatter3D(x1, y1, z1, color = "red")
ax.scatter3D(x2, y2, z2, color = "red")
ax.scatter3D(x3, y3, z3, color = "blue")
ax.scatter3D(x4, y4, z4, color = "blue")
print(z1[partSlice], z2[partSlice], z3[partSlice], z4[partSlice], sep = "\n")

[0.239201108785093, 0.017559350544461505, 0.08023209278548173, 0.14450350214058533, 0.4912453255956246]
[0.5598293060799046, 0.04942993213533571, 0.23619320598941207, 0.2792950680234368, 0.010465888992148398]
[-0.21178774554679936, -0.39726697761636637, -0.20384691182268425, -0.6917409633280558, -0.37480972879922647]
[-0.28958407125871255, -0.08269375663158536, -0.8102547901685642, -0.12668636290350974, -0.17468973945750135]

另一个问题，高维一定线性可分吗？

已经有定理证明随着维度的提升，新的数据集线性可分的概率单调不减，且线性可分的概率收敛于$1$。

也就是说我们只要找到一个无穷升维函数，便一定可以将一个非线性可分的数据集化成线性可分的数据集。

如果假设我们现在已经找到了这样的$\Phi$，那么我们的优化问题便可以写成如下的形式：
$$\begin{gathered} min\frac{1}{2}{\parallel W\parallel }^2+C\sum _{i=1}^n{ϵ}_{i}s.t. \\ {y}_i(W^T\Phi (x_i)+b)\ge 1-{ϵ}_i,1\le i\le n,i\in Z \\ {ϵ}_i\ge 0,1\le i\le n,i\in Z \end{gathered}$$
即使让$C$等于$0$上面优化问题依然存在解，不过此时$C{\sum }_{i=1}^n{ϵ}_i$的作用是作为正则项防止出现过拟合的情况。

Kernel Function

新的问题出现了，如何找到$\Phi$使得变换后的数据集是线性可分的？

事实上，找到这样的$\Phi$是非常困难的，我们似乎从一个死胡同走到了另一个死胡同。

真的没有办法了吗？

非也，找不到$\Phi$，我们去找一个其他Kernel Function。

事实上，有下面的定理成立：

我们并不需要找到一个$\Phi$，只需要找到一个$K$，其满足$K(x_1,x_2)=\Phi (x_1{)}^T\Phi (x_2)$，这样的$K$依然可以求解上述优化问题。

新的问题又出现了，这样的$K$一定能找到吗？

是的，这样的$K$一定能找到，真是踏破铁鞋无觅处，得来全不费工夫。

实际上，若一个$K$，满足以下两点：

• $K(x_1,x_2)=K(x_2,x_1)$
• $\forall c_i,x_i,i\in [1,n],i\in Z,都有{\sum }_{i=1}^n{\sum }_{j=1}^n{c}_i{c}_{j}K(x_i,x_j)\ge 0$

则这样的$K$即满足$K(x_1,x_2)=\Phi (x_1{)}^T\Phi (x_2)$，其中$\Phi$是一个无限升维函数。

常用的两个核函数：

• $K(x_1,x_2)=e^{-\frac{\parallel x_1-x_2{\parallel }^2}{2{\sigma }^2}}$
• $K(x_1,x_2)=(x_1^T{x}_2+1{)}^d$

有了核函数，就可以通过解决对偶问题来解决原问题了（实际上应该是原问题不好解决，尝试解决对偶问题发现可以通过核函数求解对偶问题）。

相信大家都学习过最优化理论这门课程，那么写出上述问题的对偶问题应该不是难事。

完了最优化理论课程上只讲了线性对偶问题，非线性的对偶问题没有涉及。讲了，但只讲了一点点。

对偶问题

对于一个优化问题：
$$\begin{gathered} minf(W)s.t. \\ {g}_i(W)\le 0,i\in [1,k],i\in Z \\ {h}_i(W)=0,,i\in [1,k],i\in Z \end{gathered}$$
定义$L(W,\alpha ,\beta )=f(W)+{\sum }_{i=1}^k{\alpha }_i{g}_i(W)+{\sum }_{i=1}^m{\beta }_i{h}_i(W)$，则其对偶问题如下：
$$\begin{gathered} max\Theta (\alpha ,\beta )=\underset{W}{\inf }L(W,\alpha ,\beta )s.t. \\ {\alpha }_i\ge 0,i\in [1,k],i\in Z \\ {\beta }_i\ge 0,,i\in [1,k],i\in Z \end{gathered}$$
这里的对偶问题与最优化理论课程中介绍的线性对偶问题有着一些相似的定理。

$\forall W^{\ast },{\alpha }^{\ast },{\beta }^{\ast }$是各自问题的可行解，则有$f(W^{\ast })\ge \Theta ({\alpha }^{\ast },{\beta }^{\ast })$，证明如下：
$$\Theta ({\alpha }^{\ast },{\beta }^{\ast })\le L(W^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=f(W^{\ast })+\sum _{i=1}^k{\alpha }_i{g}_i(W^{\ast })\le f(W^{\ast })\text{\hspace{1em}(1)}$$

强对偶定理：若$f(W)$为凸函数，$g_i,h_i$均为线性函数，则有$f(W^{\ast })=\Theta ({\alpha }^{\ast },{\beta }^{\ast })$。

不难发现若强对偶定理成立，那么$(1)$中的不等号全部要变成等号，于是可以得到$K.K.T.$条件：${\alpha }_i{g}_i(W^{\ast })=0,i\in [1,k],i\in Z$

要写出$SVM$数学问题的对偶形式，我们首先要将原优化问题化成与上面对应的标准形式：
$$\begin{gathered} min\frac{1}{2}{\parallel W\parallel }^2-C\sum _{i=1}^n{ϵ}_{i}s.t. \\ -y_i\Phi (x_i{)}^{T}W-y_{i}b+1+{ϵ}_i\le 0,1\le i\le n,i\in Z \\ {ϵ}_i\le 0,1\le i\le n,i\in Z \end{gathered}$$
于是不难写出其对偶问题如下：
$$\begin{gathered} max\Theta (\alpha ,\beta )=\underset{ϵ,W,b}{\inf }\left\{\frac{1}{2}{\parallel W\parallel }^2-C\sum _{i=1}^n{ϵ}_i+\sum _{i=1}^n{\alpha }_i(-y_i\Phi (x_i{)}^{T}W-y_{i}b+1+{ϵ}_i)+\sum _{i=1}^n{\beta }_i{ϵ}_i\right\}s.t. \\ {\alpha }_i\ge 0,1\le i\le n,i\in Z \\ {\beta }_i\ge 0,1\le i\le n,i\in Z \end{gathered}$$

对偶问题的求解

我们不难发现，上述问题满足强对偶定理，于是我们尝试通过$K.K.T.$点求解对偶问题。

我们首先解决inf，对于凸函数而言，只需要其偏导数均等于0即可，因此：
$$\{\begin{array}{rl}& \frac{\partial L}{\partial W}=W-\sum _{i=1}^n{\alpha }_i{y}_i\Phi (x_i)=0\\ & \frac{\partial L}{\partial b_i}={\alpha }_i+{\beta }_i-C=0,1\le i\le n,i\in Z\\ & \frac{\partial L}{\partial {ϵ}_i}=\sum _{i=1}^n{\alpha }_i{y}_i=0,1\le i\le n,i\in Z\end{array}$$
我们稍加整理便可以得到：
$$\{\begin{array}{rl}& W=\sum _{i=1}^n{\alpha }_i{y}_i\Phi (x_i)\\ & {\alpha }_i+{\beta }_i=C,1\le i\le n,i\in Z\\ & \sum _{i=1}^n{\alpha }_i{y}_i=0,1\le i\le n,i\in Z\end{array}$$
将三个式子带入到$\Theta (\alpha ,\beta )$中，便可以将对偶问题进行化简得到：
$$\begin{gathered} max\Theta (\alpha ,\beta )=\Theta (\alpha )=\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{i=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\Phi }^T(x_i)\Phi (x_j)=\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{i=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)s.t. \\ {\alpha }_i\ge 0,1\le i\le n,i\in Z \\ \sum _{i=1}^n{\alpha }_i{y}_i=0,1\le i\le n,i\in Z \end{gathered}$$
我们可以通过SMO算法求解上述问题。

新的问题，我们如何通过已经求解出来的${\alpha }_i$来求解$W,b$？

似乎可以通过$W={\sum }_{i=1}^n{\alpha }_i{y}_i\Phi (x_i)$求解$W$，不过我们并不知道$\Phi (x_i)$。

事实上，我们没有必要求解$W$，对于测试数据，我们只需要知道$W^T\Phi (x)$：
$$W^T\Phi (x)=(\sum _{i=1}^n{\alpha }_i{y}_i\Phi (x_i){)}^T\Phi (x)=\sum _{i=1}^n{\alpha }_i{y}_i{\Phi }^T(x_i)\Phi (x)=\sum _{i=1}^n{\alpha }_i{y}_{i}K(x_i,x)$$
因此我们只需要求解$b$即可。

由$K.K.T.$条件可以知道:
$$\begin{gathered} {\beta }_i{ϵ}_i=0,1\le i\le n,i\in Z \\ {\alpha }_i(-y_i\Phi (x_i{)}^{T}W-y_{i}b+1+{ϵ}_i)=0,1\le i\le n,i\in Z \end{gathered}$$
我们可以让${\beta }_i\ne 0$,则${ϵ}_i=0$,若${\alpha }_i\ne 0$则有：
$$b=\frac{1-y_i\Phi (x_i{)}^{T}W}{y_i}$$
我们可以选择多个${\alpha }_i\ne 0$算出多个$b$求平均值作为最终的$b$。

最后给出一个例子SVM求解非线性可分的例子（之前的异或问题）：

from sklearn import svm
from sklearn.metrics import accuracy_score

model = svm.SVC(C = 1, kernel = "rbf", gamma = "scale")
trainDataLen = 100
x1 =  np.random.rand(trainDataLen) + delta * np.ones(trainDataLen)
y1 =  np.random.rand(trainDataLen) + delta * np.ones(trainDataLen)
x2 = (np.random.rand(trainDataLen) + delta * np.ones(trainDataLen)) * -1
y2 = (np.random.rand(trainDataLen) + delta * np.ones(trainDataLen)) * -1
x3 =  np.random.rand(trainDataLen) + delta * np.ones(trainDataLen)
y3 = (np.random.rand(trainDataLen) + delta * np.ones(trainDataLen)) * -1
x4 = (np.random.rand(trainDataLen) + delta * np.ones(trainDataLen)) * -1
y4 =  np.random.rand(trainDataLen) + delta * np.ones(trainDataLen)
feature = []
for i in range(trainDataLen):
    feature.append([x1[i], y1[i]])
    feature.append([x2[i], y2[i]])
    feature.append([x3[i], y3[i]])
    feature.append([x4[i], y4[i]])
label = [1, 1, -1, -1] * trainDataLen
testDataLen = 1000
testFeature  = list(zip( np.random.rand(testDataLen) + delta * np.ones(testDataLen),
                         np.random.rand(testDataLen) + delta * np.ones(testDataLen)))
testFeature += list(zip((np.random.rand(testDataLen) + delta * np.ones(testDataLen)) * -1,
                        (np.random.rand(testDataLen) + delta * np.ones(testDataLen)) * -1))
testFeature += list(zip( np.random.rand(testDataLen) + delta * np.ones(testDataLen),
                        (np.random.rand(testDataLen) + delta * np.ones(testDataLen)) * -1))
testFeature += list(zip((np.random.rand(testDataLen) + delta * np.ones(testDataLen)) * -1,
                         np.random.rand(testDataLen) + delta * np.ones(testDataLen)))
testLabel = [1] * testDataLen * 2 + [-1] * testDataLen * 2
testDataLen *= 4

fig, ax = plot.subplots(figsize=figSize)
model.fit(feature, label)
predictLabel = list(model.predict(testFeature))
print("testLabel:   ", testLabel[:10])
print("predictLabel:", predictLabel[:10])
print("accuracy ratio:", accuracy_score(testLabel, predictLabel))
class1X = []
class1Y = []
class2X = []
class2Y = []
for i in range(testDataLen):
    if predictLabel[i] == 1:
        class1X.append(testFeature[i][0])
        class1Y.append(testFeature[i][1])
    else:
        class2X.append(testFeature[i][0])
        class2Y.append(testFeature[i][1])
ax.plot(class1X, class1Y, "x")
ax.plot(class2X, class2Y, "o")

testLabel:    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
predictLabel: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
accuracy ratio: 1.0

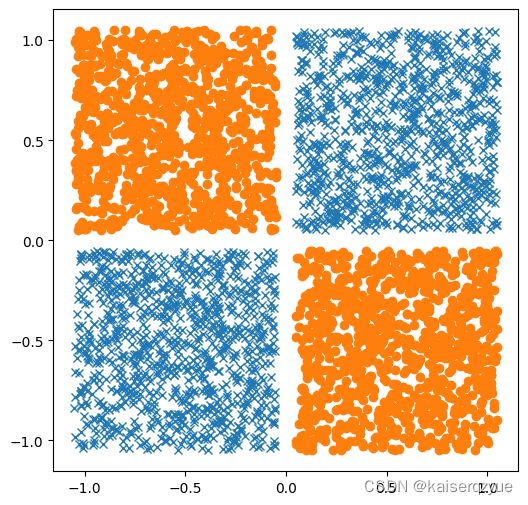
在介绍线性可分的情况下，我们只说了优化问题是一个凸优化，没有给出具体的求解算法。

实际上，对于线性可分的数据集，也可以通过对偶问题求解，相当于使用“核函数”$K(x_i,x_j)=x_i^T{x}_j$（严格来说不是核函数，其不一定满足半正定性）。这样就可以同样使用SMO算法求解线性可分的情况。

处理多类别数据

一个SVM可以解决二分类问题，那么对于一个N分类问题，我们使用多个个SVM即可进行分类。

以三分类问题为例

一类对其他类方法（构造$N$个SVM）：
$$\begin{gathered} SVM1:(C_2{C}_3)v.s.(C1) \\ SVM2:(C_1{C}_3)v.s.(C2) \\ SVM3:(C_1{C}_2)v.s.(C3) \end{gathered}$$
一类对另一类方法（构造$C_N^2$个SVM）：
$$\begin{gathered} SVM1:(C_1)v.s.(C2) \\ SVM2:(C_1)v.s.(C3) \\ SVM3:(C_2)v.s.(C3) \end{gathered}$$
其他的方法（构造$N-1$个SVM）：
$$\begin{array}{rl}& SVM1:(C_2{C}_3)v.s.(C1)\\ & SVM2:(C_3)v.s.(C2)\end{array}$$

参考

【SVM支持向量机】讲解

scikit-learn

matplotlib