35 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。请必须使用时间复杂度为 O(log n) 的算法。
基础写法!!!牢记!!!
第一个只适用与一个目标值的情况,第二个适用于多个目标值靠左取的情况(要靠右取可以找target+1获得下标值-1);
class Solution(object): def searchInsert(self, nums, target): """ :type nums: List[int] :type target: int :rtype: int """ left, right = 0, len(nums)-1 while left <= right: mid = (left+right)//2 if target == nums[mid]:return mid elif target < nums[mid]: right = mid-1 else: left = mid+1 return left def lower_bound(nums, target): left, right = 0, len(nums) - 1 # 闭区间 [left, right] while left <= right: mid = (left + right) // 2 if nums[mid] < target: left = mid + 1 # 范围缩小到 [mid+1, right] else: right = mid - 1 # 范围缩小到 [left, mid-1] return left
74 搜索二维矩阵
给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
方法一:二分先找列再找行 定列的时候要靠近小值(取down)
或者将二维矩阵拉成一维矩阵然后同题35 时间复杂度相同O(logm+logn)
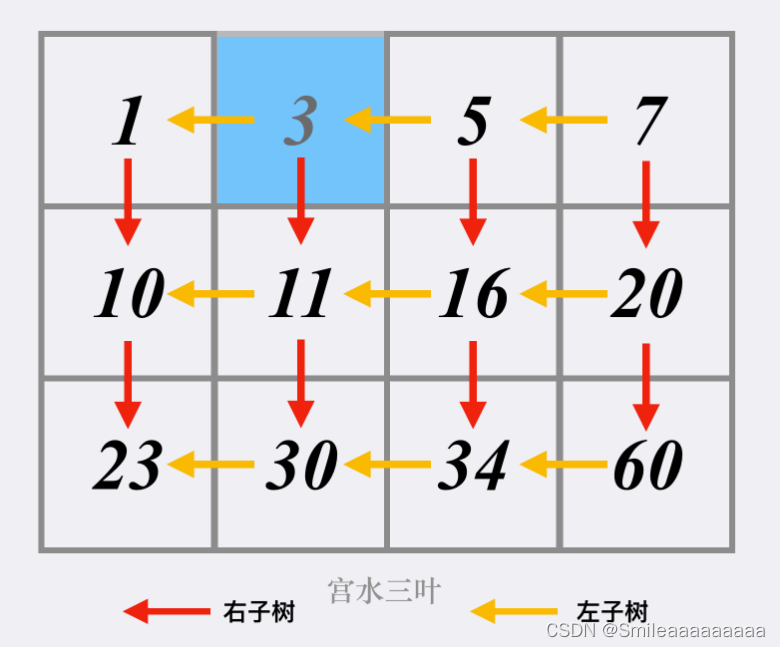
class Solution(object): def searchMatrix(self, matrix, target): """ :type matrix: List[List[int]] :type target: int :rtype: bool """ up, down = 0, len(matrix)-1 while up <= down: mid = (up+down)//2 if target == matrix[mid][0]: return True elif target < matrix[mid][0]: down = mid-1 else: up = mid+1 left, right = 0, len(matrix[0])-1 while left <= right: mid = (left+right)//2 if target == matrix[down][mid]: return True elif target < matrix[down][mid]: right = mid-1 else: left = mid+1 return False方法二:满足题目规定的二维矩阵可以看成一棵二叉搜索树 时间复杂度O(m+n)
class Solution: def searchMatrix(self, matrix, target): m, n = len(matrix), len(matrix[0]) x, y = 0, n - 1 while x < m and y >= 0: if matrix[x][y] > target: y -= 1 elif matrix[x][y] < target: x += 1 else: return True return False
34 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target,返回 [-1, -1]。你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
两遍二分查找,第一遍找target,第二遍找target+1,都靠左取;
不存在目标值情况:目标值过小/大,idx1=0/len(nums)
目标值没出现:nums[idx1] != target (可以和idx1=0合并)
class Solution(object): def searchRange(self, nums, target): """ :type nums: List[int] :type target: int :rtype: List[int] """ left, right = 0, len(nums)-1 while left <= right: mid = (left+right)//2 if nums[mid] < target: left = mid+1 else: right = mid-1 idx1 = left left, right = 0, len(nums)-1 while left <= right: mid = (left+right)//2 if nums[mid] < target+1: left = mid+1 else: right = mid-1 idx2 = left-1 if idx1 == len(nums) or nums[idx1] != target: return [-1, -1] else: return [idx1, idx2]
33 搜索旋转排列数组
整数数组 nums 按升序排列,数组中的值 互不相同 。在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
二分出一侧排序正确的区域,若target在这个区域里,正常查找,若在排序不正确的区域里,继续二分;
因为目标值仅出现一次,可提前判断;
找不到递增区间时终止循环;
class Solution(object): def search(self, nums, target): """ :type nums: List[int] :type target: int :rtype: int """ left, right = 0, len(nums)-1 while left <= right: mid = (left+right)//2 if nums[mid] == target: return mid elif nums[left] == target: return left elif nums[right] == target: return right if nums[left] < nums[mid] : # [left, mid]排序正确 if nums[mid] > target and nums[left] < target: # target在[left, mid]内 right = mid - 1 else: left = mid + 1 elif nums[mid] < nums[right]: # [mid, right]排序正确 if nums[mid] < target and nums[right] > target: # target在[mid, right]内 left = mid + 1 else: right = mid - 1 else: return -1 if not nums or nums[left] != target: return -1 else: return left
153 寻找排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
假设旋转k次,则数组为 [a[n-k],a[n-k+1],...,a[0],...,a[n-k-1]] 一次二分
情况一:nums[left] < nums[mid] < nums[right] 最小值为 nums[left]
情况二:若左侧排序正确最小值只可能在右侧区间 搜索区间为[mid+1,right]
情况三:同理右侧排序正确则最小值只可能在左侧区间 搜索区间为[left,mid] 注意mid是右侧排序正确区间的最小值,也要放在搜索范围里;
当找不到递增序列时,取两个数的最小值;
class Solution(object): def findMin(self, nums): """ :type nums: List[int] :rtype: int """ left, right = 0, len(nums)-1 while left <= right: mid = (left+right)//2 if nums[left] < nums[mid] and nums[mid] < nums[right]: return nums[left] elif nums[left] < nums[mid] and nums[mid] > nums[right]: # [left, mid]排序正确 left = mid + 1 elif nums[left] > nums[mid] and nums[mid] < nums[right]: # [mid, right]排序正确 right = mid else: return min(nums[left], nums[right])
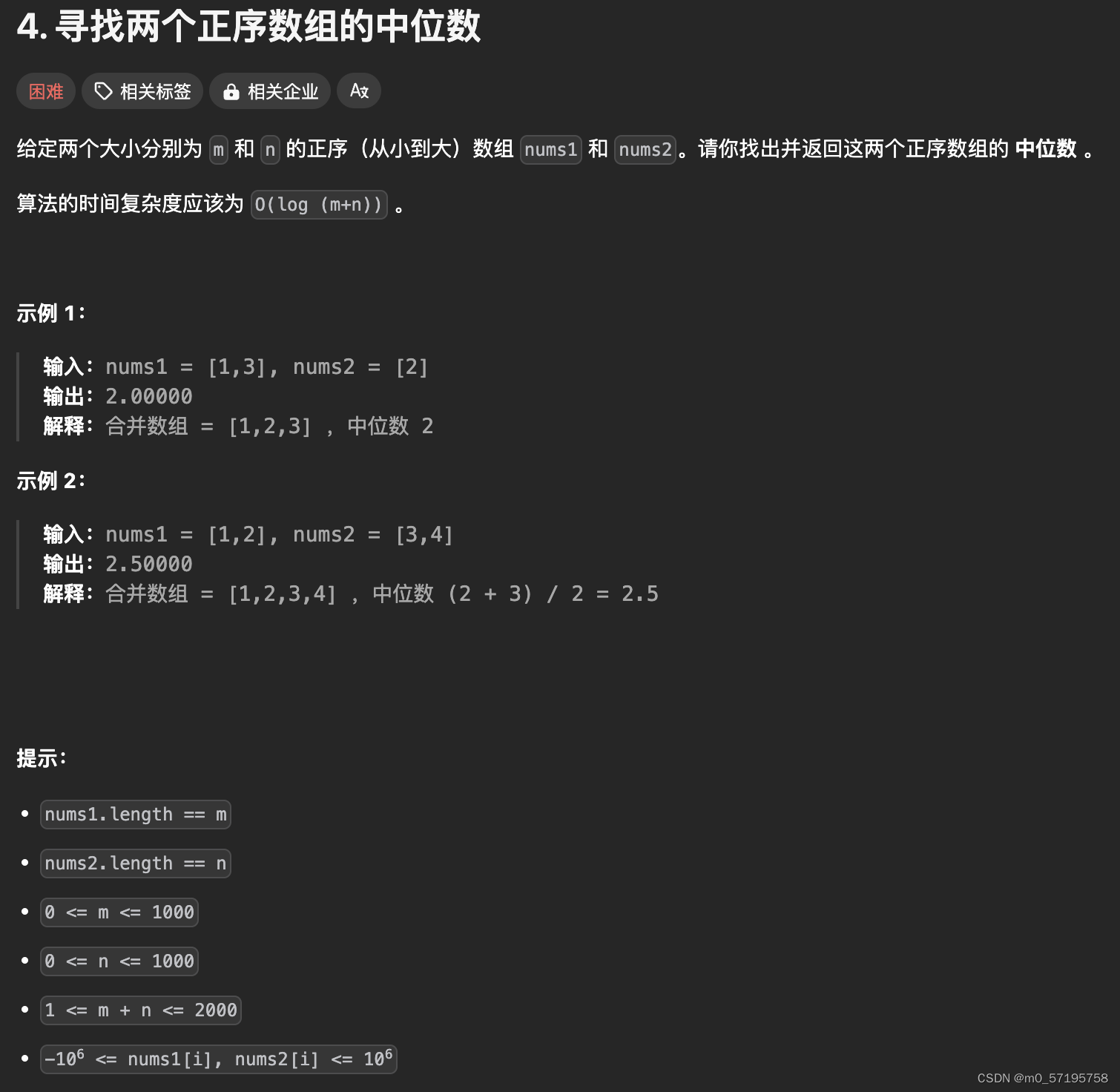
4 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。算法的时间复杂度应该为 O(log (m+n)) 。
方法一:合并两个有序数组后取中间位置的元素; 时间复杂度O(m+n) 空间复杂度O(m+n)
将问题转换为两个有序数组中取第k小的数 k=(m+n)/2 or (m+n)/2+1
方法二:使用双指针,每次移动较小值的指针至移动k次; 时间复杂度O(m+n) 空间复杂度O(1)
方法三: 比较nums1[k/2-1]和nums2[k/2-1],对于二者中的较小值(假设nums1[k/2-1]),其在合并数组中的下标一定小于(k/2-1)*2+1<k,就不可能是目标值,此时nums1[0:k/2]也不可能含有目标值;随后根据排除掉的长度更新k后继续循环;
终止条件:某个数组为[ ],直接返回另一个数组的第k个元素;
k=1,直接取两数组第一个元素的最小值;
class Solution(object): def findMedianSortedArrays(self, nums1, nums2): """ :type nums1: List[int] :type nums2: List[int] :rtype: float """ def getKthElement(k): index1, index2 = 0, 0 while True: # 特殊情况 if index1 == m: return nums2[index2 + k - 1] if index2 == n: return nums1[index1 + k - 1] if k == 1: return min(nums1[index1], nums2[index2]) # 正常情况 newIndex1 = min(index1 + k // 2 - 1, m - 1) # 防止越界 newIndex2 = min(index2 + k // 2 - 1, n - 1) pivot1, pivot2 = nums1[newIndex1], nums2[newIndex2] if pivot1 <= pivot2: k -= newIndex1 - index1 + 1 index1 = newIndex1 + 1 else: k -= newIndex2 - index2 + 1 index2 = newIndex2 + 1 m, n = len(nums1), len(nums2) totalLength = m + n if totalLength % 2 == 1: return getKthElement((totalLength + 1) // 2) else: return (getKthElement(totalLength // 2) + getKthElement(totalLength // 2 + 1)) / 2.