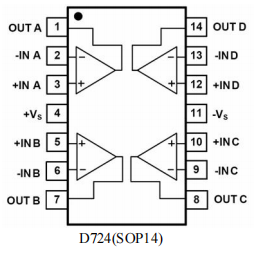
本文重点
我们上一节课程中学习了如何利用神经网络对图片中的对象进行定位,也就是通过输出四个参数值bx、by、bℎ和bw给出图片中对象的边界框。
本节课程我们学习特征点的检测,神经网络可以通过输出图片中对象的特征点的(x,y)坐标来实现对目标特征的识别,我们看几个例子。
例子
比如我们想要识别一个人眼角的具体位置,眼角可以通过一个具体坐标(x,y)来确定。那么我们可以建立一个有两个输出单元的神经网络,分别输出两个数字和。作为眼角的坐标值。
如果你想知道两只眼睛的四个眼角的具体位置,那么从左到右,依次用四个特征点来表示这四个眼角。对神经网络稍做些修改,输出第一个特征点(l1x,l1y),第二个特征点(l2x,l2y),依此类推,这四个脸部特征点的位置就可以通过神经网络输出了。
如果我们想要输出人脸中的所有的特征点也是可以的,比如据嘴部的关键点,取鼻子周围的关键特征点等等。
那么针对特征点检测的样本标签应该如何设置呢?
准备一个卷积网络和一些特征集,将人脸图片输入卷积网络,卷积网络有129个输出,第一个输出 1 或 0,1 表示有人脸,0 表示没有人脸,然后输出(l1x,l1y)……直到(l64x,l64y),假如我们检测64个特征点。