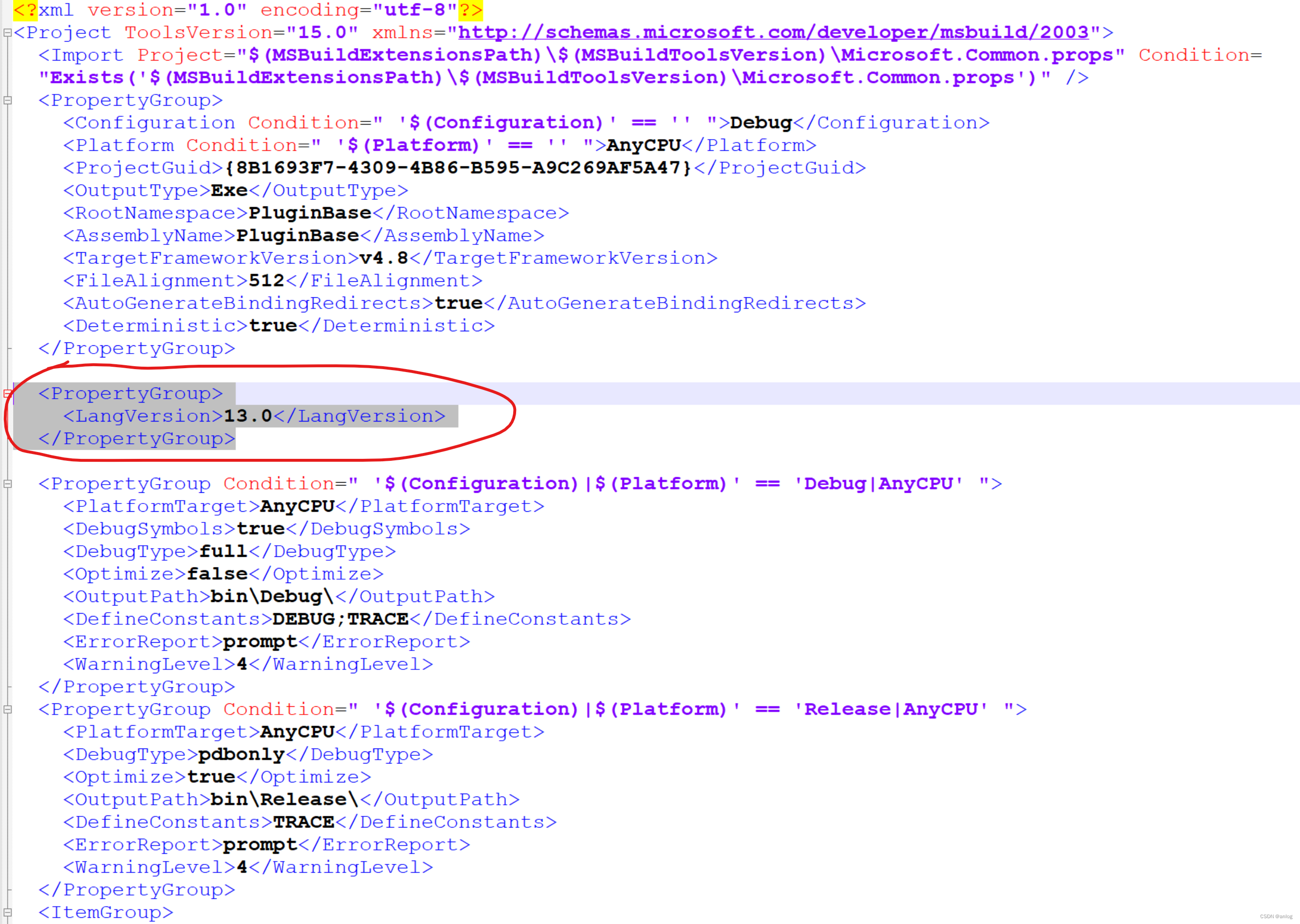
参考连接:在c# 7.3中不可用,请使用8.0或更高的语言版本_功能“可为 null 的引用类型”在 c# 7.3 中不可用。请使用 8.0 或更高的语言版本-CSDN博客![]() https://blog.csdn.net/liangyely/article/details/106163660
https://blog.csdn.net/liangyely/article/details/106163660
[踩坑记录] 某功能在C#7.3中不可用,请使用 8.0 或更高的语言版本 (通用解决方案)_无效的 nullable 值: c# 7.3 的“enable”。请使用语言版本 8.0 或更高版本-CSDN博客![]() https://blog.csdn.net/m0_46555380/article/details/113706200
https://blog.csdn.net/m0_46555380/article/details/113706200
C# 语言版本控制 - C# 指南 - C# | Microsoft Learn![]() https://learn.microsoft.com/zh-cn/dotnet/csharp/language-reference/configure-language-version#edit-the-project-file
https://learn.microsoft.com/zh-cn/dotnet/csharp/language-reference/configure-language-version#edit-the-project-file
特此记录
anlog
2024年4月2日