---

前言

从这一篇开始我们依次介绍几种模拟信号调制的方法，包括其数学表达式，系统框图、解调方式、性能评价等。

---

一、DSB-SC的数学表示

将$m(t)$作为已调信号$s(t)$的复包络，我们可以得到第一种模拟调制方案——即双边带抑制载波调制。首先我们推导一下$s(t)$的表达式：

$s_L(t)=m(t)=\left[s(t)+j\hat{s}(t)\right]e^{-j2\pi f_{c}t}$
$s(t)=Re\left[m(t)e^{j2\pi f_{c}t}\right]=m(t)\cos 2\pi f_{c}t$

其中$A_c,f_c$分别为已调信号的幅度系数与载波频率。原信号乘上余弦信号，频域上就是将信号左右搬移到载频$f_c$处。因为我们有模拟基带信号$m(t)$为无直流分量的实信号的假设，所以我们有已调信号的频谱在载频处无冲激分量（抑制载波），并且其频谱图像分成对称的两部分，称为上下边带（双边带）。

二、DSB-SC的相干解调

通过其数学表示，我们可以很容易地得到实现的系统框图如下：

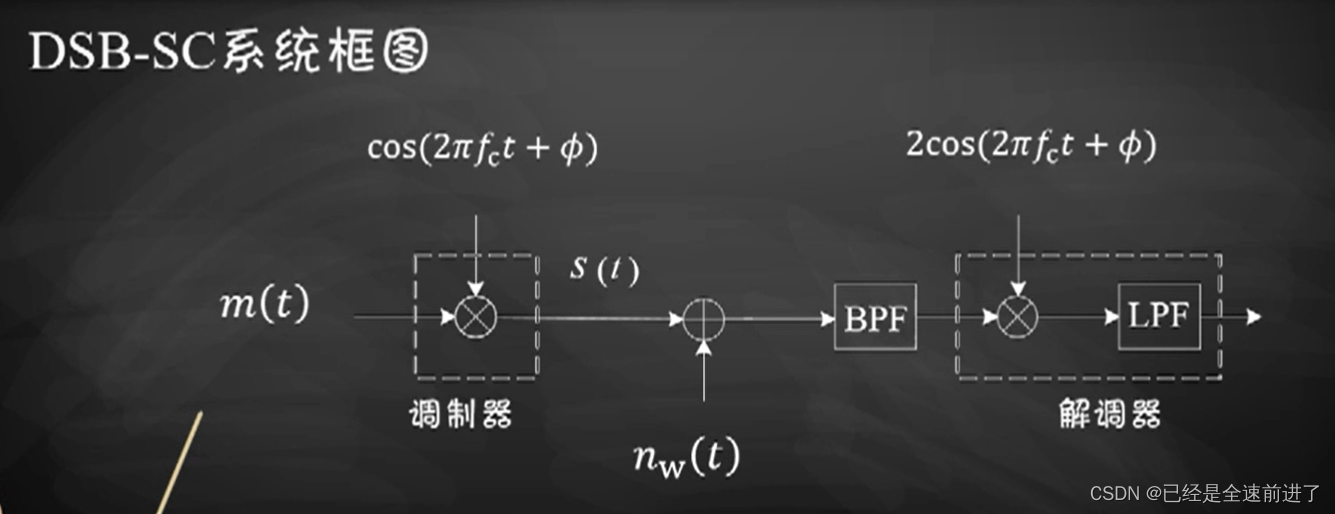
基带信号与载波信号相乘，叠加上高斯噪声后通过带通滤波器，再进行解调。这里载波信号里面的$\varphi$是随机相位。

接下来我们来看解调器，首先是将滤波后的信号乘上载波信号，这里载波信号的相位也必须和原来的完全一致（所以这种解调方式称为相干解调），然后再通过一个低通滤波器。从频域上分析，乘上余弦载波，原本的带通信号正负频率都有一部分被搬移到基带$M(f)$，另一部分搬移到两倍载频$M(f+2f_c),M(f-2f_c)$，经过低通滤波器后（滤波带宽与调制信号$m(t)$匹配），由于带通信号的假设$f_c>2W$，两倍载频的信号均被滤除，最后剩下的就是与原信号形状相同的基带信号。

接下来用数学公式进行一下推导：

$s(t)\ast 2\cos (2\pi f_{c}t+\varphi )=m(t)2{\cos }^2(2\pi f_{c}t+\varphi )$
$=m(t)+A_{c}m(t)\cos (4\pi f_{c}t)$
LPF低通滤波后
$=m(t)$

相干解调最重要的是载波同步，也叫载波恢复，即解调所用载波信号要与调制所用载波完全一致。如果不一致会怎么样呢？我们假设解调载波改用$\cos (2\pi f_{c}t+\theta )$试试：

$=m(t)2\cos (2\pi f_{c}t+\varphi )\cos (2\pi f_{c}t+\theta )$
$m(t)\left[\cos (\varphi -\theta )+\cos (4\pi f_{c}t+\varphi +\theta )\right]$
LPF低通滤波后
$=m(t)\cos (\varphi -\theta )$

可以看到，如果载波无法同步，恢复的信号将会受到随机相位的影响，从而无法稳定地解调出原信号。

三、DSB-SC的性能评价

带宽资源上，DSB-SC占用的带宽是原本基带信号带宽的两倍（因为有两个边带）。调制效率上，没有使用功率发送其他如载波信号等，不需要讨论调制效率。

解调方式上来说，只能进行相干解调，因此必须实现载波同步。

信噪比上，解调信号的功率为$P_m$,噪声功率我们需要先分析一下解调以后的噪声信号。

首先高斯白噪声通过BPF后变成带宽为2W载频为$f_c$的窄带高斯噪声$n(t)=n_c(t)\cos (2\pi f_{c}t+\varphi )-n_{s}t()\sin (2\pi f_{c}t+\varphi )$，其中W为$m(t)$的带宽。经过解调器后，输出噪声信号为：

$n_c(t)+n_c(t)\cos (4\pi f_{c}t+2\varphi )-n_s(t)\sin (4\pi f_{c}t+2\varphi )$
LPF滤波后
$=n_c(t)$

根据窄带高斯噪声的复包络$n_L(t)$的性质，我们有

$n_c(t)=Re(n_L(t))=Re(\left[n(t)+j\hat{n}(t)\right]e^{-2\pi fct+\varphi })$
$=n(t)\cos (2\pi f_{c}t+\varphi )+\hat{n}(t)\sin (2\pi f_{c}t+\varphi )$

希尔伯特变换不改变功率，任意一个信号乘上余弦信号后功率减半，因此最终得出正交分量$n_c(t)$的功率等于窄带高斯噪声$n(t)$的功率（n_s(t)也是），因此输出噪声功率为$P_n=2N_{0}W$，信噪比为$P_m/2N_{0}W$。

---

最后我们来推导一下任意一个信号乘上余弦信号后功率减半：

让信号$x(t)$乘上余弦信号$\cos 2\pi f_{c}t$：
$x(t)\cos 2\pi f_{c}t=\frac{1}{2}x(t)e^{-2\pi fct}+\frac{1}{2}x(t)e^{2\pi f_{c}t}$

可见乘上余弦进行就是将原信号频谱幅度缩小为一半然后左右搬移，功率为功率谱的积分，因此搬移不影响功率，而幅度谱缩小为一半，功率谱则缩小为原来的四分之一。从而新信号的功率

$P=\frac{1}{4}{P}_x+\frac{1}{4}{P}_x=\frac{1}{2}{P}_x$

---

总结

本文介绍了最基本最直接的调制方式——DSB-SC调制，这种调制方式需要使用相干解调。那么就有一种优化思路是将载波信号也一起发送过去，在接收端使用窄带滤波器获取该载波信号进行解调，下一篇将进行这种调制方式的讲解。