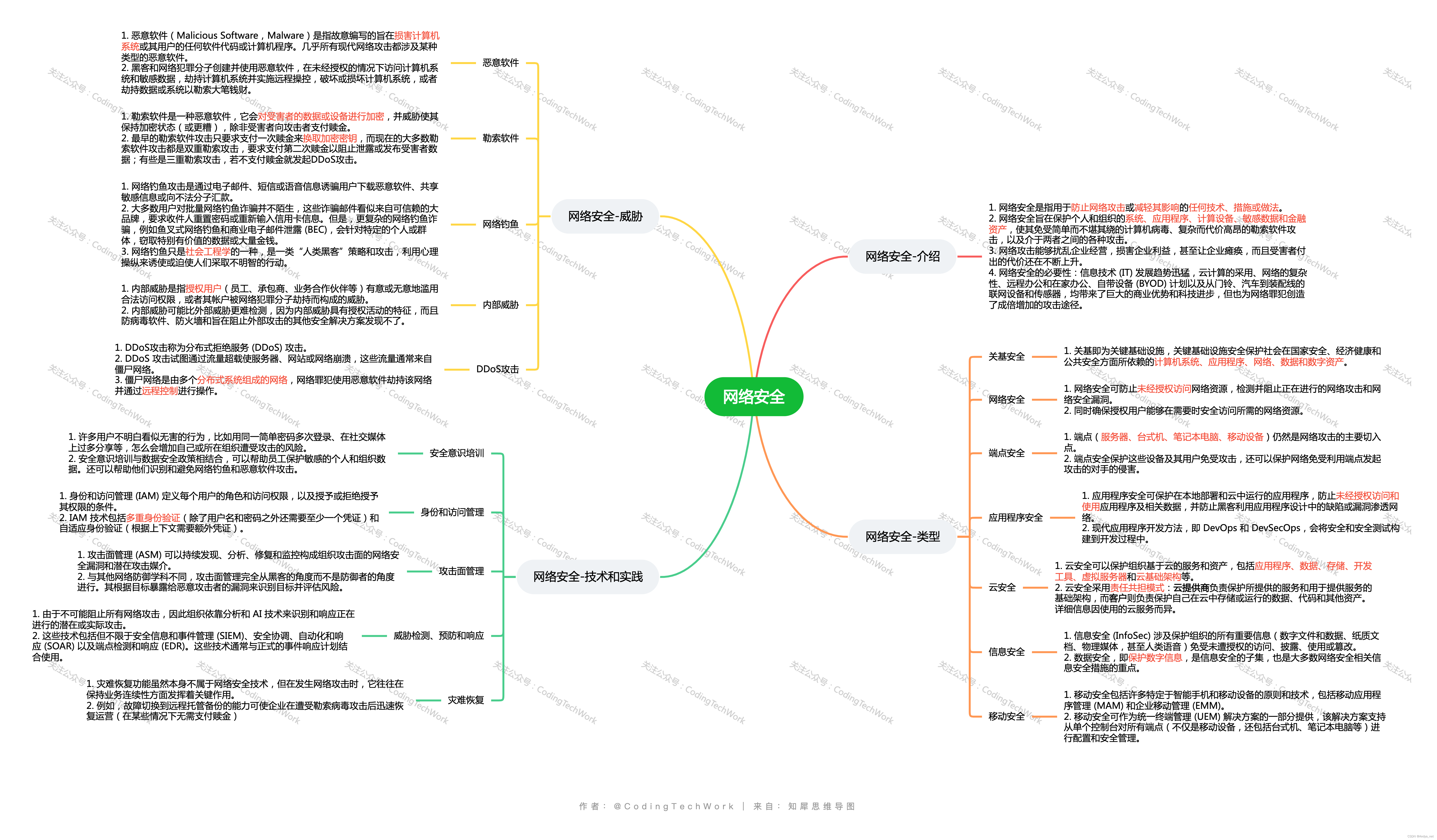
YOLOv6 是美团推出的，在这个版本里面，不再使用之前 YOLOv4 和 YOLOv5 的带 CSP 结构的 CSPDarknet-53 作为 backbone 了，而是在 RepVGG 的启发下，推出了新的 EfficientRep 作为 YOLOv6 的 backbone。

RepVGG 最重要的一点是：结构的重参数化

简单来说，在训练和推理的时候采用不同的结构，在训练的时候采用多分支结构进行训练，但是在推理的时候使用单分支，即保留了训练多分支的准确度，又兼具推理时单分支的速度。

具体来说，训练中，backbone 中使用的是 RepBlock 模块，但是在推理的时候，可以将这些 RepBlock 模块换成带 ReLU 激活函数的 3 x 3 卷积块。

RepVGG 主干在小型网络中具有更强的特征表示能力，但是随着参数和计算成本的爆炸式增长， RepVGG 在大模型中难以获得较高的性能，所以：

• 在小模型（n / t / s）中，使用 RepBlock
• 在大模型（m / l） 中，使用 CSPStackRep Block

YOLOv5 和 YOLOv6 的 backbone 对比

最左边 YOLOv5 的 backbone 我用的是最新版本的，其中 CSP 模块是 C3 模块，然后激活函数也是 SiLU的。从上面图片可以看出来，基本上，YOLOv6 大体上的结构变化不大，但是内部的 C3 模块换成了 RepBlock 模块或者是 CspStackRep Block 模块（这取决于模型的大小）。用到的 RepBlock 模块和 CspStackRep 模块的具体结构也在右边给了出来。

值得注意的是，就和前面提到的训练和推理的解耦，训练的时候，RepBlock 和 CspStackRep Block 模块内部使用的都是 RepVGG 模块，这是一种多分支结构，可以学习到更多不同的特征。但是到了推理的时候，为了提升推理的速度，将多分支的 RepVGG 换成了单分支的 RepConv 结构。

其实也可以看出来 YOLOv6 的一个比较创新的地方就是 RepVGG 模块向 RepConv 转换的一个结构重参数化。

RepVGG(train) -> RepConv(infer)

对于不同的分支，重参数化的过程不一样：

• 3x3 Conv：直接与 BN 层进行融合
• 1x1 Conv：先 padding 成 3x3 Conv，然后与 BN 层进行融合
• identity：先转换成 1x1 Conv，然后再转成 3x3 Conv，最后与 BN 层进行融合

3x3 Conv 层与 BN 层融合

RepConv 其实就是一个 3x3 卷积 + ReLU 激活函数，相比于普通的卷积块，少了其中的 BN 层，这是因为 Rep 的核心思想就是 Conv2D 与 DB 的融合，等效成一个 3x3 卷积。

我们知道：卷积 Conv2D 和 批归一化 BN 的公式如下：$$\text{Conv}(x)=W(x)+b$$$$\text{BN}(x)=\gamma \cdot \frac{(x-\text{mean})}{\sqrt[]{\text{var}}}+\beta$$按照卷积块的流程，先经过卷积层，然后是 BN 层，公式可以写成下面形式：$$\text{BN}(\text{Conv}(x))=\gamma \cdot \frac{W(x)+b-\text{mean}}{\sqrt{\text{var}}}+\beta$$化简可以得到：$$\text{BN}(\text{Conv}(x))=\frac{\gamma }{\sqrt[]{\text{var}}}\cdot W(x)+(\frac{\gamma \cdot (b-\text{mean})}{\sqrt[]{\text{var}}}+\beta )$$其实可以等价为一个卷积层：$$W_{fused}(x)=\frac{\gamma }{\sqrt[]{\text{var}}}\cdot W(x)$$$$b_{fused}=\frac{\gamma \cdot (b-\text{mean})}{\sqrt[]{\text{var}}}+\beta$$Conv 与 BN 融合的结果可以表示为：$$\text{BN}(\text{Conv}(x))=W_{fused}(x)+b_{fused}$$

这上面的计算过程中 Conv 是带 bias 的，但是现在一般来说，如果后面接的是 BN 层，Conv 是不需要带 bias 的，因为即便带了 bias，在后续的 BN 层中，也不会有什么作用，反而增加计算量。

3x3 Conv 与 1x1 Conv 融合

首先，我们知道多通道卷积：

• 卷积核的通道数 = 输入的通道数
• 卷积核的数量 = 输出的通道数
• 输入和卷积核的卷积是对应通道之间的卷积之和

所以上面的图中，输入是 3x3x2，有 2 个 channel。然后卷积核也有 2 个，每个卷积核有 2 个 channel。

所以 3x3 Conv 简化下来可以画上面那样，中间的 4 个 3x3 卷积核实际上和 RepVGG(train) -> RepConv(infer) 章节的 4 个绿色的卷积核是一样的意思。

我们知道 1x1 Conv 的卷积的计算过程如上面示意图所示，其实我们也发现了，将 1x1 Conv 周围 padding 成 0 就可以等效转换成 3x3 Conv 层了，获得和 1x1 Conv 一样的输出结果。

identity -> 1x1 Conv -> 3x3 Conv

而 identity 的分支，我们想要输入和输出是一样的，根据上面的 1x1 卷积，其实我们可以做出下面的转换

首先将 identity 转换成如上所示的 1x1 Conv，然后再转换成 3x3 Conv

identity 层就是输入直接等于输出，也即 input 中每个通道每个元素直接输出到 output 中对应的通道，用一个什么样的卷积层来等效这个操作呢，我们知道，卷积操作必须涉及要将每个通道加起来然后输出的，然后又要保证 input 中的每个通道每个元素等于 output 中，从这一点，我们可以从 PWconv 想到，只要令当前通道的卷积核参数为 1，其余的卷积核参数为 0，就可以做到；从 DWconv 中可以想到，用 conv_1x1 卷积且卷积核权重为 1，就能保证每次卷积不改变输入，因此， identity 可以等效成如下的 conv_1x1 的卷积形式：

参考文章：

• 【笔记】YOLOv7重参数化(RepConV)原理+代码
  
• 【YOLO系列】YOLOv6论文超详细解读（翻译 ＋学习笔记）
  
• 大道至简！深度解读CVPR2021论文RepVGG