C语言数据结构易错知识点（6）（快速排序、归并排序、计数排序）

news2024/11/28 0:41:55

快速排序属于交换排序，交换排序还有冒泡排序，这个太简单了，这里就不再讲解。

归并排序和快速排序都是采用分治法实现的排序，理解它们对分支思想的感悟会更深。

计数排序属于非比较排序，在数据集中的情况下可以考虑使用。这时效率也比较高。

 

下面讲解一下这三种排序在代码实现上易错的地方：

一、快速排序

快速排序通过每趟排序确定一个数的最终位置最终实现将数组变得有序的功能。主要有三种方法，第一种方法偏向常规，第二种方法是双指针法，第三种方法是非递归法，除此之外，还有一些优化的方案，如挖坑法，随机确定key，三数取中，后面代码实现上会简要说明。

方法一：常规法

1.代码实现：


void QuickSort1(int* arr, int left, int right)
{
	int start = left, end = right, key = left;

	if (left >= right)
		return;

	while (left < right)
	{
		while (left < right && arr[right] >= arr[key])
			right--;
		while (left < right && arr[left] <= arr[key])
			left++;

		swap(&arr[left], &arr[right]);
	}

	swap(&arr[key], &arr[left]);

	key = left;

	QuickSort1(arr, start, key - 1);
	QuickSort1(arr, key + 1, end);
}

2.下面是单趟排序的逻辑：

2aa774f668f8497b97894ffcadca0e70.png

至于需要注意的点，就是当key在左侧时，一定要右侧先动，左侧再动，这样才能保证相遇点的值小于等于arr[key]（这个结论可以画图证明，这里就不展开了），当然，逆序同理。

3.下面是整体逻辑的详细解读，写代码时一定要注意细节，后续快排代码不再重复：

4978faa9cd9e4b35b23afafac2f5ef67.png

4.由于相遇点的值小于等于arr[key]这个结论一定程度上难以理解，于是就出现了一种优化方案——挖坑法，代码如下：


void QuickSort5(int* arr, int left, int right)
{
	if (left >= right)
		return;

	int start = left, end = right, key = left, piti = left;//存储坑的下标

	int tmp = arr[key];//用来初始坑里的值

	while (left < right)
	{
		while (left < right && arr[right] >= tmp)
			right--;

		if (left < right)
		{
			arr[piti] = arr[right];
			piti = right;
		}

		while (left < right && arr[left] <= tmp)
			left++;

		if (left < right)
		{
			arr[piti] = arr[left];
			piti = left;
		}
	}

	arr[piti] = tmp;

	key = piti;

	QuickSort5(arr, start, key - 1);
	QuickSort5(arr, key + 1, end);
}

5.当数组接近有序时，每次调用后key的位置都会很偏，导致递归次数接近N，总时间复杂度来到O(N ^ 2)，因此取key尤为关键，关键在于不要一来就取到最小值，因此随机取key和三数取中可以一定程度上缓解这个问题：，代码如下：

三数取中：


int GetMid(int* arr, int left, int right)
{
	int mid = (left + right) / 2;

	if (arr[mid] >= arr[left])
	{
		if (arr[mid] < arr[right])
			return mid;
		else
		{
			if (arr[left] < arr[right])
				return right;
			else
				return left;
		}
	}

	else
	{


		if (arr[mid] > arr[right])
			return mid;
		else
		{
			if (arr[right] < arr[left])
				return left;
			else
				return right;
		}
	}

}

随机取key：

int key = rand() % (right - left + 1) + left;//随机值

但是这些方法依旧不能完全消除快排的缺陷，当数组是1111111111这种时，时间复杂度依然会变成O(N ^ 2)

6.时间复杂度分析

快排的时间复杂度是O(NlogN)，分析方法如下：

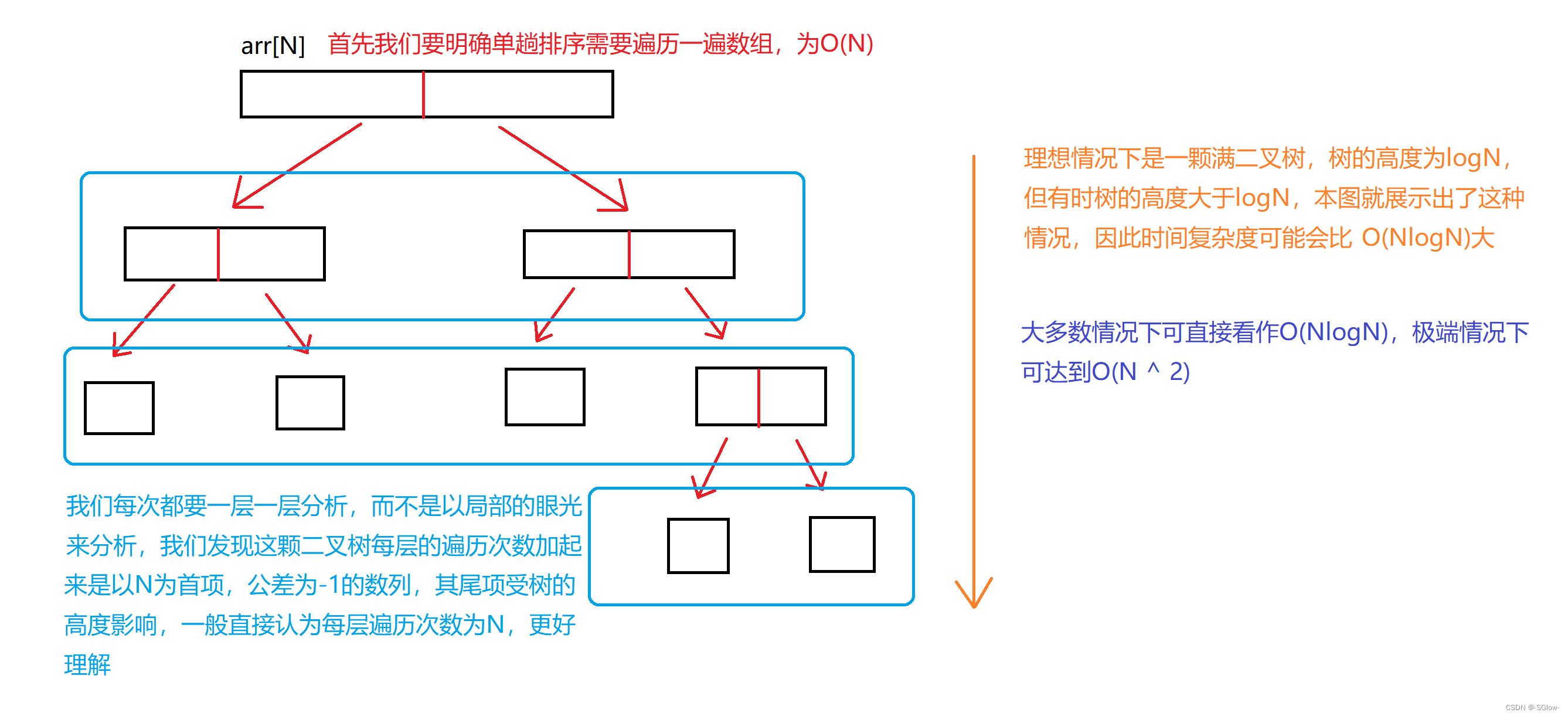
1abdf1502e1641ca8d215a2406310bbf.png

需要补充的是，logN与N的差别很大，N-logN依然是N的量级，举个例子：已知2的10次方是1024，假如有1024个数据，在快排中，单趟排序的遍历次数为1024、1023、1022一直到1014（末项可能会更小，但不会小多少），我们发现，这些数字差别很小，几乎是由N来决定的，所以上面图中说我们一般可以将单趟遍历的次数看作N

方法二：双指针法

这个方法的代码实现比较简单，关键在于prev指针和cur指针之间嵌入大于arr[key]的值，注意每次arr[prev]的下一个元素都是大于arr[key]的（当然也有可能相同或者没有元素，但是在这两种特殊情况下对我们功能的实现没有影响），最后交换arr[key]和arr[prev]达到一样的效果，使右侧大于arr[key]，左侧小于等于arr[key]。后续逻辑相同。

代码实现如下：


void QuickSort3(int* arr, int left, int right)
{
	int prev = left, cur = left + 1, key = left;

	if (left > right)
		return;

	while (cur <= right)
	{
		if (arr[cur] > arr[key])
			cur++;
		else
			swap(&arr[++prev], &arr[cur++]);
	}

	swap(&arr[key], &arr[prev]);

	key = prev;

	QuickSort3(arr, left, key - 1);
	QuickSort3(arr, key + 1, right);
}

方法三：非递归法

这种方法利用了前序遍历和栈的相似性。为什么说是前序遍历呢？因为在遍历时，该层遍历还同时保存了左递归和右递归的必要信息，就像二叉树的父节点能够找到子节点，而子节点找不到父节点。如果是中序或后序就没有这样的特性，就不适合用栈或队列等数据结构来实现。这也是为什么归并排序不适合用栈和队列来实现非递归。

代码如下：


void QuickSort4(int* arr, int left, int right)
{
	Stack s;
	StackInit(&s);
	StackPush(&s, right), StackPush(&s, left);//从右向左入栈

	while (!isStackEmpty(&s))
	{
		int left = StackTop(&s);
		StackPop(&s);
		int right = StackTop(&s);
		StackPop(&s);

		int prev = left, cur = left + 1, key = left;//从左向右取数据

		while (cur <= right)
		{
			if (arr[cur] > arr[key])
				cur++;
			else
				swap(&arr[++prev], &arr[cur++]);
		}

		swap(&arr[key], &arr[prev]);

		key = prev;

		if(key + 1 < right)
			StackPush(&s, right), StackPush(&s, key + 1);//后取得
		if(left < key - 1)
			StackPush(&s, key - 1), StackPush(&s, left);//先取得

	}

	StackDestroy(&s);
}

相关栈的功能实现如下：


void StackInit(Stack* ps)
{
	ps->arr = NULL;
	ps->capacity = ps->size = 0;
}

void StackPush(Stack* ps, int val)
{
	if (ps->capacity == ps->size)
	{
		ps->capacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		int* tmp = (int*)realloc(ps->arr, sizeof(int) * ps->capacity);
		assert(tmp);
		ps->arr = tmp;
	}

	ps->arr[ps->size++] = val;
}

int StackTop(Stack* ps)
{
	return ps->arr[ps->size - 1];
}

void StackPop(Stack* ps)
{
	ps->size--;
}

bool isStackEmpty(Stack* ps)
{
	return ps->size == 0;
}

void StackDestroy(Stack* ps)
{
	free(ps->arr), ps->arr = NULL;
	ps->capacity = ps->size = 0;

}

需要注意入栈顺序是从右向左，右下标先入，左下标后入，右递归先入，左递归后入。基本逻辑和递归相似，理解了原理就很好写。

二、归并排序

归并排序一定程度上比较好理解，但非递归法需要注意的细节比较多

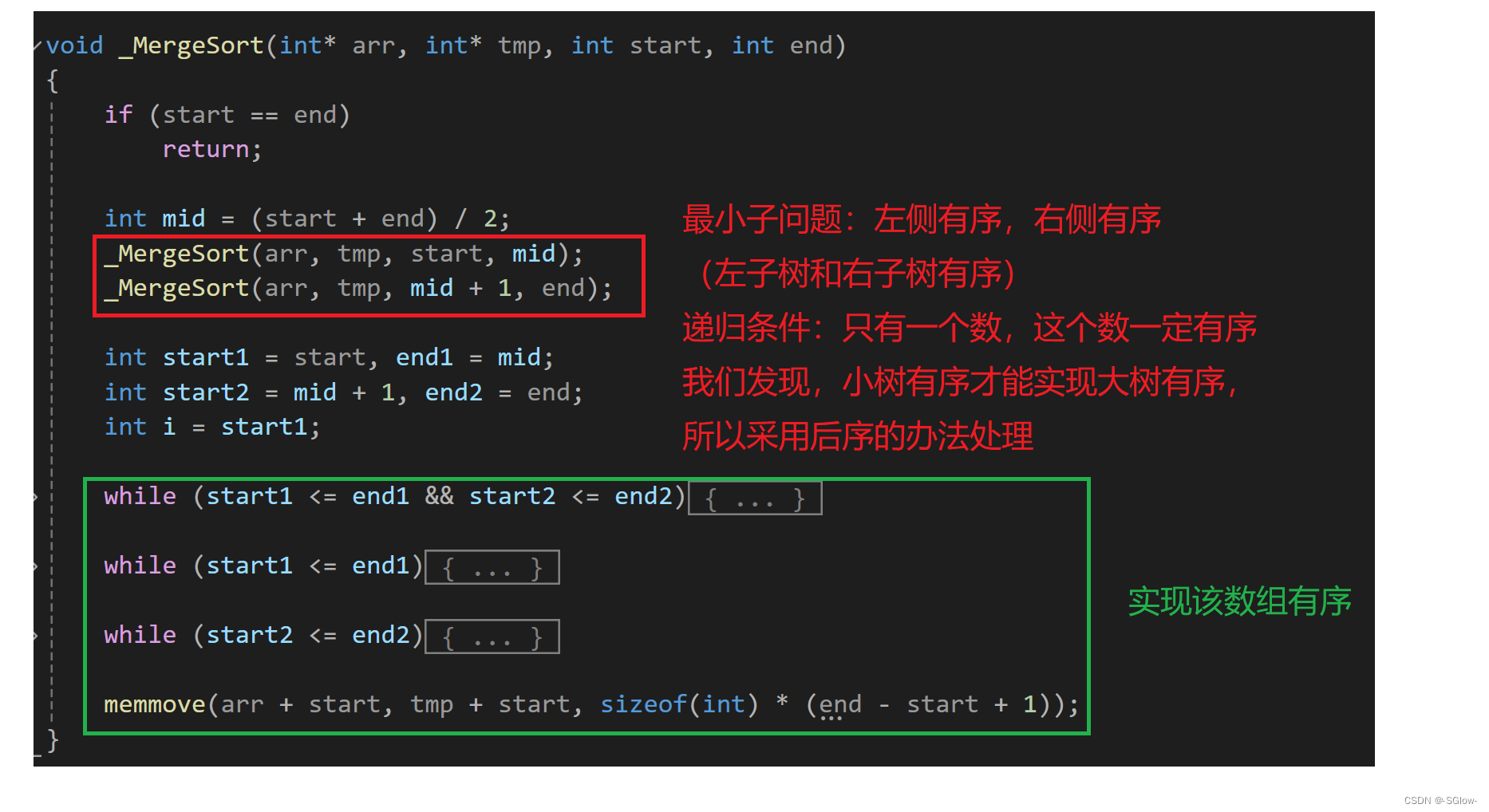
方法一：递归法


void _MergeSort(int* arr, int* tmp, int start, int end)
{
	if (start == end)
		return;

	int mid = (start + end) / 2;
	_MergeSort(arr, tmp, start, mid);
	_MergeSort(arr, tmp, mid + 1, end);

	int start1 = start, end1 = mid;
	int start2 = mid + 1, end2 = end;
	int i = start1;

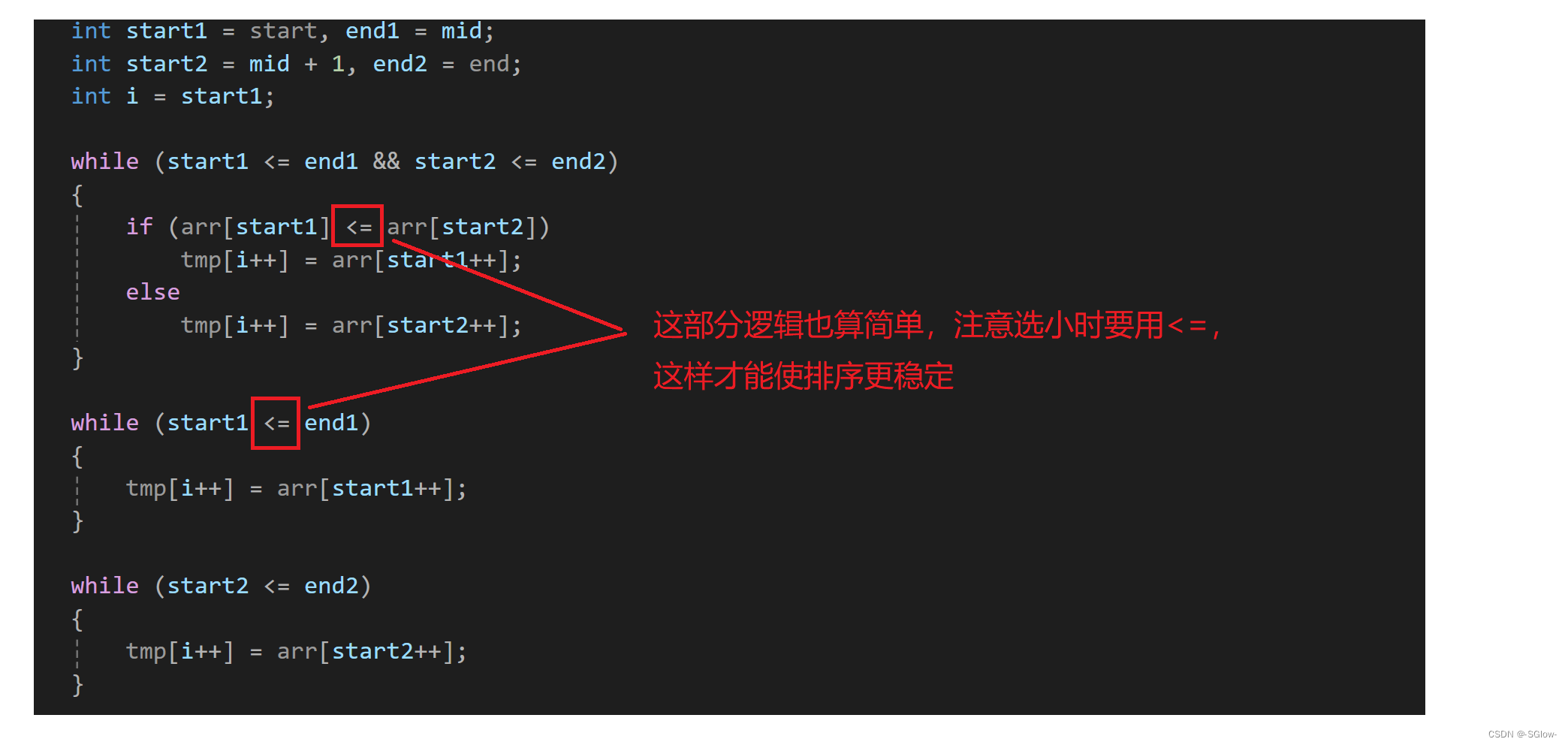
	while (start1 <= end1 && start2 <= end2)
	{
		if (arr[start1] <= arr[start2])
			tmp[i++] = arr[start1++];
		else
			tmp[i++] = arr[start2++];
	}
	
	while (start1 <= end1)
	{
		tmp[i++] = arr[start1++];
	}

	while (start2 <= end2)
	{
		tmp[i++] = arr[start2++];
	}

	memmove(arr + start, tmp + start, sizeof(int) * (end - start + 1));
}


void MergeSort1(int* arr, int size)
{
	int* tmp = (int*)malloc(sizeof(int) * size);
	assert(tmp);

	_MergeSort(arr, tmp, 0, size - 1);

	free(tmp), tmp = NULL;
}

整体逻辑：

0de86724086243989b9150329223f24f.png

7e75af49074e4b4b87edbf835f8b5a28.png

方法二：非递归法

非递归法理解起来较为困难，下面详细分析：

代码实现：


void MergeSort2(int* arr, int size)
{
	int* tmp = (int*)malloc(sizeof(int) * size);
	assert(tmp);

	int gap = 1;

	while (gap <= size)
	{

		for (int i = 0; i < size; i += 2 * gap)
		{
			int start1 = i, end1 = start1 + gap - 1;
			int start2 = end1 + 1, end2 = start2 + gap - 1;
			int j = start1;

			if (end1 >= size || start2 >= size)
				break;
			while (end2 >= size)
				end2--;

			while (start1 <= end1 && start2 <= end2)
			{
				if (arr[start1] <= arr[start2])
					tmp[j++] = arr[start1++];
				else
					tmp[j++] = arr[start2++];
			}

			while (start1 <= end1)
			{
				tmp[j++] = arr[start1++];
			}

			while (start2 <= end2)
			{
				tmp[j++] = arr[start2++];
			}

			memmove(arr + i, tmp + i, sizeof(int) * (end2 - i + 1));

		}

		gap *= 2;
	}

	free(tmp), tmp = NULL;
}

1.整体逻辑

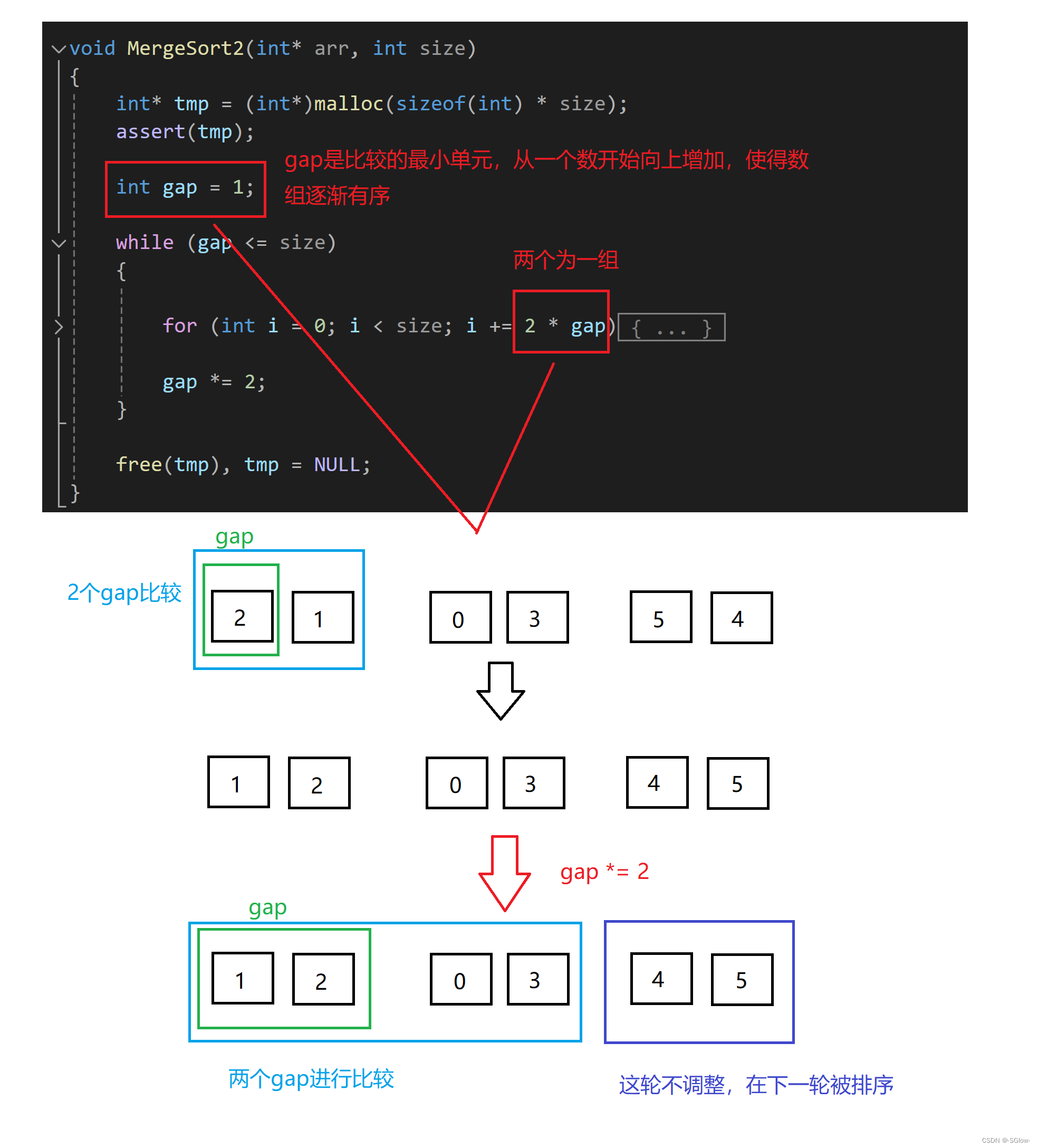
ace813579db94594a8961f1fb9b515d1.png

它的逻辑大体上和递归法相似，但非递归法是直接从最小元素开始向上归并。

2.非递归归并的难点在于数组前面归并是两两为一组，会导致有落单的情况，需要进行处理，上面这张图就展示出了一种情况，下面分析一下：

90cef48aca034af8b525250f38bf479d.png

三、计数排序

这个排序非常简单，不做过多分析

代码实现：


void CountSort(int* arr, int size)
{
	int max = arr[0], min = arr[0];

	for (int i = 0; i < size; i++)
	{
		if (arr[i] > max)
			max = arr[i];
		if (arr[i] < min)
			min = arr[i];
	}

	int range = max - min + 1;

	int* count = (int*)calloc(range, sizeof(int));
	assert(count);

	for (int i = 0; i < size; i++)
	{
		count[arr[i] - min]++;
	}

	for (int i = 0, j = 0; i < range; i++)
	{
		while (count[i]--)
		{
			arr[j++] = i + min;
		}
	}

}

注意这个方法用于数据集中时使用，这个时候效率很高。但分散数据就别用，会浪费大量空间。这个排序讨论其稳定性没有意义，因为它只能做到数值的排序，这些排序后没有意义。

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1560654.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

详细分析Mysql中的STR_TO_DATE基本知识（全）

详细分析Mysql中的STR_TO_DATE基本知识（全）

目录 前言1. 基本知识2. Demo3. 实战Demo4. Sql彩蛋4.1 LPAD函数4.2 SUBSTRING_INDEX函数 5. Java彩蛋 前言 对于该知识点&#xff0c;主要因为数据库类型为String&#xff08;类似2024-03-26&#xff09;&#xff0c;放置于后端操作后&#xff0c;需要自定义比较&#xff0c;…
阅读更多...
LLaMA-Factory微调（sft）ChatGLM3-6B保姆教程

LLaMA-Factory微调（sft）ChatGLM3-6B保姆教程

LLaMA-Factory微调&#xff08;sft&#xff09;ChatGLM3-6B保姆教程 准备 1、下载 下载LLaMA-Factory下载ChatGLM3-6B下载ChatGLM3windows下载CUDA ToolKit 12.1 &#xff08;本人是在windows进行训练的&#xff0c;显卡GTX 1660 Ti&#xff09; CUDA安装完毕后&#xff0c…
阅读更多...
HCIP---MGRE和GRE实验

HCIP---MGRE和GRE实验

一、配置ip R1: [R1]int g0/0/0 [R1-GigabitEthernet0/0/0]ip add 192.168.1.254 24 [R1-GigabitEthernet0/0/0]int s4/0/0 [R1-Serial4/0/0]ip add 15.1.1.1 24 [R1]ip route-static 0.0.0.0 0 15.1.1.5 R2: [R2]int g0/0/0 [R2-GigabitEthernet0/0/0]ip add 192.168.2.2…
阅读更多...
GROBID库文献解析

GROBID库文献解析

1. 起因 由于某些原因需要在大量的文献中查找相关内容&#xff0c;手动实在是太慢了&#xff0c;所以选择了GROBID库进行文献批量解析 2. GROBID介绍 GROBID是一个机器学习库&#xff0c;用于将PDF等原始文档提取、解析和re-structuring为结构化的XML/TEI编码文档&#xff0…
阅读更多...
C++第十四弹---模板初阶

C++第十四弹---模板初阶

✨个人主页&#xff1a; 熬夜学编程的小林 &#x1f497;系列专栏&#xff1a; 【C语言详解】 【数据结构详解】【C详解】 目录 1、泛型编程 2、函数模板 2.1、函数模板的概念 2.2、函数模板的格式 2.3、函数模板的原理 2.4、函数模板的实例化 2.5、模板参数的匹配原则 …
阅读更多...
【学习】如何成为资深的软件测试工程师“大神”？

【学习】如何成为资深的软件测试工程师“大神”？

一个优秀的软件测试工程师不仅需要有深厚的技术知识和经验&#xff0c;还需要有良好的沟通能力、分析能力和问题解决能力。总的来说&#xff0c;一个"大神"一样的软件测试工程师应该是一个全面的技术专家&#xff0c;同时还需要有出色的沟通和问题解决能力&#xff0…
阅读更多...
Mac 版 IDEA 中配置 GitLab

Mac 版 IDEA 中配置 GitLab

一、安装Git 在mac终端输入Git检测指令&#xff0c;可以通过git命令查看Git是否安装过&#xff0c;如果没有则会弹出安装按钮&#xff0c;如果安装过则会输出如下信息。 WMBdeMacBook-Pro:~ WENBO$ git usage: git [--version] [--help] [-C <path>] [-c namevalue][--…
阅读更多...
ubuntu23.10配置RUST开发环境

ubuntu23.10配置RUST开发环境

系统版本: gcc版本 下载rustup安装脚本: curl --proto https --tlsv1.2 https://sh.rustup.rs -sSf | sh下载完成后会自动执行 选择默认安装选项 添加cargo安装目录到环境变量 vim ~/.bashrc 默认已添加 使用环境变量立即生效 source ~/.bashrc 执行rust开发环境,在终端输入…
阅读更多...
深度剖析：计算机集群在大数据体系中的关键角色和技术要点

深度剖析：计算机集群在大数据体系中的关键角色和技术要点

什么是计算机集群&#xff1f; 计算机集群是一组相互连接的计算机&#xff08;服务器&#xff09;&#xff0c;它们协同工作以完成共同的任务。集群中的每个计算机节点都可以独立运行&#xff0c;但它们通过网络连接在一起&#xff0c;以实现更高的可靠性、性能和可扩展性。 典…
阅读更多...
给虚拟机配置静态IP并使用FileZIlla在虚拟机和Windows之间传输文件（ssh和ftp两种方法）

给虚拟机配置静态IP并使用FileZIlla在虚拟机和Windows之间传输文件（ssh和ftp两种方法）

一、配置操作系统网络 &#x1f338;下面的步骤主要是配置虚拟机的静态IP&#xff0c;方便后续用 FikeZilla 在windows和虚拟机之间传输文件&#xff08;否则用默认的ip分配方案为 DHCP ,每一次开机时的ip都是有可能不同的,这样就会导致每次远程连接都需要查看ip地址.&#xf…
阅读更多...
Python | 非规则矩形投影添加斑马线边框

Python | 非规则矩形投影添加斑马线边框

前言 在地图绘制领域&#xff0c;非规则投影的示例相对较少&#xff0c;通过几个python的示例可以更好地理解如何在不同投影类型和边界形状下绘制地图。 以下提供了一系列示例&#xff0c;演示了如何在地图中添加非规则边界和边框。这些示例涵盖了不同的投影类型和边界形状&a…
阅读更多...
element-ui 表单校验，失去焦点/框内值改变，校验

element-ui 表单校验，失去焦点/框内值改变，校验

前提&#xff1a;在el-form表单中&#xff0c;框中有值&#xff0c;失去焦点或者框内值改变的时候&#xff0c;校验提示&#xff0c;依旧没有消失el-select校验失效问题 之前el-select&#xff0c;trigger时候用的“blur”,导致失效&#xff0c;现在 el-select 统一改为"c…
阅读更多...
PyTorch深度学习实战（40）——零样本学习(Zero-Shot Learning)

PyTorch深度学习实战（40）——零样本学习(Zero-Shot Learning)

PyTorch深度学习实战&#xff08;40&#xff09;——零样本学习 0. 前言1. 零样本学习2. 实现零样本学习模型2.1 模型分析2.2 构建零样本学习模型 小结系列链接 0. 前言 零样本学习 (Zero-Shot Learning) 是一种机器学习方法&#xff0c;旨在解决传统监督学习中&#xff0c;当…
阅读更多...
pulsar存在大量消费未ack的原因

pulsar存在大量消费未ack的原因

问题起源&#xff1a; 某产品灰度上线后&#xff0c;从pulsar服务端监控发现存在一种现象&#xff1a;消费但未ack的信息不断增加&#xff0c;直到3000左右就稳定下来了且消费速度为0&#xff0c;但不清楚这3000是怎么来的&#xff0c;因为代码是消费到立马ack的&#xff1b; …
阅读更多...
格雷希尔G10系列L150A和L200A气动快速连接器，在新能源汽车线束线缆剥线后的气密性测试密封方案

格雷希尔G10系列L150A和L200A气动快速连接器，在新能源汽车线束线缆剥线后的气密性测试密封方案

线束线缆在很多用电环境都有使用&#xff0c;比如说新能源汽车&#xff0c;从电池包放电开始&#xff0c;高低压、通讯都开始进行工作&#xff0c;线束在连接的地方需要具有较高的气密性和稳定性&#xff0c;才能保证车辆在不同环境下能够正常的运行。 线束在组装铜鼻子前需要剥…
阅读更多...
【Oracle篇】expdp/impdp高效完成全部生产用户的全库迁移（第四篇，总共四篇）

【Oracle篇】expdp/impdp高效完成全部生产用户的全库迁移（第四篇，总共四篇）

☘️博主介绍☘️&#xff1a; ✨又是一天没白过&#xff0c;我是奈斯&#xff0c;DBA一名✨ ✌✌️擅长Oracle、MySQL、SQLserver、Linux&#xff0c;也在扩展大数据方向的知识面✌✌️ ❣️❣️❣️大佬们都喜欢静静的看文章&#xff0c;并且也会默默的点赞收藏加关注❣️❣️…
阅读更多...
基于SpringBoot的游戏商城系统的设计与实现(论文+源码)_kaic

基于SpringBoot的游戏商城系统的设计与实现(论文+源码)_kaic

目录 1前言 1.1研究的背景及意义 1.2国内外的研究状况和发展趋势 2需求分析 2.1系统需求分析 2.1.1技术可行性 2.1.2经济可行性 2.1.3操作可行性 2.2系统的开发环境 2.2.1 Springboot框架 2.2.2 数据库Mysql 2.2.3 IntelliJ IDEA平台 2.2.4 Mybatis和MyBatis-plus 2.2.5 前端框…
阅读更多...
火鸟门户同城模块

火鸟门户同城模块

同城活动 同城活动是指在同一城市举办的活动&#xff0c;可以是多种类型&#xff0c;例如&#xff1a; 聚会&#xff1a;朋友聚会、同学聚会、兴趣爱好聚会等。展览&#xff1a;艺术​​展览、科技展览、文化展览等。演出节目&#xff1a;演唱会、音乐会、戏剧表演等。比赛项…
阅读更多...
JumpServer 堡垒主机

JumpServer 堡垒主机

JumpServer 堡垒机帮助企业以更安全的方式管控和登陆各种类型的资产 SSH&#xff1a;Linux/Unix/网络设备等Windows&#xff1a;Web方式连接/原生RDP连接数据库&#xff1a;MySQL、Oracle、SQLServer、PostgreSQL等Kubernetes&#xff1a;连接到K8s集群中的PodsWeb站点&#x…
阅读更多...
Backend - gitea 首次建库（远端本地）

Backend - gitea 首次建库（远端本地）

目录 一、建立远端储存库 1. 进入新增画面 2. 填写储存库名称&#xff08;如book&#xff09;&#xff0c;点击“建立”即可 二、本地关联远端储存库 1. 本地初始化储存库代码 &#xff08;1&#xff09;新建文件夹 &#xff08;2&#xff09;获取远端储存库 2. 本地编写…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023