目录
1.排序的概念及其运用
1.1排序的概念
1.2排序运用
1.3常见的排序算法
2.插入排序
2.1 原理演示:编辑
2.2 算法实现
2.3 算法的时间复杂度和空间复杂度分析
3.希尔排序
3.1算法思想
3.2原理演示
3.3代码实现
3.4希尔算法的时间复杂度
4.冒泡排序
4.1冒泡排序原理(图解)
4.2.冒泡排序实现
4.3冒泡排序封装为函数
4.4 冒泡排序代码效率改进。
5.堆排序
5.1升序建大堆,降序建小堆
5.2 建堆的时间复杂度
5.2.1 向下调整建堆
5.2.2向上调整建堆
5.3 排序实现
6.选择排序
6.1基本思想:
6.2算法演示
6.3代码实现
6.4时间复杂度分析
7.快速排序
7.1 hoare版本
7.1.1算法图解
7.1.2代码实现
7.1.3 算法优化---三数取中
7.2挖坑法快排
7.2.1算法图解
7.2.2 代码实现
7.3 前后指针法
7.4快速排序进一步优化
7.5快速排序非递归写法
8.归并排序
9.计数排序
10.结语
深度优先遍历 dfs : 先往深处走,走到没有了再往回,前序遍历 一般是递归
广度优先遍历 bfs 层序遍历 一般用队列
1.排序的概念及其运用
1.1排序的概念
1.2排序运用
1.3常见的排序算法

2.插入排序
算法思想:
和我们玩扑克牌整理牌的时候是非常相像的

将我们的摸到的牌作为手里的牌的最后一张,从倒数第一张开始到第一张逐次比较,如果当前牌大于前一张就放置在当前位置,如果小于那就向前移动,最坏的情况就是每次摸到牌都要逐渐比较放到最前面。
2.1 原理演示: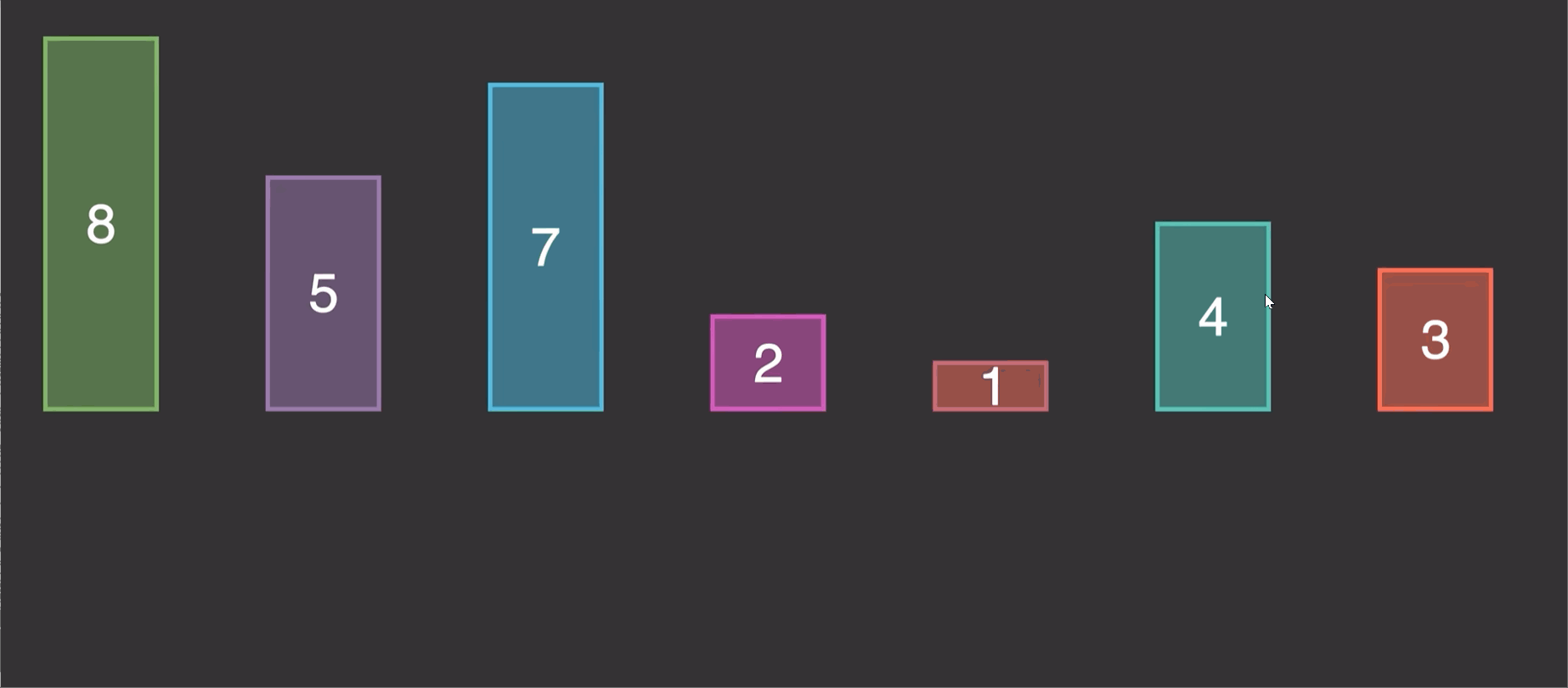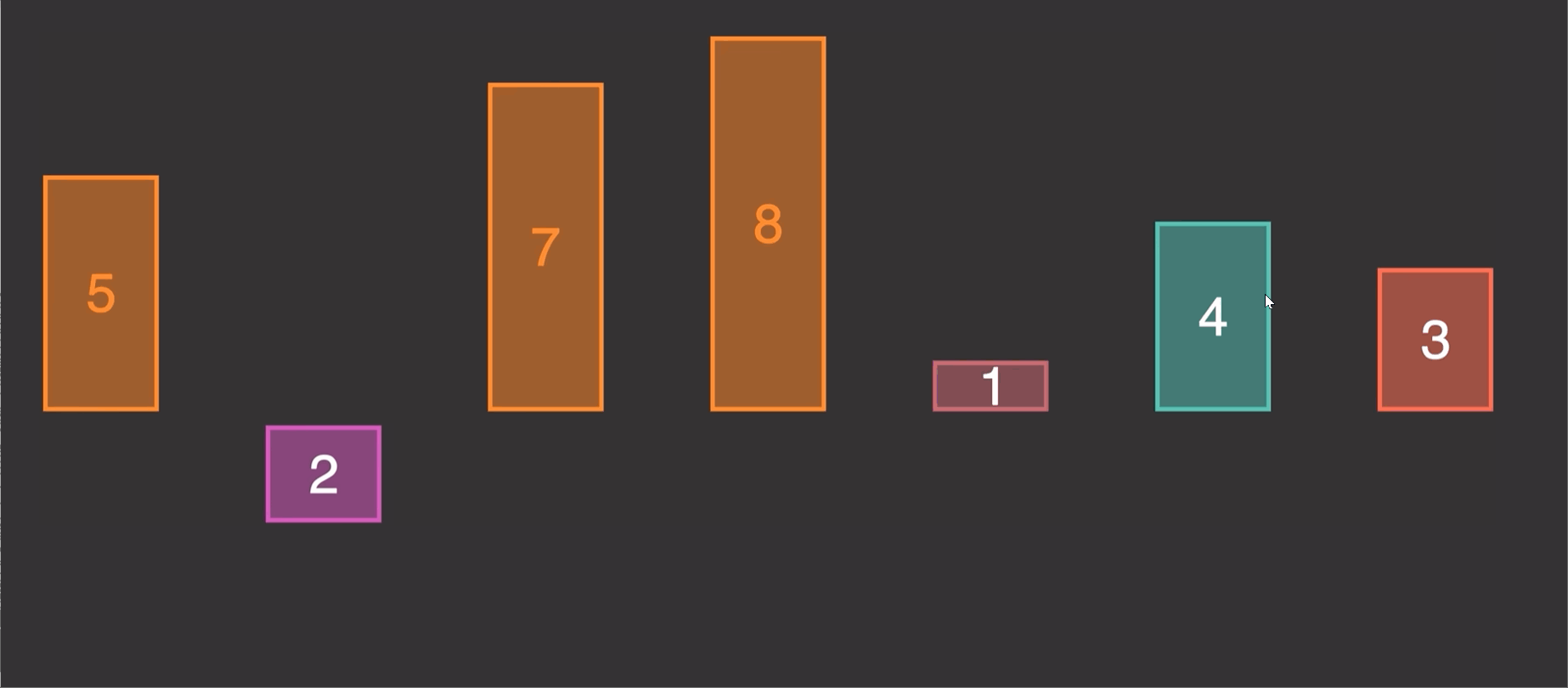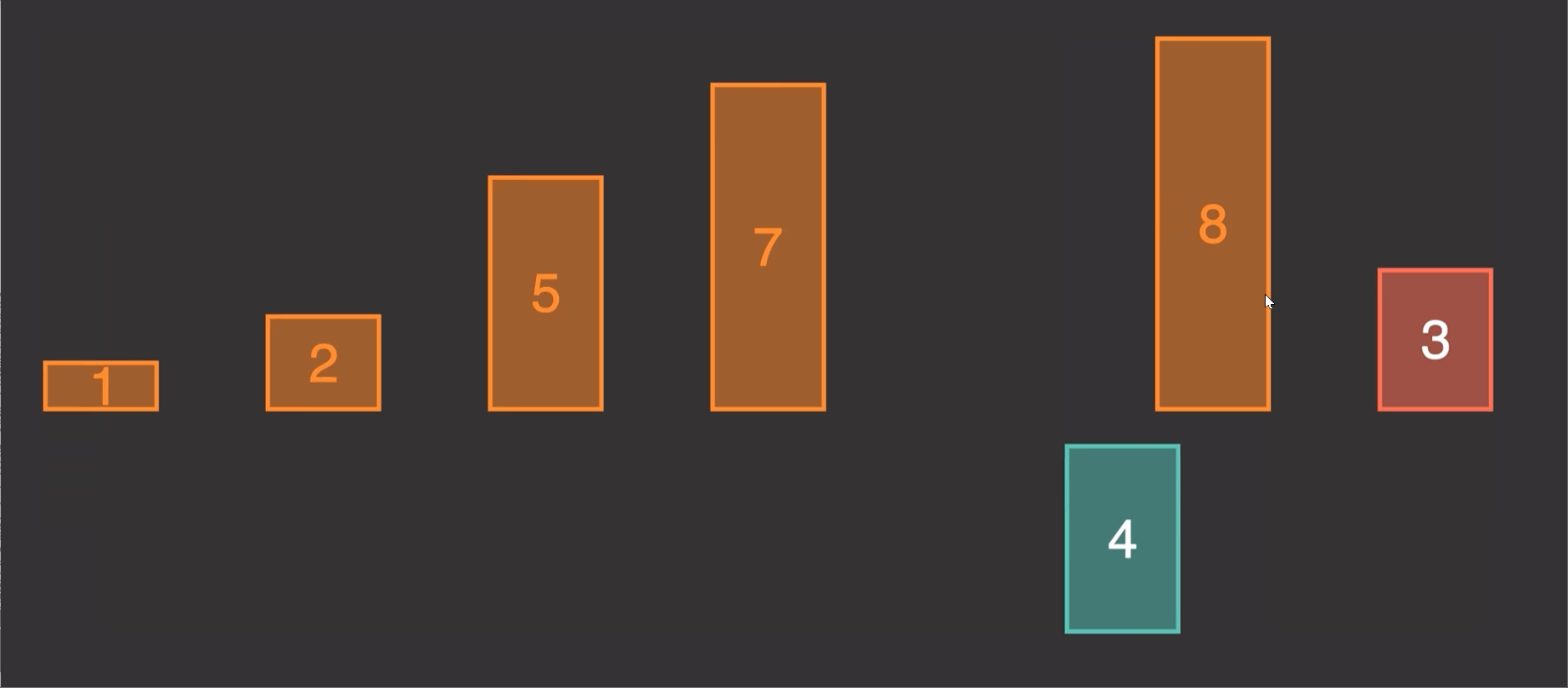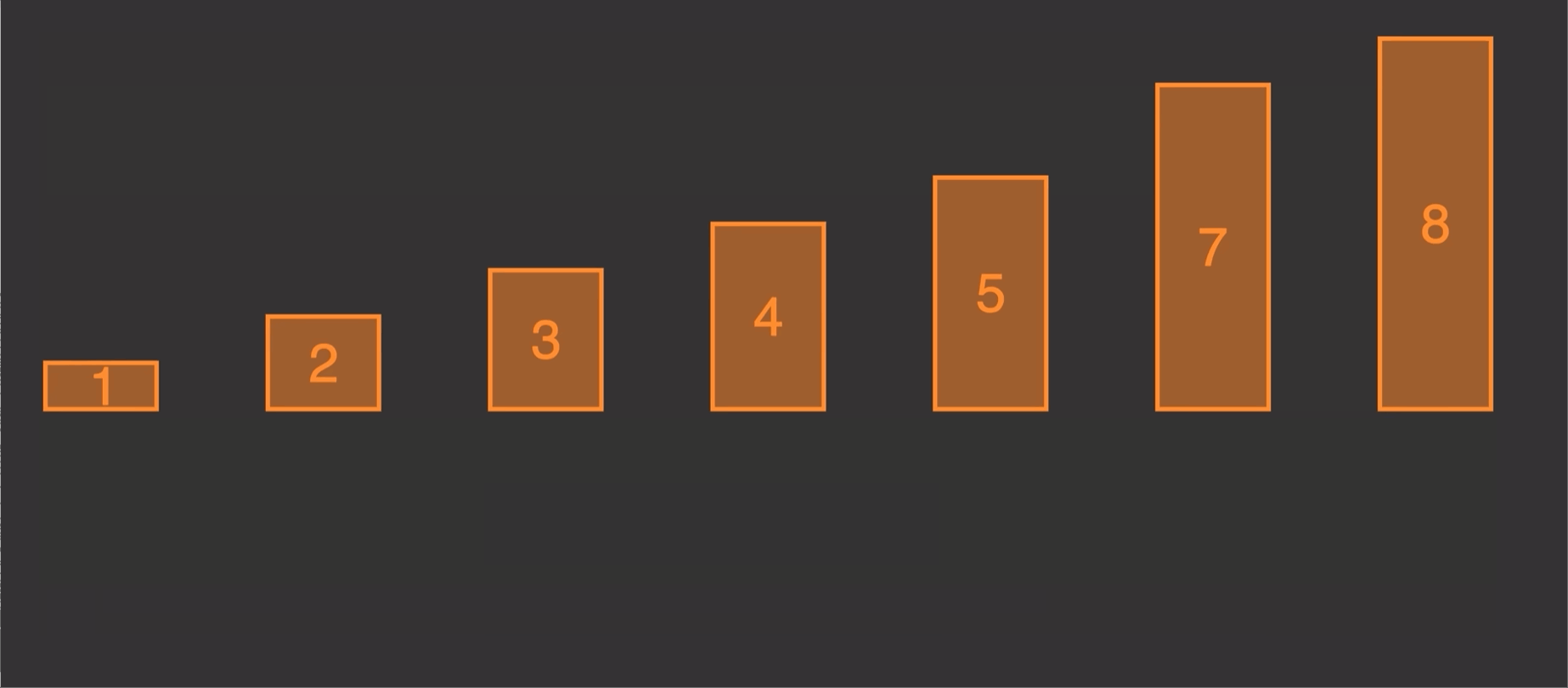
2.2 算法实现
由原理图我们知道这个算法的实现就是第二个先和1第一个比较,调整位置,第三个又和前两个进行比较调整位置。
第一次 调整前两个位置
第二次 调整前三个位置
第三次 调整前四个位置
。。。
n个元素,就调整n-1次
每一次调整,都是倒数一个与倒数第二个比较调整完,倒数第二个又和倒数第三个做比较,知道比较到倒数最后一个也就是最开始的一个。
void InserPort(int* a, int n)
{
int i = 0;
for (i = 0; i < n - 1; i++)//n个元素调整n-1次
{
int end = i;
int tmp = a[end + 1];//最后一个元素值给tmp
while (end >= 0)
{
if (tmp < a[end])
{
//交换
a[end + 1] = a[end];
a[end] = tmp;
}
else
{
//不动
break;
}
//继续比较调整前两个
end--;
}
}
}
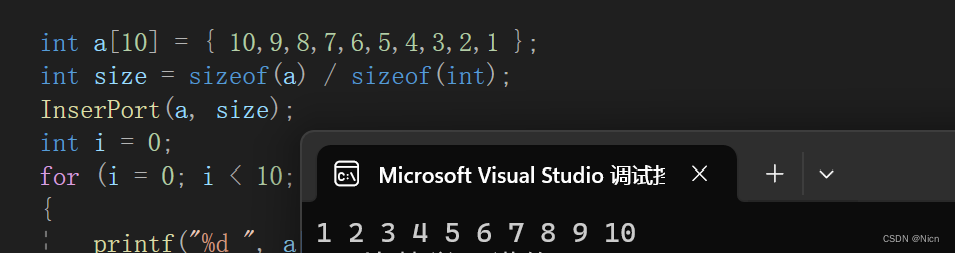
2.3 算法的时间复杂度和空间复杂度分析
上述代码就是最坏的情况:

时间复杂度为O(N^2)
空间复杂度为O(1)
3.希尔排序
3.1算法思想
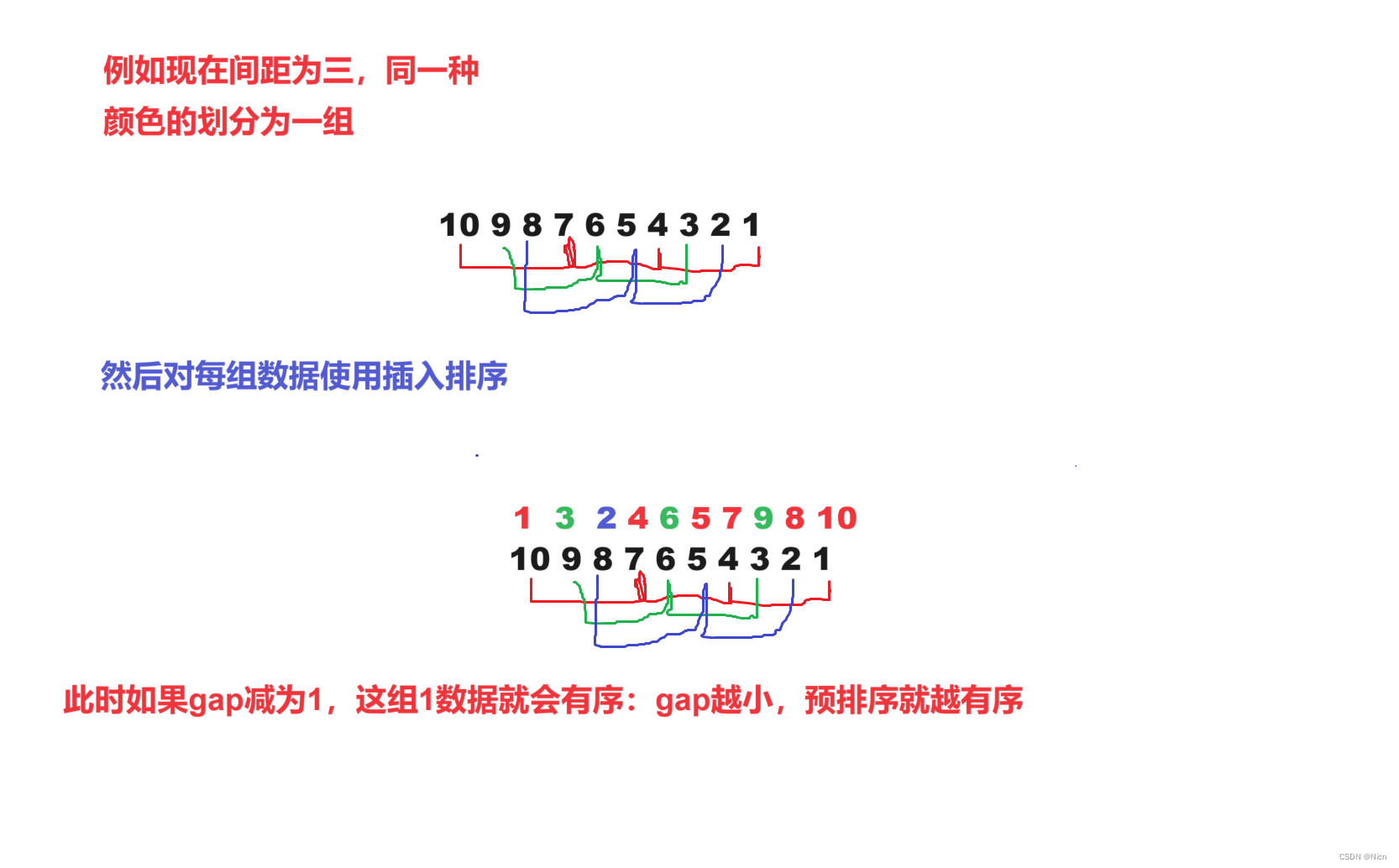
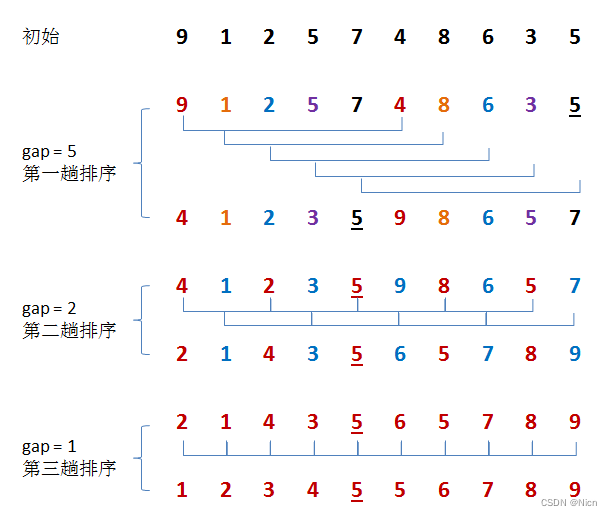
3.2原理演示
3.3代码实现
ShellSort(int* a, int n)
{
int i = 0;
int gap = n;
while (gap > 1)
{
gap /= 2;
for (i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end>gap)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
a[end] = tmp;
}
else
{
break;
}
end -= gap;
}
}
}
}3.4希尔算法的时间复杂度

《数据结构》--严蔚敏
 《数据结构-用面相对象方法与C++描述》--- 殷人昆
《数据结构-用面相对象方法与C++描述》--- 殷人昆
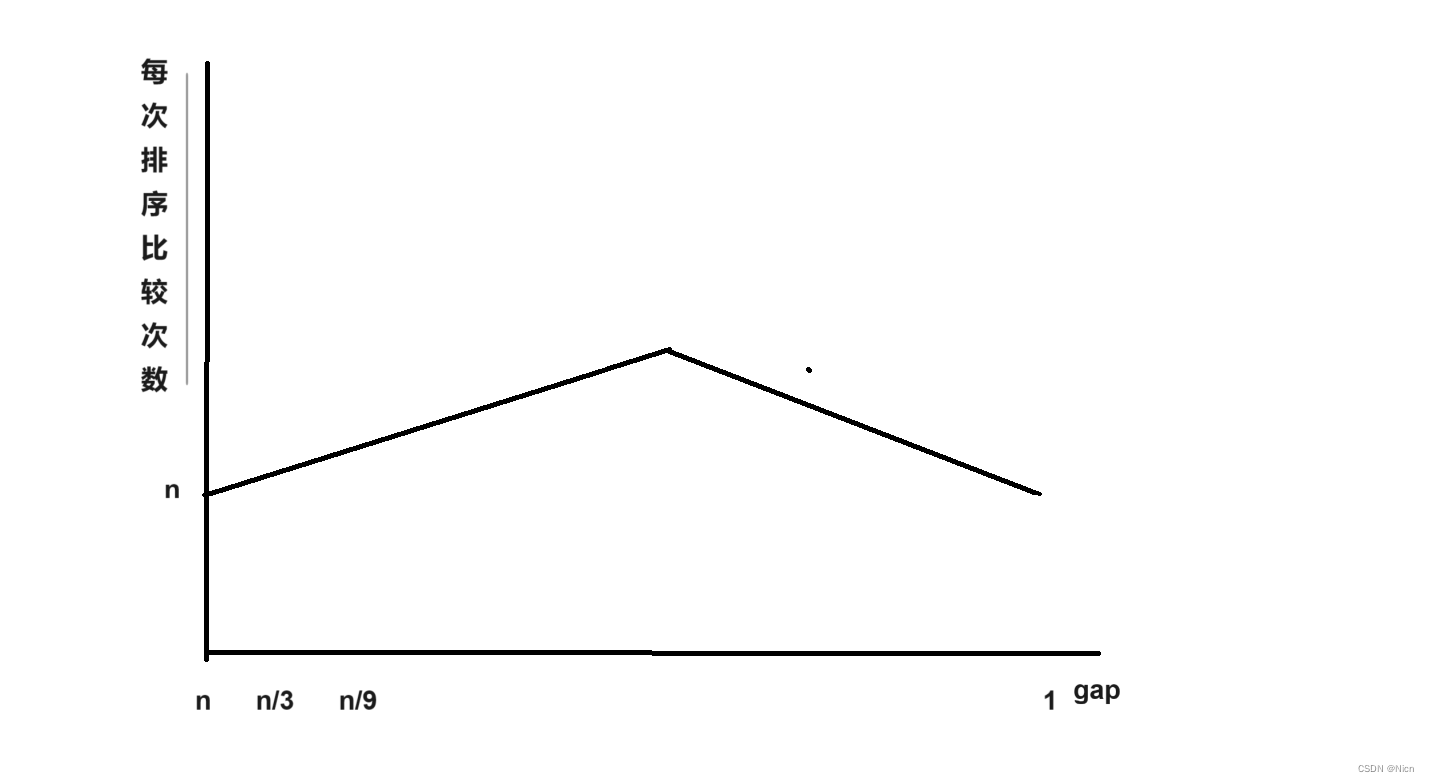
按照: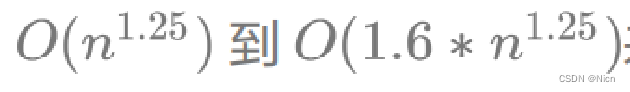
来计算
空间复杂度为O(1)
稳定性:不稳定
4.冒泡排序
核心思想:两两相邻的元素相比较是一种交换排序
4.1冒泡排序原理(图解)

4.2.冒泡排序实现
通过图解原理我们可以发现规律(以10个元素排列举例)
1.每一趟比较完全完成就把这一趟数据的最大数放在最后,第一趟是10个数据中的最大值9在最后,第二趟是9个数据中的8在最后,那么我们10个元素就要循环9趟,那么n个数据,就要循环n - 1趟。
2.第一趟是10个数据,就有9对数据比较,那么第二趟,就有8对数据进行比较。如果一趟有n个数据就要比较n - 1对数据。
3.所以需要两层循环,外层控制趟数,内层控制每一趟要比较的次数。
看如下实现。
int main()
{
int len[10] = { 0 };
int i = 0;
for (i = 0; i < 10; i++)
{
scanf("%d",&len[i]);
}
int n = sizeof(len) / sizeof(len[0]);
//printf("%d", n);
int x = 0;
for (x = 0; x < n; x++)
{
int y = 0;
{
for (y = 0; y < n-1 - x; y++)
{
if (len[y] > len[y + 1])
{
int temp = 0;
temp = len[y];
len[y] = len[y + 1];
len[y + 1] = temp;//交换
}
}
}
}
int j = 0;
for (j = 0; j < 10; j++)
{
printf(" %d ", len[j]);
}
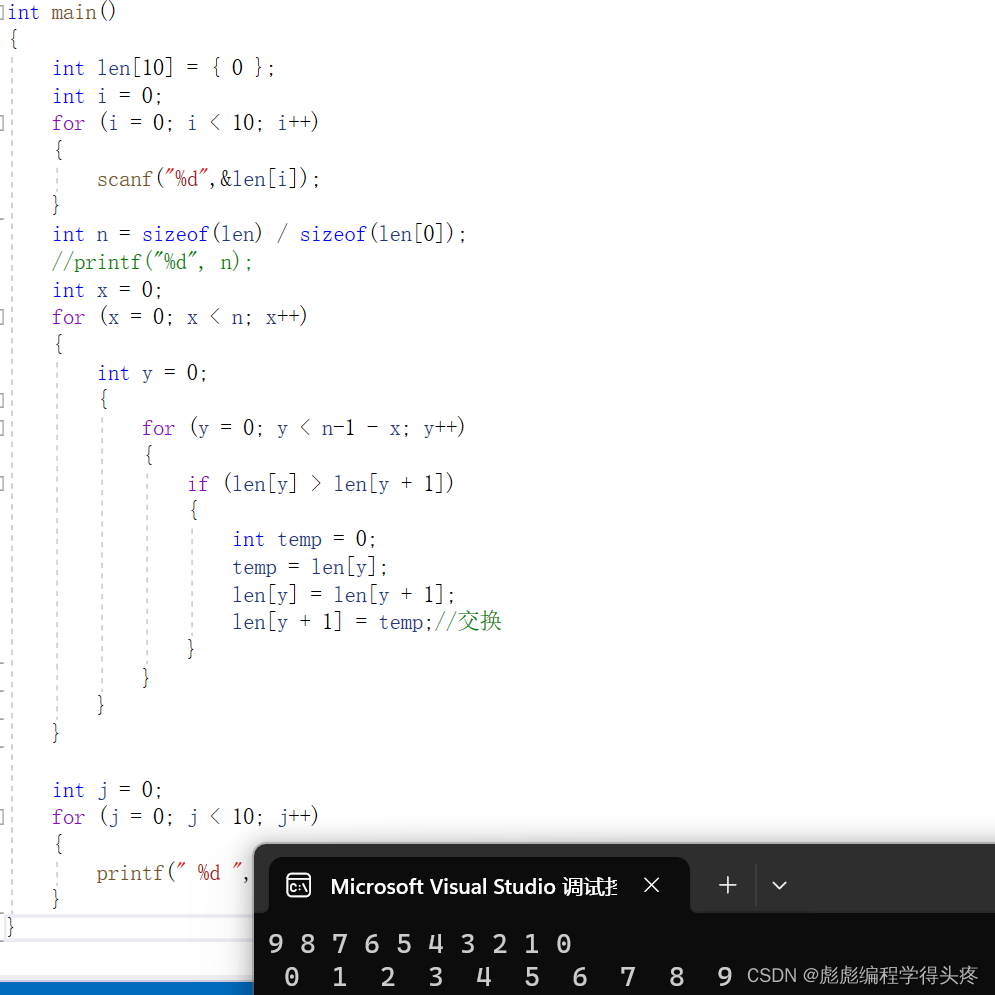
}运行结果如图,大家也可以用源码自己体验一下效果:
4.3冒泡排序封装为函数
现在已经实现了冒泡排序,为了以后的方便,我们来试着将这个冒泡排序模块功能封装为一个函数。让我们一起来看看自定义为函数有那些坑。
按照上述排序规则和封装函数的方法,我们将数组作为一个函数参数,传递给冒泡排序函数来执行冒泡排序,我们来看一下:
void BBurd_sort(int arr[10])
{
int n= sizeof(arr) / sizeof(arr[0]);
int x = 0;
for (x = 0; x < n; x++)
{
int y = 0;
{
for (y = 0; y < n - 1 - x; y++)
{
if (arr[y] > arr[y + 1])
{
int temp = 0;
temp = arr[y];
arr[y] = arr[y + 1];
arr[y + 1] = temp;//交换
}
}
}
}
}
int main()
{
int arr[10] = { 0 };
int i = 0;
for (i = 0; i < 10; i++)
{
scanf("%d", &arr[i]);
}
//int sz = sizeof(arr) / sizeof(arr[0]);
BBurd_sort(arr);
int j = 0;
for (j = 0; j < 10; j++)
{
printf(" %d ", arr[j]);
}
return 0;
}
我们观察到没有发生排序,我们调试看一下:
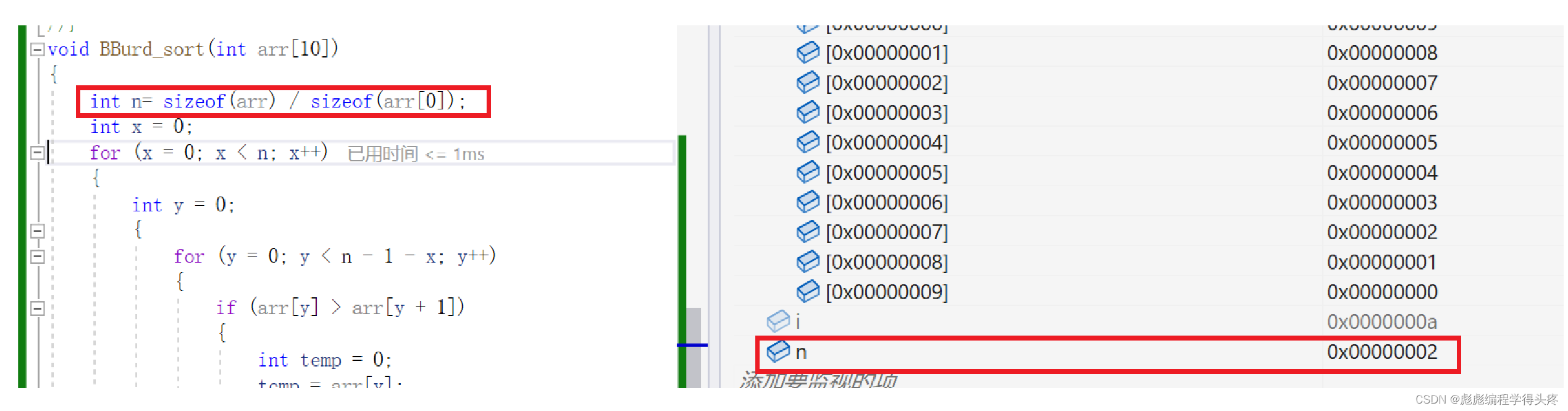
问题所在:我们这里想要实现的功能是n 保存的是数组的大小,那么应该是10才对,为什么是2呢。
思考:sizeof(arr[0] 求的是一个整形数组元素的大小那么其大小就应该是4字节,
那么说明我们的sizeof(arr)就是8字节,那么只有可能我们这里的arr,并不是一整个数组,而是一个地址 (地址也就是指针,在32位操作系统下面大小是4个字节,64位操作系统下是8个字节),那就说明我们这里的arr实质上是一个指针,保存的是数组首元素的地址。
所以在函数里面是没有办法求出这个数组的大小,解决办法,把函数的大小作为一个函数的参数一起传递,看一下改进效果。
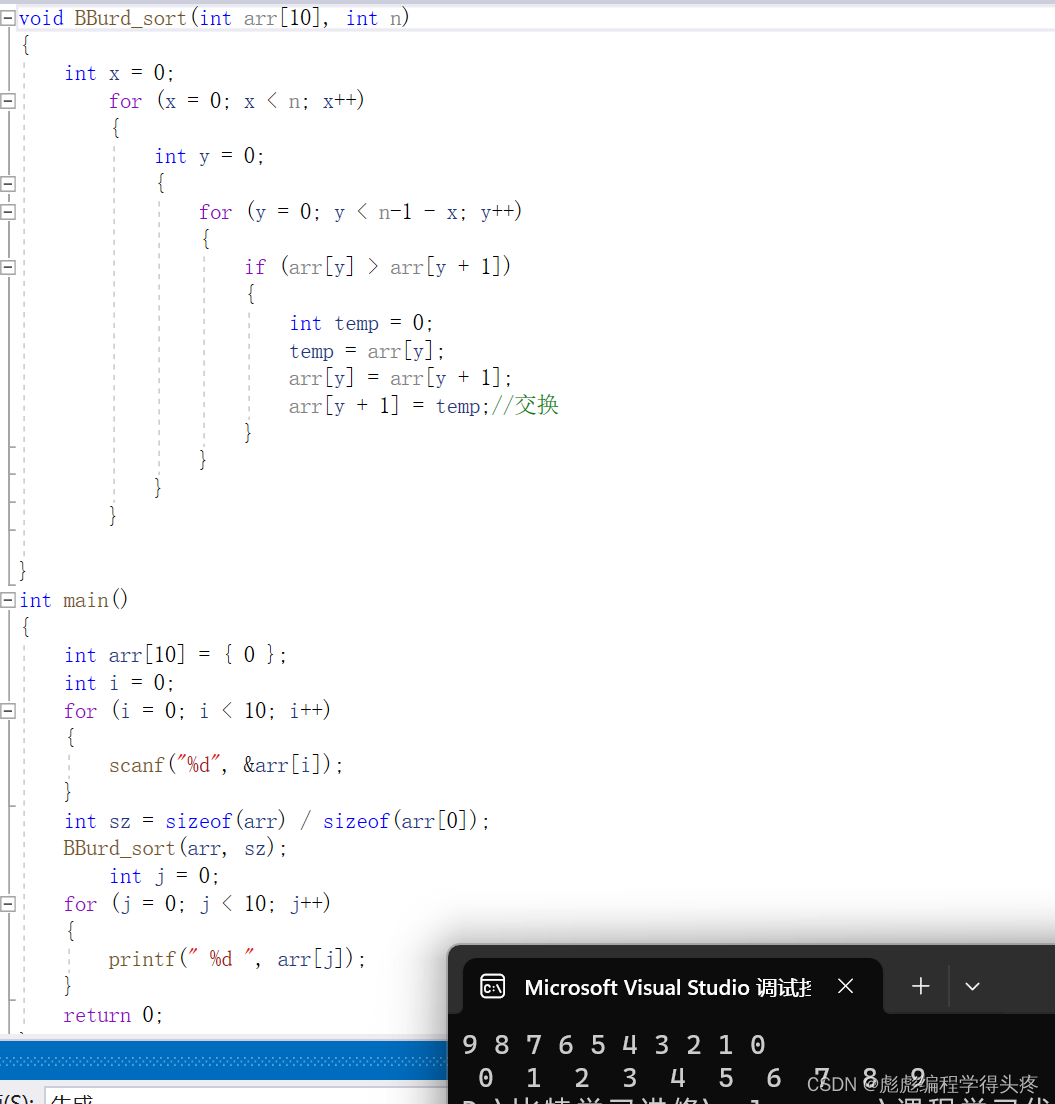
程序正常实现,附上源码。大家体验一下效果。
void BBurd_sort(int arr[10], int n)
{
int x = 0;
for (x = 0; x < n; x++)
{
int y = 0;
{
for (y = 0; y < n-1 - x; y++)
{
if (arr[y] > arr[y + 1])
{
int temp = 0;
temp = arr[y];
arr[y] = arr[y + 1];
arr[y + 1] = temp;//交换
}
}
}
}
}
int main()
{
int arr[10] = { 0 };
int i = 0;
for (i = 0; i < 10; i++)
{
scanf("%d", &arr[i]);
}
int sz = sizeof(arr) / sizeof(arr[0]);
BBurd_sort(arr, sz);
int j = 0;
for (j = 0; j < 10; j++)
{
printf(" %d ", arr[j]);
}
return 0;
}4.4 冒泡排序代码效率改进。
思考:
对于这样一个有序数列,我们如果执行的话,我们的自定义函数就还是会跑一遍,那么这样实际效率并不高。所以想能不能改进一下我我们的代码。

再次浏览原理图,我们不难发现这样一个规律,只要数据是乱序一趟下来就会有元素在发生交换。
比如:
9 1 2 3 4 5 6 7 8
这样的数据,第一趟会有元素交换,第二趟就没有。
那么我们可以这样,只要某一趟没有交换,说明此时我们的数列已经有序了就跳出
只要发生交换就继续。
那么看一下改进代码:
void BBurd_sort(int arr[10], int n)
{
int x = 0;
for (x = 0; x < n; x++)
{
int flag = 0;
int y = 0;
for (y = 0; y < n-1 - x; y++)
{
if (arr[y] > arr[y + 1])
{
int temp = 0;
temp = arr[y];
arr[y] = arr[y + 1];
arr[y + 1] = temp;//交换
flag = 1;//发生了交换就改变flag
}
}
//执行完一趟就判断一下有没有交换,有交换就继续,没有交换就直接退出,不用排序了
if (flag == 0)
{
break;
}
}
}
int main()
{
int arr[10] = { 0 };
int i = 0;
for (i = 0; i < 10; i++)
{
scanf("%d", &arr[i]);
}
int sz = sizeof(arr) / sizeof(arr[0]);
BBurd_sort(arr, sz);
int j = 0;
for (j = 0; j < 10; j++)
{
printf(" %d ", arr[j]);
}
return 0;
}5.堆排序
使用堆结构对一组数据进行排序,方便对数据进行处理。粗暴办法就是将原数组数据插入堆,再取堆数据覆盖,这种方法首先得有堆结构,其次插入数据就要额外开辟空间。
最好的方式就是直接将原数组或者原来的这组数据变成堆。将原数组直接看成一颗完全二叉树,一般都不是堆。那么就要将原数据之间调成堆----建堆
建堆不是插入数据,只是使用向上调整的思想。在原有数据上进行更改,调换。
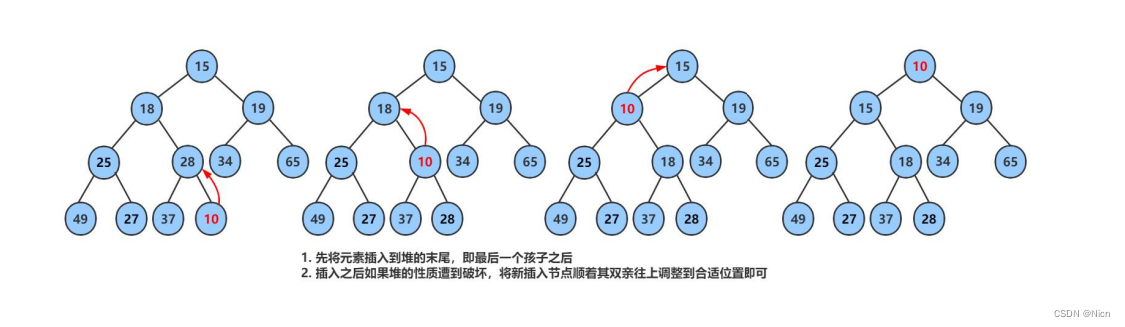
5.1升序建大堆,降序建小堆
一般我们要利用堆结构将一组数据排成升序,就建立大堆
要利用堆结构将一组数据排成降序,就建立小堆。
void HeapSort(int* a, int n)
{
//对数据进行建堆
for (int i = 0; i < n; i++)
{
AdjustUp(a, 1);
}
//堆排序---向下调整的思想
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;//让n-1个数据调整成堆选出次小
}
}5.2 建堆的时间复杂度
5.2.1 向下调整建堆
讨论最坏的时间复杂度
将下图进行建立一个大堆
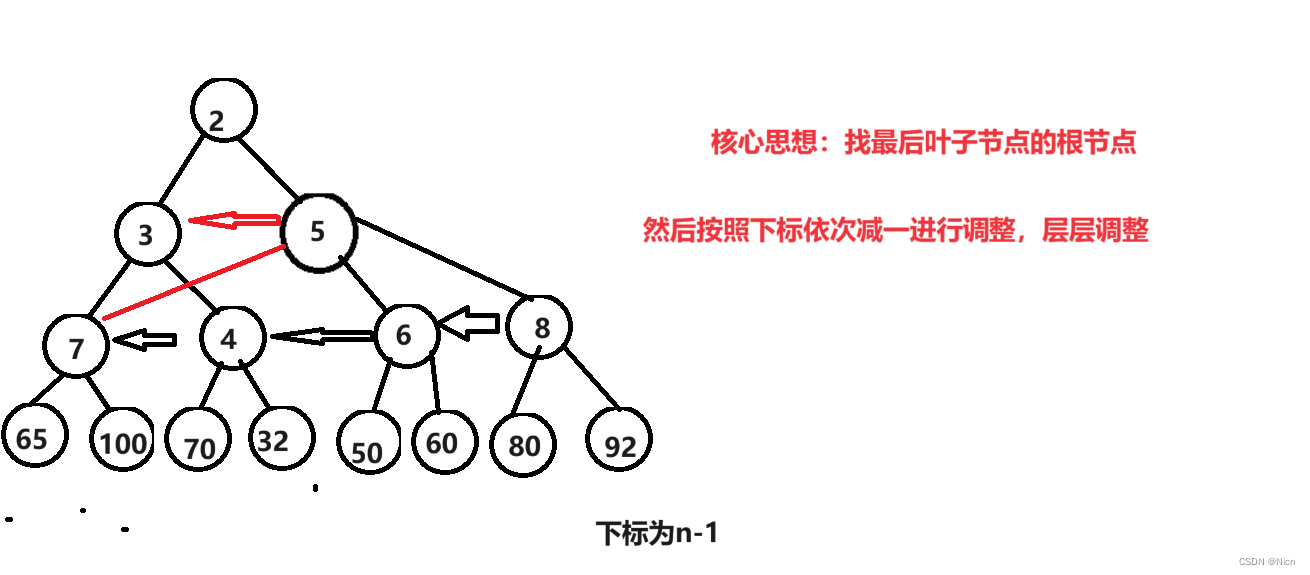
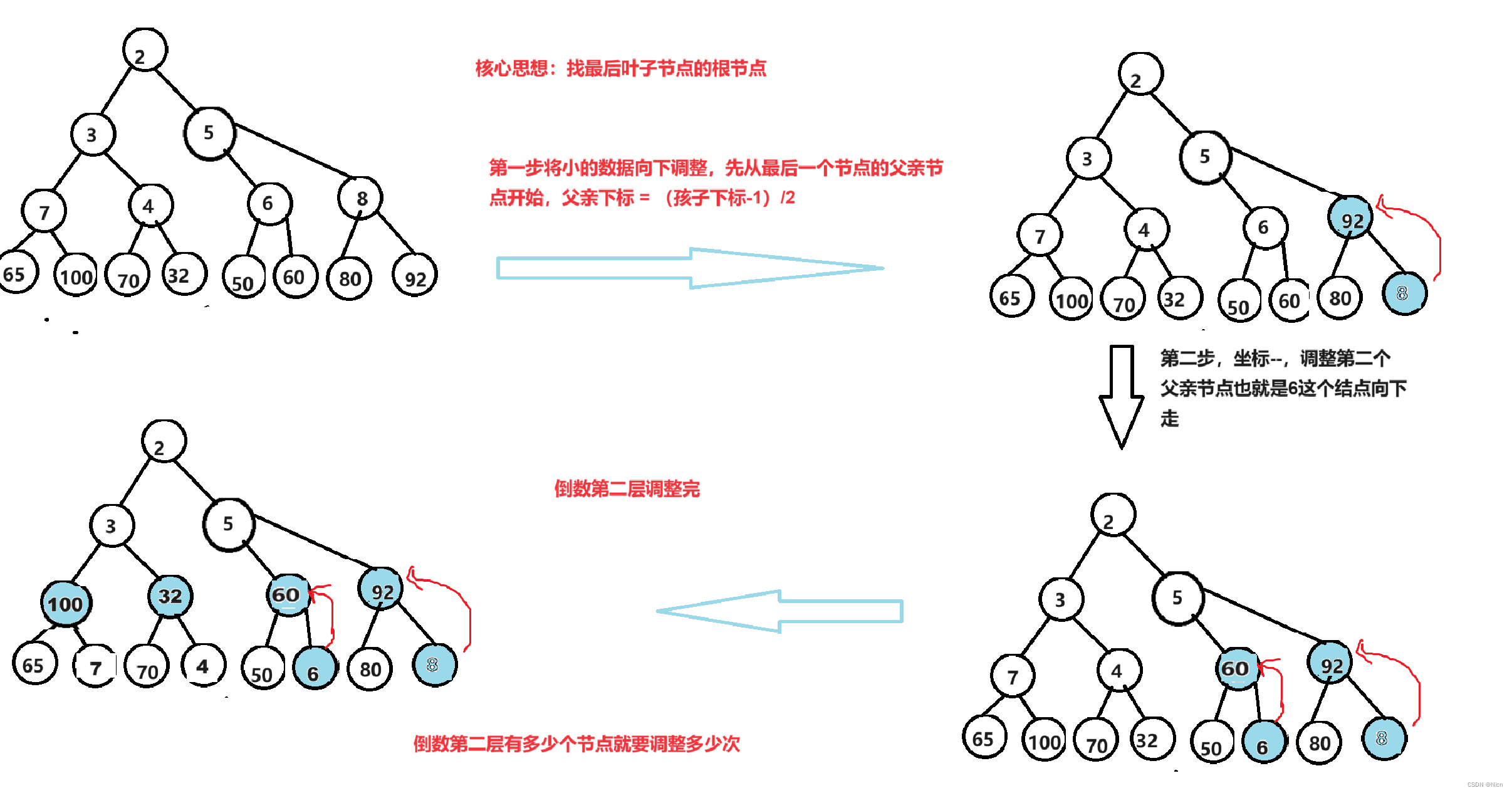
实现:
void AdjustDown(int* a, int parent, int n)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child] < a[child + 1])
{
child++;//找出左右孩子中大的一个1
}
if (a[child] >a[parent])
{
//交换
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆排序
//首先将数据建堆
//升序建大堆,降序建小堆
//采用向下调整建堆的方式时间复杂度较小
int child = n - 1;
int parent = (child - 1) / 2;
while (parent >=0)
{
AdjustDown(a, parent, n);
parent--;
}
假设有h层,这里测算的时间复杂度是最坏的情况,那么就相当于调整的是一个满二叉树的堆。
第h层 ,共有2^(h-1)个节点, 需要调整0次
第h-1层,共有2^(h-2)个节点 ,每个节点调整一次,调整:2^(h-2)*1次
第h-2层,共有2^(h-3)个节点,每个节点最坏向下调整两次,调整2^(h-3)*2次
:
:
:
第3层,共有2^(2)个节点,每个节点向下调整h-3次,调整2^(2)*(h-3)次
第2层,共有2^(1)个节点,每个节点向下调整h-2次,调整2^(1)*(h-2)次
第1层,共有2^(0)个节点,每个节点向下调整h-1次,调整2^(0)*(h-1)次
时间复杂度为:
T(h) = 2^(0)*(h-1)+2^(1)*(h-2)+2^(2)*(h-3)+…………2^(h-3)*2+2^(h-2)*1①
2T(h) = 2^(1)*(h-1)+2^(2)*(h-2)+2^(3)*(h-3)+…………2^(h-2)*2+2^(h-1)*1
②
②-①得
T(h) = 2^(1)+2^(2)……+2^(h-2)+2^(h-1)+1-h
=2^0+2^(1)+2^(2)……+2^(h-2)+2^(h-1)-h
=2^h-1-h
由于h是树的层高,与节点个数的关系是:N = 2^h-1
h = log(n+1)
所以时间复杂度为:
O(N) = N-longN+1~O(N)
5.2.2向上调整建堆

假设有h层,这里测算的时间复杂度是最坏的情况,那么就相当于调整的是一个满二叉树的堆。
第2层,共有2^1个节点,每个节点向上调整1次
第3层,共有2^2个节点,每个节点向上调整2次
:
:
:
第h-2层,共有2^(h-3)个节点,每个节点向上调整h-3次
第h-1层,共有2^(h-2)个节点,每个节点向上调整h-2次
第h层 ,共有2^(h-1)个节点,每个节点向上调整h-1次
时间复杂度为:T(h) = 2^1*1+2^2*2+2^3*3……2^(h-3)*(h-3)+2^(h-2)*(h-2)+2^(h-1)*(h-1)
2 T(h) = 2^2*1+2^3*2+2^4*3……2^(h-2)*(h-3)+2^(h-1)*(h-2)+2^(h)*(h-1)
T(h) = -2-(2^2+2^3+2^4…………2^(h-1))+2^h(h-1)
= -(2^0+2^1+2^2…………2^(h-1))+2^h(h-1)+2^0
=2^h*(h-2)+2
由于h是树的层高,与节点个数的关系是:N = 2^h-1
h = log(n+1)
T(N) = (N+1)log(N+1)-2N-1
5.3 排序实现
排序和删除的原理是一样的,先找最大/最小然后次大/次小,每次选取数据后不会将后面数据覆盖上来,否则就会导致关系全乱,可能次大数据就要重新建堆,增加了工作量了。而是通过堆顶元素和最后一个数据交换位置过后,向下调整思想,将排除刚刚调整的尾部最大数据除外的剩下数据看成堆,循环排序。
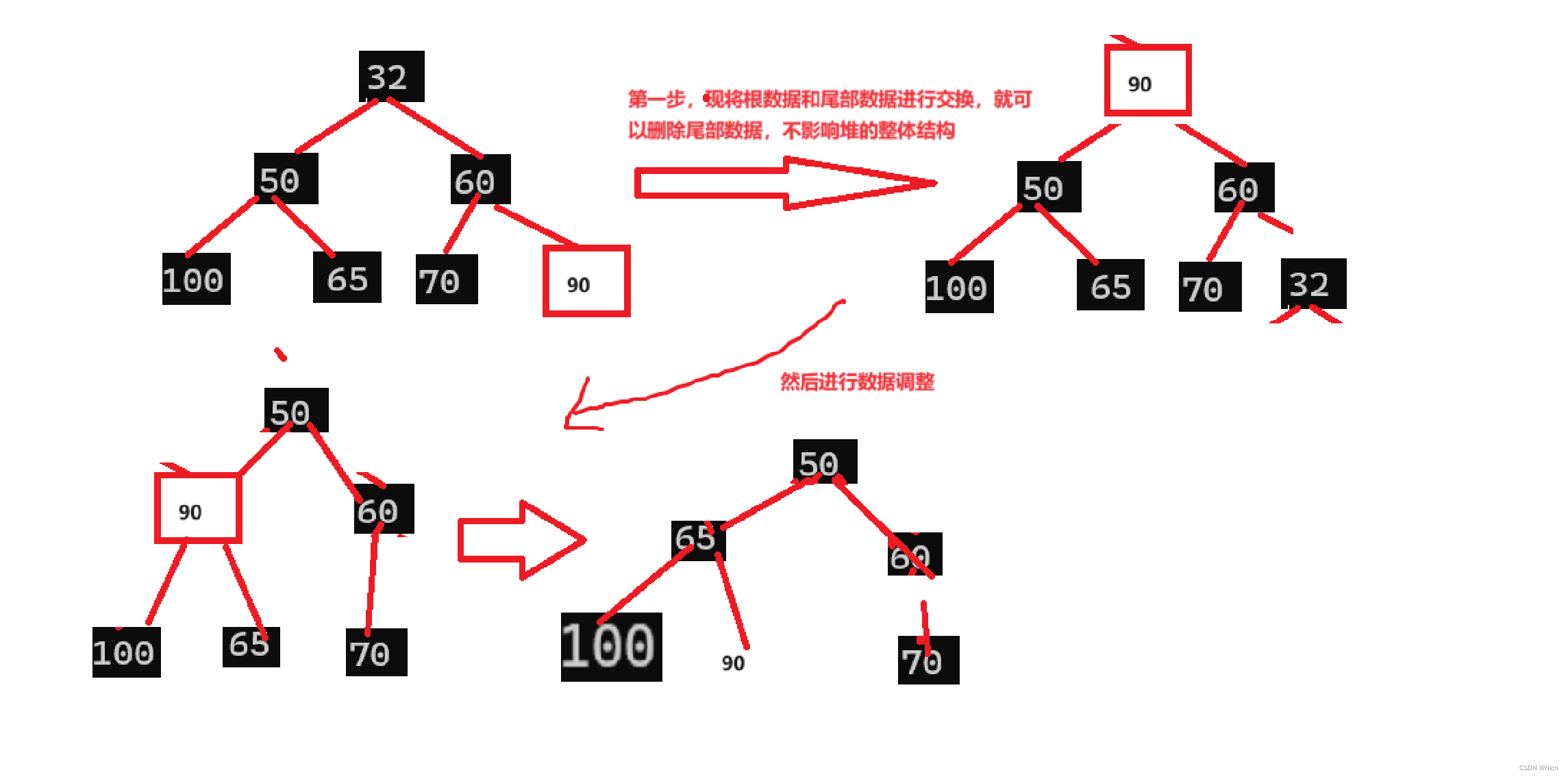
最后发现:大堆这样处理的数据最大的数据在最后,最小的在最前,小堆相反。
void AdjustDown(int* a, int parent, int n)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child] < a[child + 1])
{
child++;//找出左右孩子中大的一个1
}
if (a[child] >a[parent])
{
//交换
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆排序
void HeapSort(int* a, int n)
{
//首先将数据建堆
//升序建大堆,降序建小堆
//采用向下调整建堆的方式时间复杂度较小
int child = n - 1;
int parent = (child - 1) / 2;
while (parent >=0)
{
AdjustDown(a, parent, n);
parent--;
}
//排序
int end = n - 1;
while (end >= 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, 0, end);
end--;
}
}6.选择排序
6.1基本思想:
6.2算法演示

6.3代码实现
//选择排序
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin <end)
{
int min = begin;
int max = begin;
int i = 0;
for (i = begin+1; i <= end; i++)
{
if (a[min] > a[i])
{
min = i;
}
if (a[max] < a[i])
{
max = i;
}
}
Swap(&a[begin], &a[min]);
if (begin == max)
{
max = min;
}
Swap(&a[end], &a[max]);
end--;
begin++;
}
}
6.4时间复杂度分析
如果有10个数据: 10 9 8 7 6 5 4 3 2 1第一次:比较2(n-1次)第二次比较:2(n-3)次最后一次比较:1次总共比较:n/2次,时间复杂度为:1/4n^2
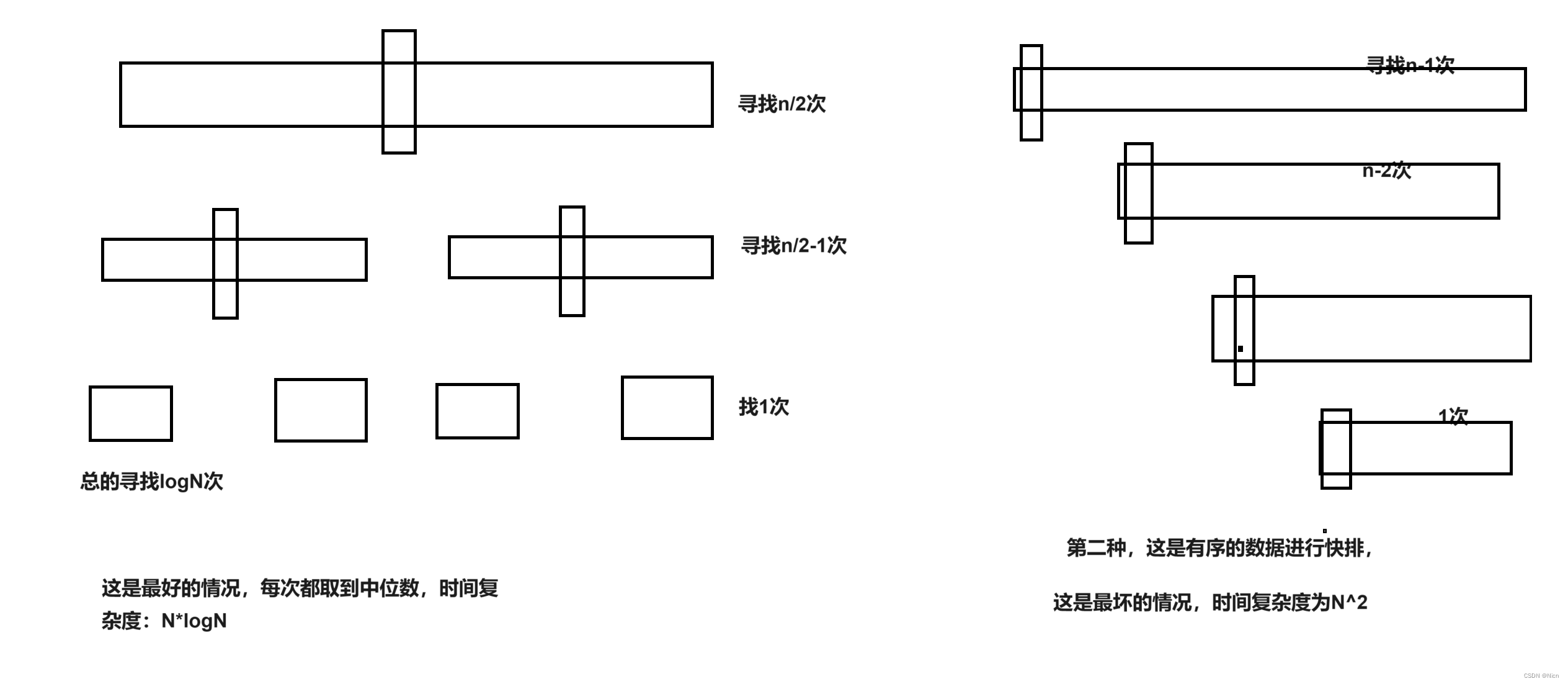
7.快速排序
算法思想:
7.1 hoare版本
单趟:
7.1.1算法图解
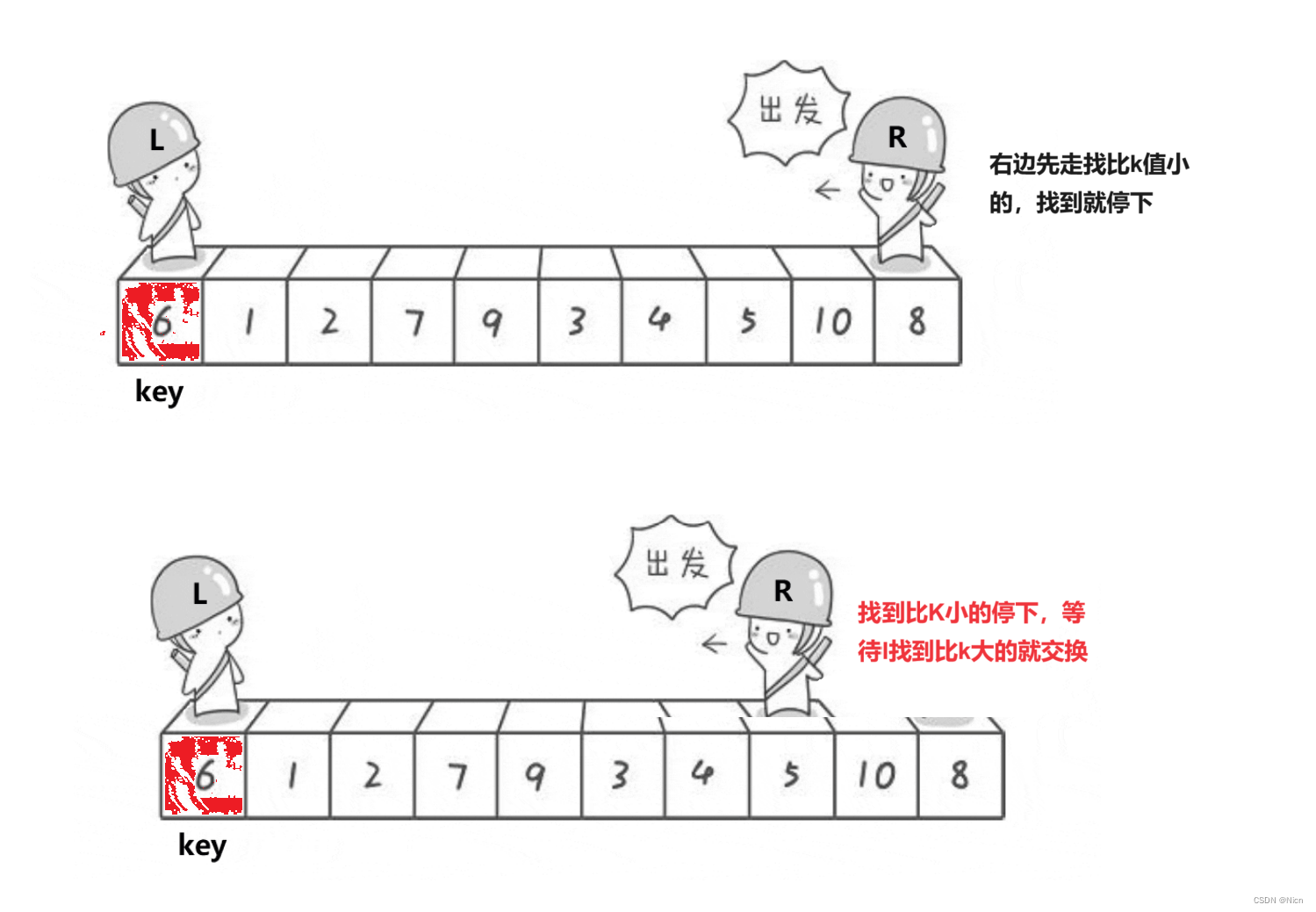
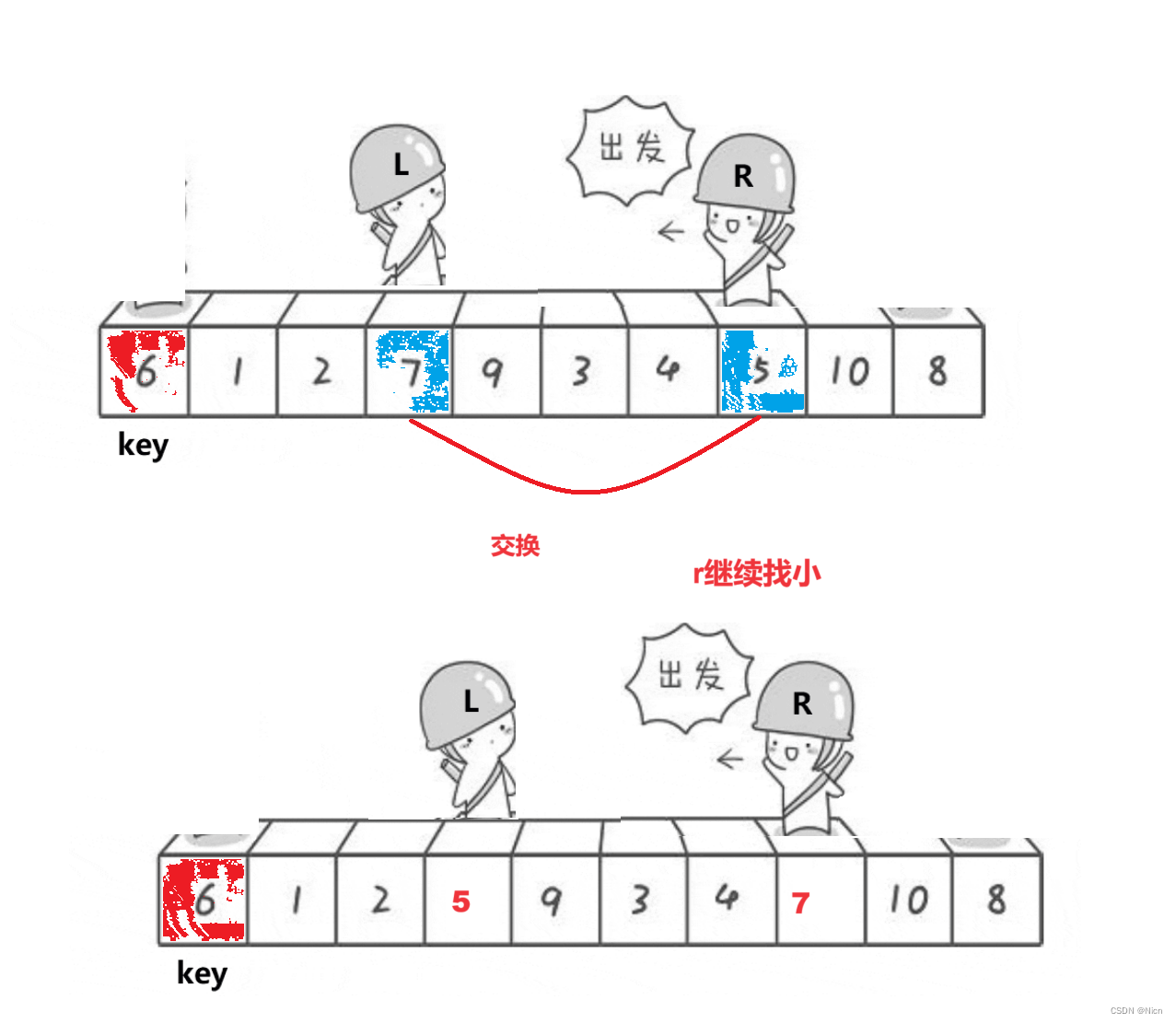
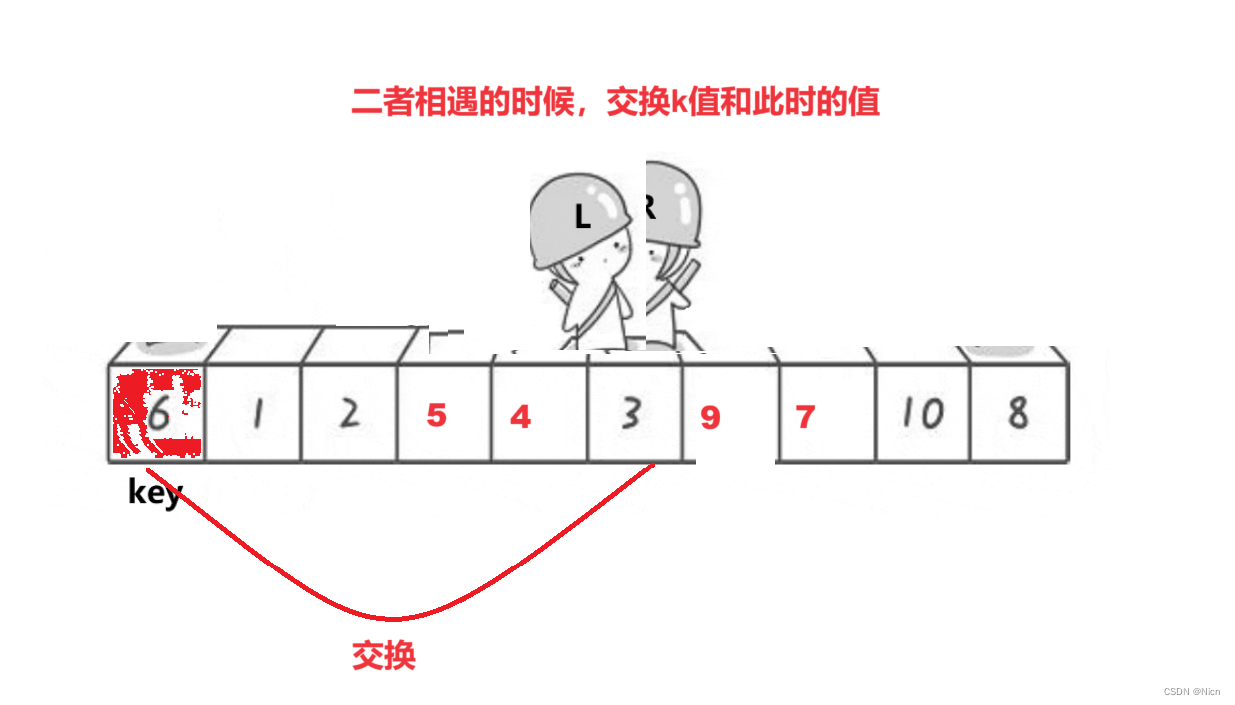
为什么相遇的位置一定是比k值小的值是因为右边先走,那么每次左边停下来的值经过交换一定是比k值大,此时r继续走,找到比k值大的数才会停下来,所以如果右边先走,停下来的地方值一定小于k,如果左边先走,停下来的地方的值一定大于k。
将上述过程递归就可以得到一个有序的序列:

7.1.2代码实现
int Partsort(int* a, int left, int right)
{
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
right--;//如果左右两边同时是key,此时如果不取等号就回陷入死循环
//再次判断left<key是因为值都比k大或者都比k小的极端情况出现越界问题,因为外层循环只判断了一次,里面的--++的循环没有判断
}
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
return left;
}
//快速排序
void QuickSort(int* a, int left,int right)
{
if (left >= right)
{
//大于为空,等于只有一个值
return;
}
int keyi = Partsort(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}7.1.3 算法优化---三数取中
为了保证我们快排的效率呢,我们试着调整一下我们选择key值的策略。
每次选取三个数中中间值的一个作为我们的key,并且将这个值换到数组的最左边:
int GetMid(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else
{
if (a[mid > a[right]])
{
return mid;
}
else if (a[left] < a[right])//mid是最小的
{
return left;
}
else
{
return right;
}
}
}
int Partsort(int* a, int left, int right)
{
int mid = GetMid(a, left, right);
Swap(&a[left], &a[mid]);
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
right--;//如果左右两边同时是key,此时如果不取等号就回陷入死循环
//再次判断left<key是因为值都比k大或者都比k小的极端情况出现越界问题,因为外层循环只判断了一次,里面的--++的循环没有判断
}
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
return left;
}
//快速排序
void QuickSort(int* a, int left,int right)
{
if (left >= right)
{
//大于为空,等于只有一个值
return;
}
int keyi = Partsort(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}这样我们的逆序排序这种对于快排最坏的情况就变成最好的情况,十万个数据1毫秒就可以排好。
7.2挖坑法快排
7.2.1算法图解
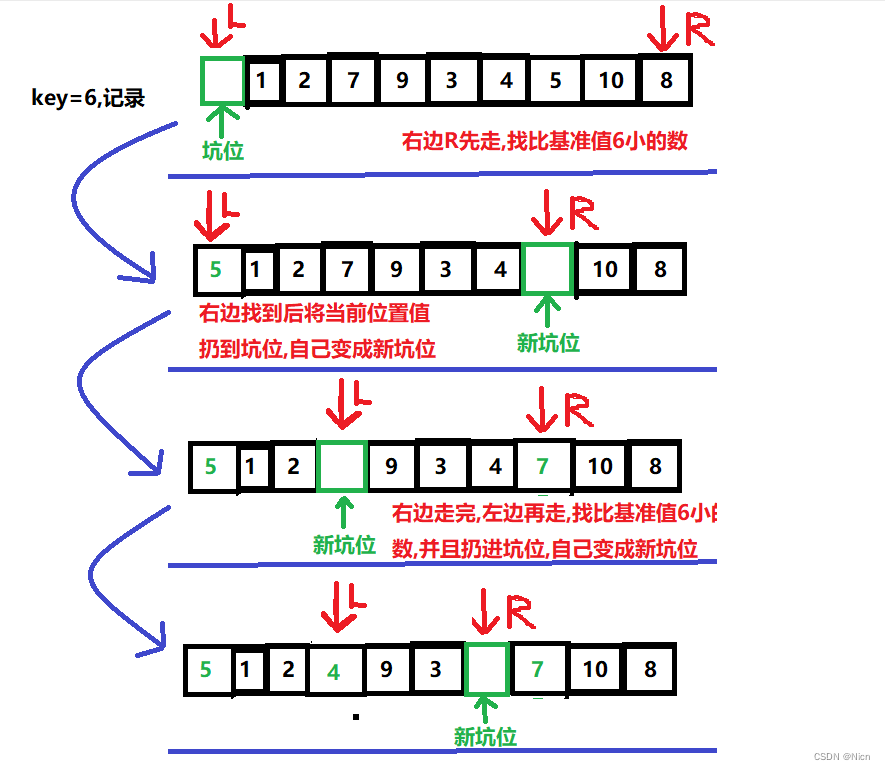
7.2.2 代码实现
//挖坑法
int Partsort2(int* a, int left, int right)
{
int mid = GetMid(a, left, right);
Swap(&a[left], &a[mid]);
int ken = a[left];
int hole = left;
while (left < right)
{
while (left < right && a[right] >= ken)
{
right--;
}
a[hole] = a[right];
hole = right;
while (left < right && a[left] <= a[ken])
{
left++;
}
a[hole] = a[left];
hole= left;
}
a[hole] = ken;
return hole;
}
7.3 前后指针法
逻辑:cur找比key值小的值,然后prev遇到比key值大的就停下来,直到cur遇到比key值小的值过后就交换。
prev:
在cur没有遇到比key值大的值的时候,prev紧紧的跟着cur
在cur遇到比key值大的值的时候,prev就停下来了,prev在比key大的一组值的前面。
//前后指针
int Partsort3(int* a, int left, int right)
{
int mid = GetMid(a, left, right);
Swap(&a[left], &a[mid]);
int keyi = left;
int prev = left;
int cur = prev + 1;
while (cur <= right)
{
if (a[cur] < a[keyi]&&prev++ != cur)//防止开始位置自己跟自己交换
{
Swap(&a[prev++], &a[cur]);
}
cur++;
}
Swap(&a[prev], &a[keyi]);
return prev;
}7.4快速排序进一步优化
按照上面的方法实际主题来说,大思想就是递归,递归是有消耗的,而且,最后几层的递归往往是最大的,如果当递归区间的数值减少到一定程度,我们就不递归了,特别是到最后一两层的时候,那么排序的效率就会有提升。
//快速排序
void QuickSort(int* a, int left,int right)
{
if (left >= right)
{
//大于为空,等于只有一个值
return;
}
if ((right - left + 1) > 10)
{
int keyi = Partsort(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
else
{
InserPort(a + left, right - left + 1);
}
}
小区间优化,编译器对递归优化也比较好,小区间不在递归,降低递归次数
7.5快速排序非递归写法
使用栈保存每次划分的区间
void QuickSortNonR(int* a, int left, int right)
{
Stack st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (StackEmpty(&st) != 0)
{
right = StackTop(&st);
StackPop(&st);
left = StackTop(&st);
StackPop(&st);
if(right - left <= 1)
continue;
int div = PartSort1(a, left, right);
// 以基准值为分割点,形成左右两部分:[left, div) 和 [div+1, right)
StackPush(&st, div+1);
StackPush(&st, right);
StackPush(&st, left);
StackPush(&st, div);
}
StackDestroy(&s);
} 
8.归并排序
排序思想:

public class Sort {
public static void main(String[] args) {
int[] a={10,4,6,3,8,2,5,7};
//归并排序
mergeSort(a,0,a.length-1);
}
private static void mergeSort(int[] a, int left, int right) {
if(left<right){
int middle = (left+right)/2;
//对左边进行递归
mergeSort(a, left, middle);
//对右边进行递归
mergeSort(a, middle+1, right);
//合并
merge(a,left,middle,right);
}
}
private static void merge(int[] a, int left, int middle, int right) {
int[] tmpArr = new int[a.length];
int mid = middle+1; //右边的起始位置
int tmp = left;
int third = left;
while(left<=middle && mid<=right){
//从两个数组中选取较小的数放入中间数组
if(a[left]<=a[mid]){
tmpArr[third++] = a[left++];
}else{
tmpArr[third++] = a[mid++];
}
}
//将剩余的部分放入中间数组
while(left<=middle){
tmpArr[third++] = a[left++];
}
while(mid<=right){
tmpArr[third++] = a[mid++];
}
//将中间数组复制回原数组
while(tmp<=right){
a[tmp] = tmpArr[tmp++];
}
}
}
9.计数排序
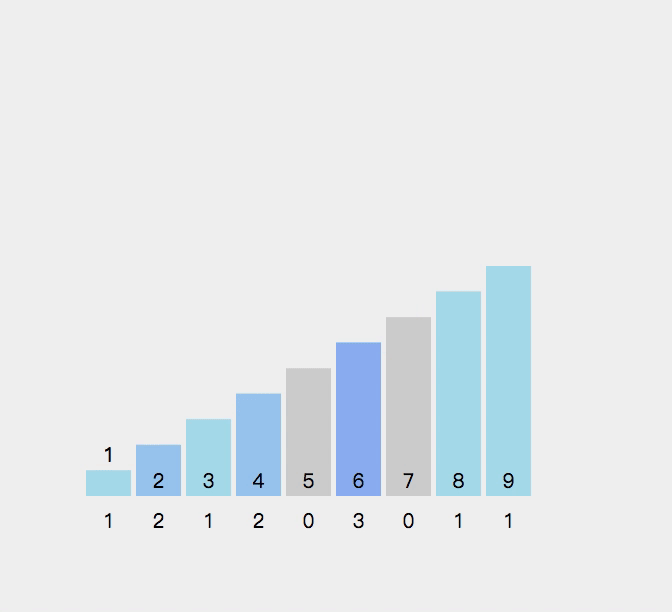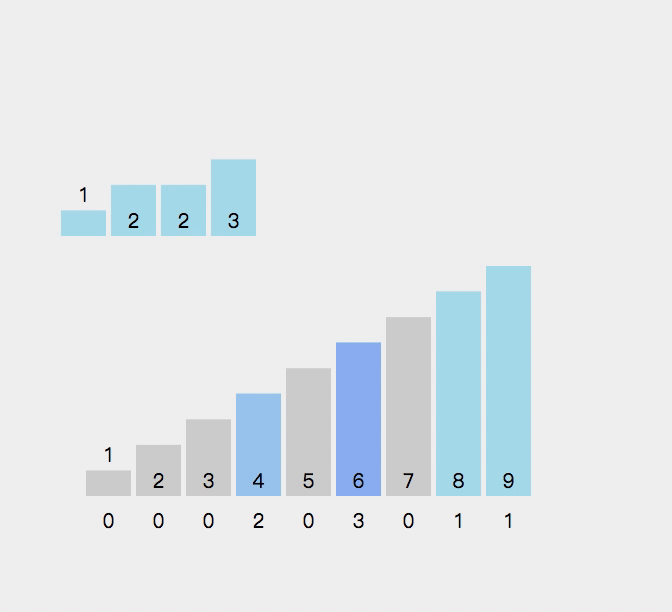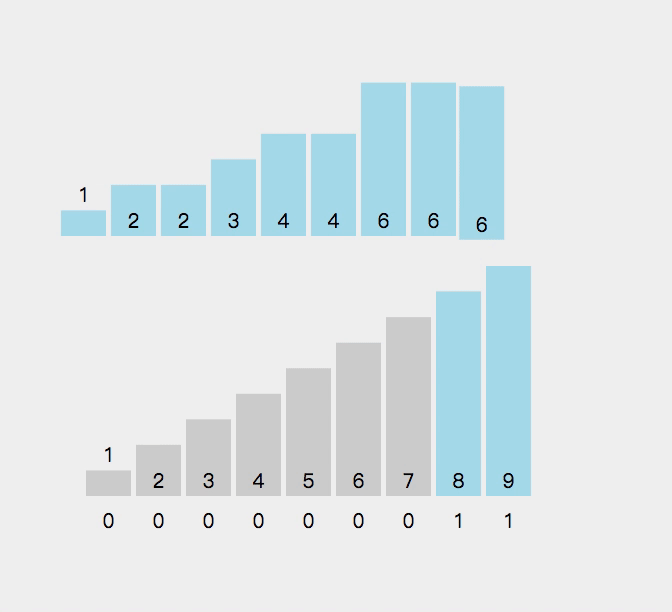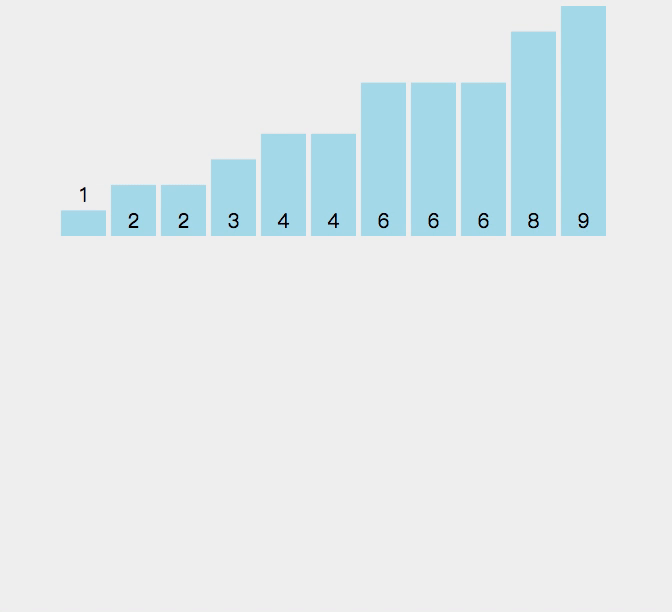
//计数排序
void MergeSort(int* a, int n)
{
int min = a[0], max = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] < min)
{
min = a[i];
}
if (a[i] > max)
{
max = a[i];
}
}
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
if (count == NULL)
{
perror("malloc fail");
return;
}
memset(count, 0, sizeof(int) * range);
//统计数据出现的个数
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
//排序
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
}
10.结语
以上就是本期所有内容,耗时半周,应该整理得比较全面,越往后面的排序代码实现就越难。知识含量蛮多,大家可以配合解释和原码运行理解。创作不易,大家如果觉得还可以的话,欢迎大家三连,有问题的地方欢迎大家指正,一起交流学习,一起成长,我是Nicn,正在c++方向前行的奋斗者,数据结构内容持续更新中,感谢大家的关注与喜欢。