深入理解数据结构(3)：栈和队列详解

news2024/11/27 10:19:23

标头风景图片

  • 文章主题：顺序表和链表详解🌱
  • 所属专栏：深入理解数据结构📘
  • 作者简介：更新有关深入理解数据结构知识的博主一枚，记录分享自己对数据结构的深入解读。😄
  • 个人主页：[₽]的个人主页🔥🔥

栈和队列详解

  • 前言
  • 栈
    • 栈的概念及结构
    • 栈的实现
  • 队列
    • 队列的概念及结构
    • 队列的实现
  • 结语

前言

上文我们已经讲完了线性表中最基本的、最常用的顺序表和链表，这一次博主为大家带来基于顺序表和链表实现的线性表中也是十分常用的数据结构栈和队列的详解，希望能够让你对数据结构有一个更加深入的理解。

栈

栈的概念及结构

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈/弹栈。出数据也在栈顶。
栈的后进先出

栈的实现

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小，最简单。
栈的数组实现
静态数组栈
下面是定长的静态栈的结构，实际中一般不实用，所以我们主要实现下面的支持动态增长的栈

// 下面是定长的静态栈的结构，实际中一般不实用，所以我们主要实现下面的支持动态增长的栈
typedef int STDataType;
#define N 10
typedef struct Stack
{
 STDataType _a[N];
 int _top; // 栈顶
}Stack;

动态数组栈
Stack.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
	STDataType* _a;
	int _top;		// 栈顶
	int _capacity;  // 容量 
}Stack;
// 初始化栈 
void StackInit(Stack* ps);
// 入栈 
void StackPush(Stack* ps, STDataType data);
// 出栈 
void StackPop(Stack* ps);
// 获取栈顶元素 
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数 
int StackSize(Stack* ps);
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
int StackEmpty(Stack* ps);
// 销毁栈 
void StackDestroy(Stack* ps);

Stack.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Stack.h"
void StackInit(Stack* ps)
{
	assert(ps);
	// 栈区数组未创建，赋成NULL
	ps->_a = NULL;
	ps->_capacity = 0;
	// 表示top指向栈顶元素
	ps->_top = -1;
	// 表示top指向栈顶元素的下一个
	//ps->_top = 0
}
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);
	// 栈区数据已满，扩容
	if (ps->_top + 1 == ps->_capacity)
	{
		// 确定扩容后的新容量，如果是 0 就扩容为 4 ，如果已经扩过容了就将容量在增加一个原来这么多，即扩大为原来的两倍
		int newcapacity = ps->_capacity == 0 ? 4 : ps->_capacity * 2;
		// 扩容
		STDataType* tmp = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
		// 扩容失败打印失败原因后返回
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		// 未失败将容量更新成新容量，数据指针更新成新指针
		ps->_capacity = newcapacity;
		ps->_a = tmp;
	}
	// 插入数据
	ps->_top++;
	ps->_a[ps->_top] = data;
}
void StackPop(Stack* ps)
{
	assert(ps);
	// 栈不为空时才能删除数据
	assert(ps->_top + 1 > 0);
	// 栈顶元素坐标下移，删除数据
	ps->_top--;
}
STDataType StackTop(Stack* ps)
{
	assert(ps);
	// 不为空，为空弹不出数据来进行访问，并且访问会导致数组越界
	assert(ps->_top + 1 > 0);
	// 返回栈顶元素值
	return ps->_a[ps->_top];
}
int StackSize(Stack* ps)
{
	assert(ps);
	// 返回栈中有效元素个数（栈顶元素 +1 即为栈中有效元素个数）
	return ps->_top + 1;
}
int StackEmpty(Stack* ps)
{
	assert(ps);
	// 为空则返回非 0 的真
	return ps->_top + 1 == 0;
}
void StackDestroy(Stack* ps)
{
	assert(ps);
	// 数据内存释放，再将记录数据的各值清空
	free(ps->_a);
	ps->_a = NULL;
	ps->_capacity = 0;
	ps->_top = -1;
}

Test.c

#include "Stack.h"
void StackTest1()
{
	// 初始化栈
	Stack S1;
	StackInit(&S1);

	// 数据入栈
	StackPush(&S1, 1);
	StackPush(&S1, 2);
	StackPush(&S1, 3);
	StackPush(&S1, 4);
	StackPush(&S1, 5);

	// 销毁栈
	StackDestroy(&S1);

	// 检测是否销毁成功
	if (S1._a == NULL && S1._capacity == 0 && S1._top == -1)
		printf("销毁成功！\n");
	else
		printf("销毁失败。\n");
}
void StackTest2()
{
	// 初始化栈
	Stack S1;
	StackInit(&S1);

	// 数据入栈
	StackPush(&S1, 1);
	StackPush(&S1, 2);
	StackPush(&S1, 3);
	StackPush(&S1, 4);
	StackPush(&S1, 5);

	// 从栈顶读取数据后弹出栈中数据
	while (!StackEmpty(&S1))
	{
		printf("%d ", StackTop(&S1));
		StackPop(&S1);
	}
	printf("\n");

	// 销毁栈
	StackDestroy(&S1);
}
void StackTest3()
{
	// 初始化栈
	Stack S1;
	StackInit(&S1);

	// 栈为空时也弹出数据
	StackPop(&S1);

	// 销毁栈
	StackDestroy(&S1);
}
int main()
{
	StackTest3();
	return 0;
}

队列

队列的概念及结构

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾 出队列：进行删除操作的一端称为队头
入队：队列的插入操作叫做入队，入数据在队尾。
出队：队列的删除操作叫做出队。出数据在队头。
（栈和对列都是将出数据的地方叫作顶/头）
队列的出队入队

队列的实现

队列也可以数组和链表的结构实现，使用链表（带头的单链表）的结构实现更优一些(时间复杂度O(1)，比数组来说在队头删除数据更加简洁)，因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低(时间复杂度为O(N))。
带头单链表实现的队列
队列
Queue.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

typedef int QDataType;
// 链式结构：表示队列 
typedef struct QListNode
{
	struct QListNode* _next;
	QDataType _data;
}QNode;

// 队列的结构 
typedef struct Queue
{
	QNode* _front;
	QNode* _rear;
	int _size;
}Queue;

// 初始化队列 
void QueueInit(Queue* q);
// 销毁队列 
void QueueDestroy(Queue* q);
// 队尾入队列 
void QueuePush(Queue* q, QDataType data);
// 队头出队列 
void QueuePop(Queue* q);
// 获取队列头部元素 
QDataType QueueFront(Queue* q);
// 获取队列队尾元素 
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数 
int QueueSize(Queue* q);
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q);

Queue.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Queue.h"
void QueueInit(Queue* q)
{
	assert(q);
	// 首尾指针都赋成NULL，元素个数赋0
	q->_front = q->_rear = NULL;
	q->_size = 0;
}
void QueueDestroy(Queue* q)
{
	assert(q);
	// 释放队列数据内存
	QNode* cur = q->_front;
	while (cur)
	{
		QNode* tmp = cur;
		cur = cur->_next;
		free(tmp);
	}
	// 将队列中的首尾指针数据赋成NULL，队列元素个数也置为0
	q->_front = q->_rear = NULL;
	q->_size = 0;
}
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	// 创建新节点
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("maloc fail");
		return;
	}
	newnode->_data = data;
	newnode->_next = NULL;
	// 无节点
	if (q->_front == NULL)
	{
		q->_front = q->_rear = newnode;
	}
	// 有节点
	else
	{
		q->_rear->_next = newnode;
		q->_rear = newnode;
	}
	// 队尾入数据时总元素个数加一
	q->_size++;
}
void QueuePop(Queue* q)
{
	assert(q);
	// 无节点
	assert(q->_front);
	// 有节点
	QNode* tmp = q->_front;
	q->_front = q->_front->_next;
	free(tmp);
	// 一个节点时，尾指针因为释放节点变成野指针，需要置空
	if (q->_front == NULL)
		q->_rear = NULL;
	// 队头出数据时总元素个数减一
	q->_size--;
}
QDataType QueueFront(Queue* q)
{
	assert(q);
	// 无节点
	assert(q->_front);
	// 有节点
	return q->_front->_data;
}
QDataType QueueBack(Queue* q)
{
	assert(q);
	// 无节点
	assert(q->_front);
	// 有节点
	return q->_rear->_data;
}
int QueueSize(Queue* q)
{
	assert(q);
	// 直接将储存队列主要数据的结构体中的元素个数拿出来返回
	return q->_size;
}
int QueueEmpty(Queue* q)
{
	assert(q);
	return q->_size == 0;
}

Test.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Queue.h"
void QueueTest1()
{
	// 队列初始化
	Queue Q1;
	QueueInit(&Q1);

	// 队尾入数据
	QueuePush(&Q1, 1);
	QueuePush(&Q1, 2);
	QueuePush(&Q1, 3);
	QueuePush(&Q1, 4);
	QueuePush(&Q1, 5);

	// 销毁队列
	QueueDestroy(&Q1);

	if (Q1._front == NULL && Q1._rear == NULL && Q1._size == 0)
		printf("销毁成功！\n");
	else
		printf("销毁失败。\n");
}

void QueueTest2()
{
	// 队列初始化
	Queue Q1;
	QueueInit(&Q1);

	// 队尾入数据
	QueuePush(&Q1, 1);
	QueuePush(&Q1, 2);
	QueuePush(&Q1, 3);
	QueuePush(&Q1, 4);
	QueuePush(&Q1, 5);

	// 打印队列中的数据
	printf("Queue: \n");
	while (!QueueEmpty(&Q1))
	{
		printf("%d ", QueueFront(&Q1));
		QueuePop(&Q1);
	}
	printf("\n");

	// 销毁队列
	QueueDestroy(&Q1);
}

void QueueTest3()
{
	// 队列初始化
	Queue Q1;
	QueueInit(&Q1);

	// 队尾入数据
	QueuePush(&Q1, 1);
	QueuePush(&Q1, 2);
	QueuePush(&Q1, 3);
	QueuePush(&Q1, 4);
	QueuePush(&Q1, 5);

	// 打印队列中的数据
	printf("Queue: \n");
	while (!QueueEmpty(&Q1))
	{
		printf("%d ", QueueFront(&Q1));
		QueuePop(&Q1);
	}
	printf("\n");

	// 无节点从队列中弹出数据
	QueuePop(&Q1);

	// 销毁队列
	QueueDestroy(&Q1);
}

void QueueTest4()
{
	// 队列初始化
	Queue Q1;
	QueueInit(&Q1);

	// 队尾入数据
	QueuePush(&Q1, 1);
	QueuePush(&Q1, 2);
	QueuePush(&Q1, 3);
	QueuePush(&Q1, 4);
	QueuePush(&Q1, 5);

	// 打印队尾中的数据
	printf("BackNum: \n%d\n", QueueBack(&Q1));

	// 打印队列中的数据
	printf("Queue: \n");
	while (!QueueEmpty(&Q1))
	{
		printf("%d ", QueueFront(&Q1));
		QueuePop(&Q1);
	}
	printf("\n");

	// 销毁队列
	QueueDestroy(&Q1);
}

void QueueTest5()
{
	// 队列初始化
	Queue Q1;
	QueueInit(&Q1);

	// 队尾入数据
	QueuePush(&Q1, 1);
	QueuePush(&Q1, 2);
	QueuePush(&Q1, 3);
	QueuePush(&Q1, 4);
	QueuePush(&Q1, 5);

	// 打印队列中的数据个数
	printf("QueueSize: \n%d\n", QueueSize(&Q1));

	// 打印队列中的数据
	printf("Queue: \n");
	while (!QueueEmpty(&Q1))
	{
		printf("%d ", QueueFront(&Q1));
		QueuePop(&Q1);
	}
	printf("\n");

	// 销毁队列
	QueueDestroy(&Q1);
}

int main()
{
	QueueTest5();
	return 0;
}

环形队列
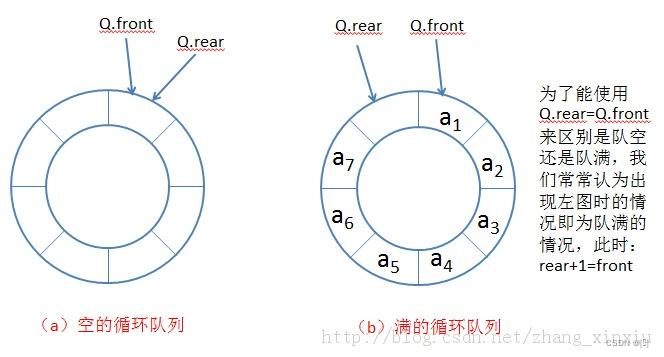
另外扩展了解一下，实际中我们有时还会使用一种队列叫循环队列。如操作系统中的生产者消费者模型中就会使用循环队列。环形队列可以使用数组实现，也可以使用循环链表实现（差别不是很大，并且环形队列的元素个数是固定的，但也可以不是在栈区的静态数组实现的，其可用在动态区用长度不变的数组来实现内存大小不变的效果，可理解成动态数组大小不变所实现的仿静态效果，并且虽逻辑结构上两种环形队列都相接，数组型的环形队列物理结构上首尾不相接，链表物理结构上相接）。
环形队列逻辑图
通常为区分队头和队尾，会在数组中多加一个元素来既防止数组越界，又能够解决因空和满索引条件相同而造成无法判断的假溢出问题（此时环形队列容量为数组总元素个数减一）：
数组环形队列实现的底层逻辑图

结语

以上就是博主对栈和队列的详解，😄希望对你的数据结构的学习有所帮助！看都看到这了，点个小小的赞或者关注一下吧（当然三连也可以~），你的支持就是博主更新最大的动力！让我们一起成长，共同进步！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1558462.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

吴恩达机器学习笔记 三十一 K-means算法及优化目标 成本函数

吴恩达机器学习笔记 三十一 K-means算法及优化目标 成本函数

随机初始化 K 个集群质心&#xff0c;这里设质心个数为2 第一步&#xff1a;分配点给集群质心 对 m 个 点&#xff0c;每个点对应的质心为 c(i) ,若离红色的质心近&#xff0c;则 c(i) 的值为1&#xff0c;否则为2。计算距离用的是L2范式。 第二步&#xff1a;移动集群质心 …
阅读更多...
Verilog语法回顾--用户定义原语

Verilog语法回顾--用户定义原语

目录 用户定义原语 UDP定义 UDP状态表 状态表符号 组合UDP 电平敏感UDP 沿敏感时序UDP 参考《Verilog 编程艺术》魏家明著 用户定义原语 用户定义原语&#xff08;User-defined primitive&#xff0c;UDP&#xff09;是一种模拟硬件技术&#xff0c;可以通过设计新的原…
阅读更多...
Yolov7 Reid【附代码，行人重识别，可做跨视频人员检测】

Yolov7 Reid【附代码，行人重识别，可做跨视频人员检测】

本项目使用Yolov7Reid实现的行人重识别功能&#xff0c;可做跨视频人员检测。 应用场景&#xff1a; 可根据行人的穿着、体貌等特征的Reid算法在视频中进行检索&#xff0c;可以把这个人在各个不同摄像头出现时检测出来。可应用于犯罪嫌疑人检索、寻找走失儿童等。支持GUI界面…
阅读更多...
Python API(happybase)操作Hbase案例

Python API(happybase)操作Hbase案例

一、Windows下安装Python库&#xff1a;happybase pip install happybase -i https://pypi.tuna.tsinghua.edu.cn/simple 二、 开启HBase的Thrift服务 想要使用Python API连接HBase&#xff0c;需要开启HBase的Thrift服务。所以&#xff0c;在Linux服务器上&#xff0c;执行如…
阅读更多...
scikit learn数据预处理学习笔记

scikit learn数据预处理学习笔记

数据集及基本操作 1&#xff09;数据集的组成 数据集由特征(feature)与标签(label)构成。 特征是输入数据。 什么是特征&#xff08;Features&#xff09;: 机器学习中输入数据&#xff0c;被称为特征。通常特征不止1个&#xff0c;可以用 n 维向量表示n个特征。 Features 数…
阅读更多...
设备树语法

设备树语法

设备树语法 1 Devicetree格式1.1 DTS文件格式1.2 node格式1.3 properties格式 2 dts文件包好desi文件3 常用的 属性 properties3.1 #address-cells、#size-cells3.2 compatible3.3 model3.4 status3.5 reg&#xff08;设备不同reg属性的含义就不同&#xff09;3.6 name、device…
阅读更多...
链式前向星解析

链式前向星解析

树形DP涉及到图存储&#xff0c;先复习一下链式前向星存储图&#xff0c;便于理解上篇的树形DP。对于图数据结构的存储&#xff0c;我们除了采用邻接矩阵&#xff08;消耗空间&#xff0c;不常用&#xff09;、邻接表&#xff0c;还有一种方法就是链式前向星。 链式前向星存储图…
阅读更多...
数据结构——线性表(一）

数据结构——线性表(一）

线性表&#xff0c;顾名思义&#xff0c;是具有像线一样的性质的表。如同学生们在操场上排队&#xff0c;一个跟着一个排队&#xff0c;有一个打头&#xff0c;有一个收尾&#xff0c;在其中的学生都知道前一个是谁&#xff0c;后一个是谁&#xff0c;这样就像一根线将他们都串…
阅读更多...
[HNCTF 2022 WEEK2]来解个方程?

[HNCTF 2022 WEEK2]来解个方程?

标准的Z3题&#xff0c;可以拿来当模版题 题目逻辑很简单 直接看check from z3 import * # 初始化求解器 s Solver() # 定义6个未知数 n 24 x [Int(s str(i)) for i in range(0,24)] s.add(245 * x[6] 395 * x[5 ] 3541 * x[4 ] 2051 * x[3 ] 3201 * x[2 ] 1345 * x[7 ] 8…
阅读更多...
中制交通安全统筹闪耀资本市场，成功上市引领行业新篇章

中制交通安全统筹闪耀资本市场，成功上市引领行业新篇章

3月30日上午,随着上市钟声的敲响,中制(海南)交通安全统筹服务有限公司(股票代码:HK 31598)在香港股权交易展示中心挂牌上市,中制交通安全统筹董事长熊辉、联合创始人兼CEO张国伟、董事石杰等公司高管、股东、客户、合作伙伴出席挂牌仪式,共同见证敲钟上市,这也使中制交通安全统…
阅读更多...
PonyAi Planning-横纵向轨迹规划

PonyAi Planning-横纵向轨迹规划

PonyAi Planning-横纵向轨迹规划 轨迹规划的探索和挑战 轨迹规划的概念安全舒适两不误&#xff1a;探讨优化算法在规划控制中的应用 轨迹规划的概念 决策 横向规划 纵向规划 优化算法在规划&#xff08;Planning&#xff09;中的应用 附赠自动驾驶学习资料和量产经验…
阅读更多...
PP-YOLOE： An evolved version of YOLO

PP-YOLOE： An evolved version of YOLO

摘要 我们在之前 PP-YOLOv2 的基础上进行了优化&#xff0c;使用 无锚 范式&#xff0c;更强大的主干和颈部配备了 CSPRepResStage 。 ET-head 和动态标签分配算法 TAL 。 1 、介绍 受 YOLOX 的启发&#xff0c;我们进一步优化了之前的工作 PP-YOLOv2 。 PP-YOLOv2 是一款高…
阅读更多...
使用hping3网络工具构造TCP/IP数据包和进行DDos攻击

使用hping3网络工具构造TCP/IP数据包和进行DDos攻击

1 概述 hping3是一个强大的命令行工具&#xff0c;用于生成、发送和解析TCP/IP协议的数据包。它是开源的网络安全工具&#xff0c;由Salvatore Sanfilippo开发&#xff0c;主要应用于网络审计、安全测试和故障排查等领域。hping3不仅可以作为普通的网络连通性检测工具&#xf…
阅读更多...
深入理解数据结构(2)：顺序表和链表详解

深入理解数据结构(2)：顺序表和链表详解

文章主题&#xff1a;顺序表和链表详解&#x1f331;所属专栏&#xff1a;深入理解数据结构&#x1f4d8;作者简介&#xff1a;更新有关深入理解数据结构知识的博主一枚&#xff0c;记录分享自己对数据结构的深入解读。&#x1f604;个人主页&#xff1a;[₽]的个人主页&#x…
阅读更多...
数据结构——lesson12排序之归并排序

数据结构——lesson12排序之归并排序

&#x1f49e;&#x1f49e; 前言 hello hello~ &#xff0c;这里是大耳朵土土垚~&#x1f496;&#x1f496; &#xff0c;欢迎大家点赞&#x1f973;&#x1f973;关注&#x1f4a5;&#x1f4a5;收藏&#x1f339;&#x1f339;&#x1f339; &#x1f4a5;个人主页&#x…
阅读更多...
揭秘五力模型：轻松掌控企业竞争命脉，决策不再迷茫！

揭秘五力模型：轻松掌控企业竞争命脉，决策不再迷茫！

五力分析模型又成为波特五力模型是由著名的管理学者迈克尔波特(Michael Porter)在20世纪80年代初提出的一种理论框架&#xff0c;它对企业营销中的战略制定产生了全球性的深远影响。这一模型被广泛应用于企业竞争战略的分析&#xff0c;可以帮助企业有效地分析企业在营销环境中…
阅读更多...
Java实验报告2

Java实验报告2

一、实验目的 本实验为Java课程的第二次实验&#xff0c;其主要目的如下&#xff1a; 理解继承和多态的概念&#xff1b; 掌握域和方法在继承中的特点&#xff1b; 掌握构造函数的继承和重载&#xff1b; 掌握this和super的用法&#xff1b; 二、实验原理 ​ 继承性是面…
阅读更多...
上市公司-动态能力数据集（2008-2022年）

上市公司-动态能力数据集（2008-2022年）

01、数据介绍 上市公司动态能力是指企业在不断变化的外部环境中&#xff0c;通过整合、创建和重构内外部资源&#xff0c;寻求和利用机会的能力。这种能力有助于企业重新构建、调配和使用其核心竞争力&#xff0c;从而保持与时俱进&#xff0c;应对市场挑战。具体来说&#xf…
阅读更多...
Chrome DevTools中的骚操作

Chrome DevTools中的骚操作

今天来分享 Chrome DevTools 中一些非常实用的功能和调试技巧&#xff01; 保留日志 当我们刷新完页面之后&#xff0c;通常控制台的 Console 面板就会被清空。如果想保留控制台的日志&#xff0c;就可以在设置中勾选 Preserve log 选项以保留控制台中的日志。 代码覆盖率 我…
阅读更多...
快讯！TiDB v8 发版！超硬核 v8 引擎！

快讯！TiDB v8 发版！超硬核 v8 引擎！

TiDB 是 PingCAP 公司自主设计、研发的开源分布式关系型数据库&#xff0c;是一款同时支持在线事务处理与在线分析处理 (Hybrid Transactional and Analytical Processing, HTAP) 的融合型分布式数据库产品。 具备水平扩容或者缩容、金融级高可用、实时 HTAP、云原生的分布式数…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023