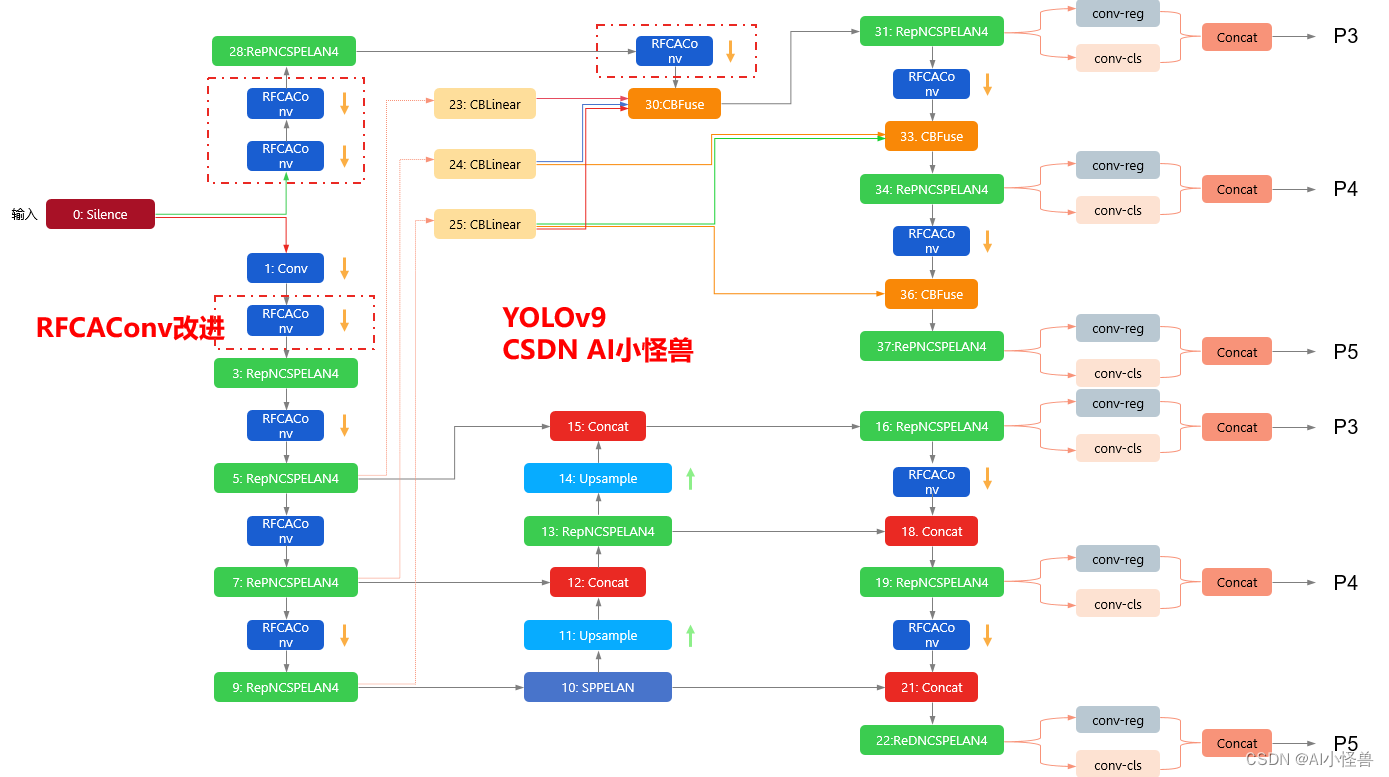
树形DP涉及到图存储，先复习一下链式前向星存储图，便于理解上篇的树形DP。对于图数据结构的存储，我们除了采用邻接矩阵（消耗空间，不常用）、邻接表，还有一种方法就是链式前向星。
链式前向星存储图结构时，需要定义头结点数组和边结点数组。

struct node{
    int to,next;
}edge[max_edge_nums];//边集数组，边数一般要设置比maxn*maxn大的数，如果题目有要求除外

int head[max_node_nums];//头结点数组

头结点数组内存放图上所有结点的编号；边结点数组中存放边终点的编号和下一条边的编号（下一条边与当前边共起点，但不共终点）。
程序设计中的输入多为边集合，即给定多组(起点，终点)的有序数对。
比如给定：
0，2
4，0
0，3
1，2
3，4
0，1
4，2
我们可以依次画出对应的有向图，有向线段的次序（即第几条有向边）也用序号标出。

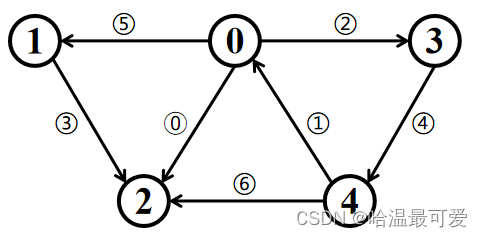
与邻接表很相似，链式前向星也开辟一块数组空间head，数组大小为拓补图中结点个数，上图中有0~4号节点，所以数组大小为5，数组内存储边的序号，数组中所有元素均初始化为-1（因为没有第-1条边，边序号从0开始）。

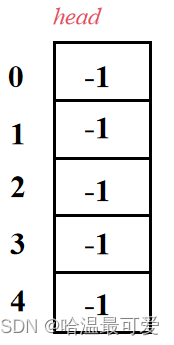
当输入第 0 条边
0，2
表示以 0 号结点为起点往外发第 0 条边，终点为 2 号结点。
效果如下：

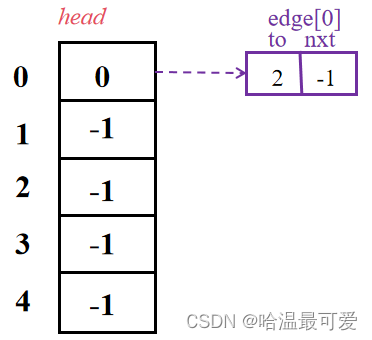
与单链表插入结点类似，先给edge[0]结点的值域内存入 to 和 nxt 值，nxt值继承 head[0] ，再修改head[0]。这里，head[i] edge[i].to 和 edge[i].nxt内存放的都是边结点数组的下标。

当输入第 1条边
4，0
效果如下：

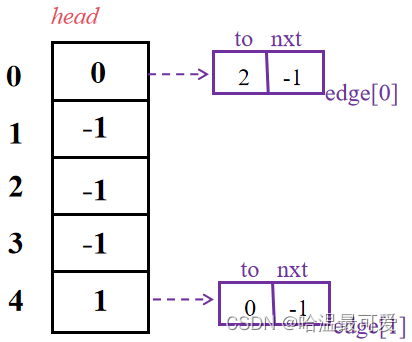
当输入第 2 条边
0，3
效果如下：

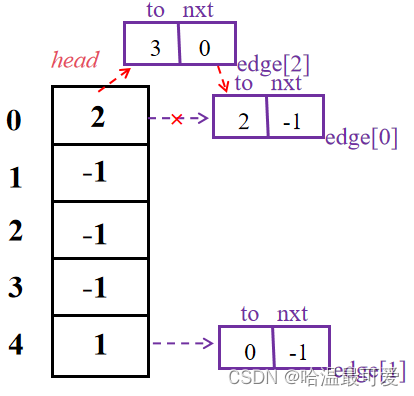
这里与单链表头插法类似，先填充 edge[2] 的终点（即第二条边指向的终点）和下一条边编号（继承 head[0] 内值），然后修改 head[0] 内值，使得以 0 为起点的第一条边是 2 号边，而非初始的 0 号边。如此第 0 号边便是第 2 号边共起点的下一条边。
输入接下来四条边，均采用头插法，得到了邻接表结构。

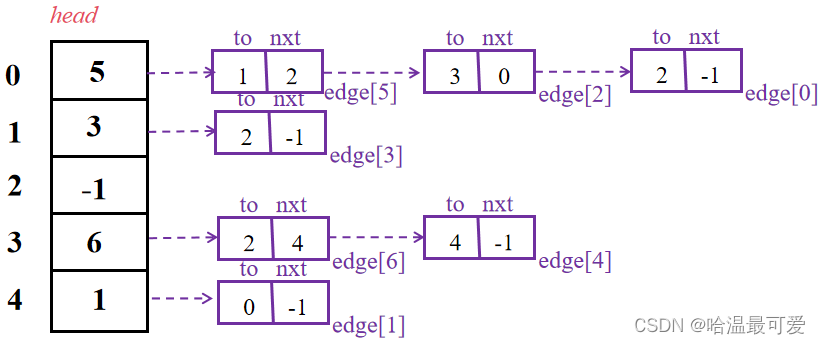
添加一条边代码如下

void add(int u,int v)
{   // 添加一条边，idx初始为0，从第 0 条边开始添加
    edge[idx].to=v; 
    edge[idx].next=head[u];
    
    // 修改头结点指向的下一条边，头插
    head[u]=cnt++;
}