题目描述：

序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时，我们可以记录下这个节点的值。如果它是一个空节点，我们可以使用一个标记值记录，例如 #。

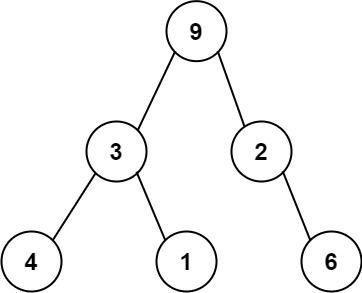
例如，上面的二叉树可以被序列化为字符串 “9,3,4,#,#,1,#,#,2,#,6,#,#”，其中 # 代表一个空节点。

给定一串以逗号分隔的序列，验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。

保证 每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 ‘#’ 。

你可以认为输入格式总是有效的

例如它永远不会包含两个连续的逗号，比如 “1,3” 。
注意：不允许重建树。

示例 1:

输入: preorder = “9,3,4,#,#,1,#,#,2,#,6,#,#”
输出: true
示例 2:

输入: preorder = “1,#”
输出: false
示例 3:

输入: preorder = “9,#,#,1”
输出: false

提示:

1 <= preorder.length <= 10⁴
preorder 由以逗号 “，” 分隔的 [0,100] 范围内的整数和 “#” 组成

解题思路一：看提示主要是栈和树。这题其实不是二叉树的遍历题，而是检验二叉树基础知识的题，也许有些难想。第一种解法是：把有效的叶子节点使用 “#” 代替。 比如把 4## 替换成 # 。此时，叶子节点会变成空节点！如此循环，最终根节点应该也是一个空节点。以此可以判断二叉树的前序序列化。

class Solution:
    def isValidSerialization(self, preorder: str) -> bool:
        stack = []
        for p in preorder.split(','):
            stack.append(p)
            while len(stack) >= 3 and stack[-1] == '#' and stack[-2] == '#' and stack[-3] != '#':
                stack.pop(), stack.pop(), stack.pop()
                stack.append('#')
        return len(stack) == 1 and stack[-1] == '#'

时间复杂度：O(n)
空间复杂度：O(n)

解题思路二：计算入度出度，仅需知道两个关键点：1. 在遍历到任何一个节点的时候，要求diff >= 0，原因是还没遍历到该节点的子节点，所以此时的出度应该大于等于入度。2. 当所有节点遍历完成之后，整棵树的 diff == 0 。

1. 每个空节点（ “#” ）会提供 0 个出度和 1 个入度。
2. 每个非空节点会提供 2 个出度和 1 个入度（根节点的入度是 0）。
3. 这里解释一下为什么下面的代码中 diff 的初始化为 1。因为，我们加入一个非空节点时，都会对 diff 先减去 1（入度），再加上 2（出度）。但是由于根节点没有父节点，所以其入度为 0，出度为 2。因此 diff 初始化为 1，是为了在加入根节点的时候，diff 先减去 1（入度），再加上 2（出度），此时 diff 正好应该是2.

class Solution:
    def isValidSerialization(self, preorder: str) -> bool:
        nodes = preorder.split(',')
        diff = 1
        for node in nodes:
            diff -= 1
            if diff < 0:
                return False
            if node != '#':
                diff += 2
        return diff == 0 

时间复杂度：O(n)
空间复杂度：O(1)

解题思路三：0

时间复杂度：O(n)
空间复杂度：O(n)