题目列表
3090. 每个字符最多出现两次的最长子字符串
3091. 执行操作使数据元素之和大于等于 K
3092. 最高频率的 ID
3093. 最长公共后缀查询
一、每个字符最多出现两次的最长子字符串

非常经典的滑动窗口问题,即动态维护一段区间,使得这段区间满足题目要求,代码如下
class Solution {
public:
int maximumLengthSubstring(string s) {
int cnt[26] = { 0 };
int n = s.size();
int ans = 0;
for(int l = 0, r = 0; r < n; r++){
cnt[s[r]-'a']++;
while(cnt[s[r]-'a']>2){
cnt[s[l]-'a']--;
l++;
}
ans = max(r-l+1,ans);
}
return ans;
}
};二、执行操作使数据元素之和大于等于K

题目中有 将元素+1 和 复制元素 两个操作。我们先来想想这两个操作哪个先执行,结果会更优?很显然,先+1再x2得到的结果 比 先x2再+1得到的结果 更大,即我们应该优先进行+1操作,然后开始复制得到的数最大,但是我们要加到多大再进行复制需要的操作次数才最小呢?我们可以暴力枚举出所有情况,然后取得最大值,代码如下
class Solution {
public:
int minOperations(int k) {
int ans = INT_MAX;
for(int i=1;i<=k;i++){
// 进行 i-1 次 +1操作
// 再进行 ceil((k-i)/i) (ceil---向上取整) 次 复制操作
ans=min(ans,i-1+(k-i+i-1)/i);
}
return ans;
}
};那有没有更加优雅的做法呢?
我们来看看i-1+(k-1)/i这个表达式,用x替换成i,得到 f(x) = x-1+(k-1)/x,问如何取f(x)的最小值?这个高中都学过,对勾函数,当x=sqrt(k-1)时,f(x)最小(如果不知道对勾函数,对它进行求导找最小值也是可以的)这里我们的x要取整数。代码如下
class Solution {
public:
int minOperations(int k) {
// 进行 x-1 次 +1操作
// 再进行 ceil((k-x)/x) (ceil---向上取整) 次 复制操作
// f(x) = x-1+(k-x+x-1)/x = x-1+(k-1)/x
if(k==1) return 0; // 分母不能为零,要特判
int x = sqrt(k-1);
if(x*x==k-1) return x*2-1;
else return min(x-1+(k-1)/x,x+1-1+(k-1)/(x+1));
}
};三、最高频率的ID

本题就是要求我们在统计ID出现次数的基础上维护出现频率的最大值 ,统计ID出现次数很简单,我们可以用哈希表存储,关键是如何维护出现频率的最大值,可以用multiset来帮助我们维护最大值,代码如下
// 哈希表 + multiset
class Solution {
public:
vector<long long> mostFrequentIDs(vector<int>& nums, vector<int>& freq) {
int n = nums.size();
vector<long long> ans(n);
multiset<long long> s;
unordered_map<int,long long> mp;
for(int i = 0; i < n; i++){
int x = nums[i];
auto it = s.find(mp[x]);
if(it != s.end())
s.erase(it);
mp[x]+=freq[i];
s.insert(mp[x]);
ans[i]=*s.rbegin();
}
return ans;
}
};
// 哈希表 + 堆(懒删除) --- 可以了解一下
// 懒删除:当我们要取出堆顶元素的时候,看它的ID和freq是否匹配,
// 如果不匹配说明已经被修改,该数据无效 pop,如果相同,则是答案
class Solution {
public:
vector<long long> mostFrequentIDs(vector<int>& nums, vector<int>& freq) {
int n = nums.size();
vector<long long>ans(n);
priority_queue<pair<long long,int>> pq;//大堆<freq,ID>
unordered_map<int,long long>mp;
for(int i=0;i<n;i++){
mp[nums[i]] += freq[i];
pq.emplace(mp[nums[i]],nums[i]);
while(pq.top().first!=mp[pq.top().second])
pq.pop();
ans[i]=pq.top().first;
}
return ans;
}
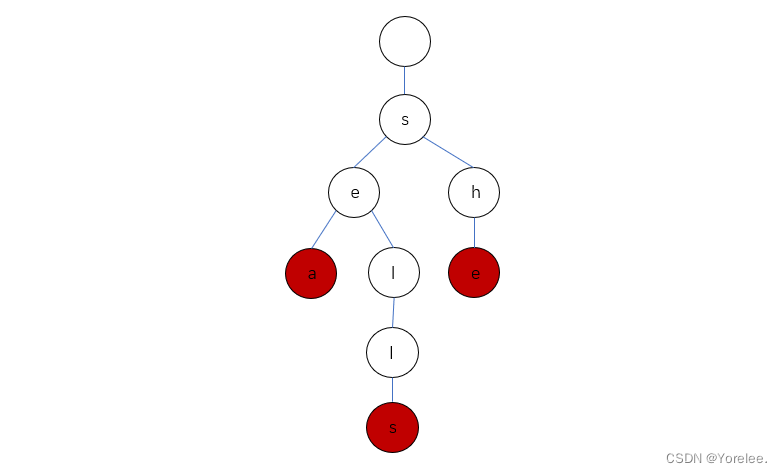
};四、最长公共后缀查询

这题没啥可说的,之前周赛出过类似的,用字典树来做
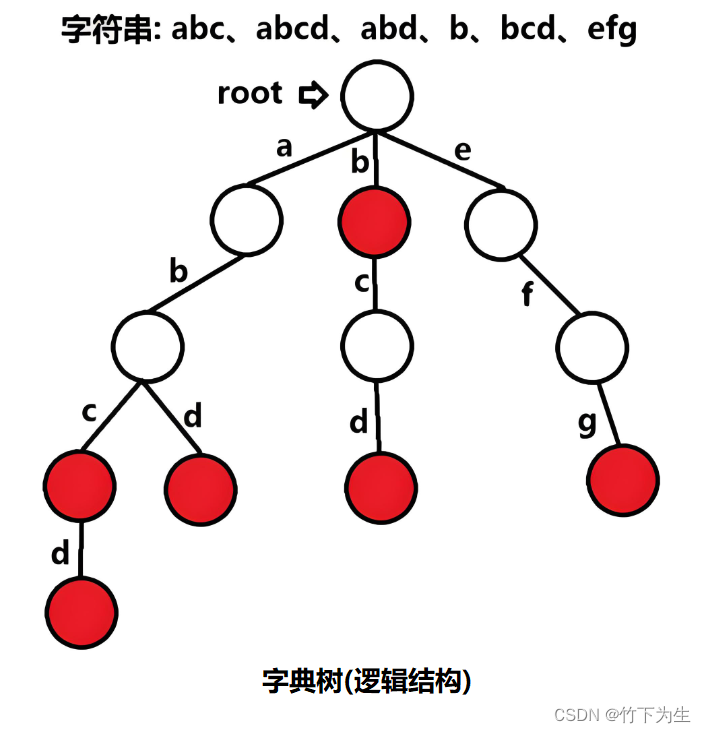
代码如下
struct Node{
Node* child[26]={0};
int idx = -1;// 记录当前后缀下长度最短的字符串下标
};
class Solution {
public:
vector<int> stringIndices(vector<string>& wordsContainer, vector<string>& wordsQuery) {
// 建立字典树
int pos = -1, mn = INT_MAX;
Node*root = new Node;
for(int i = 0; i < wordsContainer.size(); i++){
const string &s = wordsContainer[i];
int n = s.size();
if(mn > n) pos = i, mn = n; // 找最短的字符串下标
Node* cur = root;
for(int j = n-1; j >= 0; j--){
int x = s[j] - 'a';
if(cur->child[x] == nullptr)
cur->child[x] = new Node;
cur = cur->child[x];
if(cur->idx == -1 || wordsContainer[cur->idx].size() > n)
cur->idx = i;
}
}
// 查询
int m = wordsQuery.size();
vector<int> ans(wordsQuery.size(),-1);
for(int i = 0; i < m; i++){
const string &s = wordsQuery[i];
int n = s.size();
Node* cur = root;
for(int j = n-1; j >= 0; j--){
int x = s[j] - 'a';
cur = cur->child[x];
if(cur) ans[i] = cur->idx;
else break;
}
if(ans[i] == -1) ans[i] = pos;
}
return ans;
}
};