一、介绍Trie

  Trie 又称字典树、前缀树和单词查找树，如果关键词是数字序列，则称数字查找树，是一颗非典型的多叉树模型，即每个结点的分支数量可能为多个。Trie这个名字取自“retrieval”，检索，读音和 try 相同。
  百度百科：Trie

1.1、Trie的结点结构

Trie的结点结构是这样的:

strcut TrieNode{
	bool isEnd;//该结点是否是一个串的结束。
	TrieNode * next[26];//字母映射表，结点个数跟一个串中包含的字符种树有关
	TrieNode(){//默认为空
		isEnd=false;//默认不是一个串的结束
		for(auto & i:next) i=nullptr;
	}
};

  需要注意的是，一个节点即使标记为某个串的结束（isEnd=true），也可以是其他更长串的前缀。这意味着，该节点可以有子节点，它们代表着以当前串为前缀的其他串。这个特性使得Trie成为一种极其有效的数据结构，用于处理具有共同前缀的字符串集合。

1.2、Trie的整体结构

在这个结点结构下，包含三个单词 “sea”,“sells”,“she” 的 Trie 会长啥样呢？

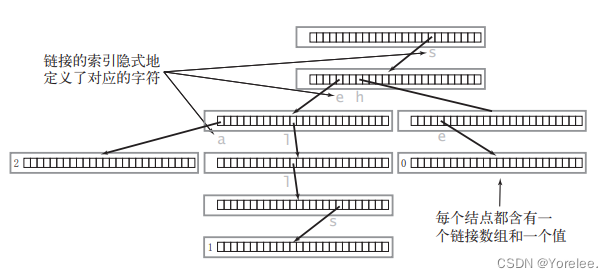
为了方便理解我们可以画成这样（也是实际树结构）：

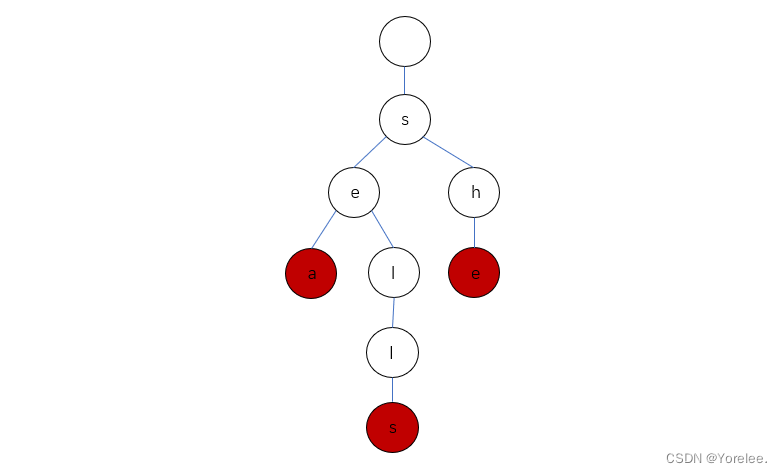
  根据整体结构，我们可以理解Trie实际上用边表示字符，每次选择一个子节点就可以选定一个字符，如果某结点对应位置为空，则说明Trie不包含 从根到该结点的边连接成的串加上该位置对应的字符 构成的 前缀。

二、Trie的操作

首先创建根结点，初始时根结点为空。

TrieNode * root=new TrieNode();

2.1、Trie插入操作

向字典树Trie中插入一个单词word，它保证使用了已有字典树的最长单词前缀：

1. 初始化：从Trie的根节点开始。
2. 遍历单词中的每个字符：对于单词 word 中的每个字符 c：
   • 检查当前节点是否存在字符 c 对应的子节点。
   • 如果存在，移动到该子节点，继续查找下一个字符。
   • 如果不存在，查找则创建该子节点，并移动到该子节点。
3. 检查单词完全匹配：在成功遍历单词 word 中的所有字符后，将最后一个节点标记isEnd=true。

void insert(string word){
	TrieNode * node=root;
	for(char c:word){
		if(node->next[c-'a']==nullptr){
			node->next[c-'a']=new TrieNode();
		}
		node=node->next[c-'a'];
	}
	node->isEnd=true;//串的结束只跟插入时的串有关。
	return;
}

2.2、Trie查找操作

判断字典树Trie中是否包含单词word：

1. 初始化：从Trie的根节点开始。
2. 遍历单词中的每个字符：对于单词 word 中的每个字符 c：
   • 检查当前节点是否存在字符 c 对应的子节点。
   • 如果存在，移动到该子节点，继续查找下一个字符。
   • 如果不存在，查找失败，返回 false（表示Trie中不存在单词 word）。
3. 检查单词完全匹配：在成功遍历单词 word 中的所有字符后，需要检查当前节点是否标记为某个单词的结尾。
   • 如果当前节点标记为单词的结尾，则查找成功，返回 true。
   • 如果当前节点未标记为单词的结尾，则意味着Trie中没有完全匹配的单词，返回 false。

bool search(string word){
	TrieNode * node=root;
	for(char c:word){
		if(node->next[c-'a']==nullptr)
			return false;
		node=node->next[c-'a'];
	}
	return node->isEnd;//if(node->isEnd) return true;
}

2.3、Trie前缀匹配操作

判断字典树Trie中是否有以prefix为前缀的单词，由于Trie是通过插入结点生成的，因此只要一颗Trie能遍历完所有prefix中的字符，那么它必然是含有以prefix为前缀的单词的。它的实现和search操作类似：

1. 初始化：从Trie的根节点开始。
2. 遍历单词中的每个字符：对于单词 prefix 中的每个字符 c：
   • 检查当前节点是否存在字符 c 对应的子节点。
   • 如果存在，移动到该子节点，继续查找下一个字符。
   • 如果不存在，查找失败，返回 false。
3. 检查单词完全匹配：在成功遍历单词 prefix 中的所有字符后，即所有字符均匹配，因此存在这样的前缀，返回true。

bool startsWith(string prefix){
	TrieNode * node=root;
	for(char c:prefix){
		if(node->next[c-'a']==nullptr)
			return false;
		node=node->next[c-'a'];
	}
	return true;
}

2.4、Trie删除操作

从Trie中删除一个串word时，我们应当从根结点把该路径上的结点依次删除，直至某结点的儿子不为空 或者 为根结点时，则不再删除。如果采用删除操作可以在树结点中记录儿子个数，这样可以快速判断是否还有儿子。可以通过在Trie结构中加入char ch，表示当前结点的字符应当是什么，可以快速找到儿子位置。这里采用整个文章的结构，所以不记录。

1. 初始化节点数组：为了存储删除路径上的每个节点，函数首先创建了一个指针数组 path，大小为待删除字符串 str 的长度。
2. 遍历Trie以找到字符串：函数遍历Trie以寻找与 str 匹配的字符串，同时在 path 数组中记录遍历过程中访问的每个节点。
3. 检查并删除字符串：
   • 如果未找到完全匹配的字符串（即在Trie中不存在该字符串），函数返回 false。
     找到后，标记其isEnd=true。从字符串的末尾开始向上回溯，检查每个节点是否有其他子节点。
   • 如果有其他子节点或该节点为根，说明当前节点是其他字符串的前缀，函数结束，返回 true。
   • 如果没有其他子节点，并且isEnd==true，则函数结束，返回true。
   • 如果没有其他子节点，并且isEnd!=true，删除当前节点，并将其父节点中对应的指针设置为 nullptr。

bool delete(string word){
	vector<TrieNode *> path;
	TrieNode * node=root;
	path.push_back(node);
	for(auto &c:word){
		if(node->next[c-'a']==nullptr)
			return false;
		node=node->next[c-'a'];
		path.push_back(node);
	}
	if(path.back()->isEnd==false) return false;
	path.back()->isEnd=false;//可能非叶子结点，不能直接删除，先标记为不是串的结尾
	bool flag=true;
	while(flag&&path.size()>1){//回溯向上，判断是否删除结点
		if(path.back()->isEnd) break;//如果是串的结尾 那么也不能再删除了
		TrieNode * child=path.back();
		for(auto &i=child->next){//查看其是否有儿子，可以通过为每一个Trie结点维护一个儿子数量，来快速判断。
			if(i!=nullptr) {flag=false;break;}//不可删除
		}
		if(flag){//没儿子
			path.pop_back();
			TrieNode * fa=path.back();
			for(auto & i=fa->next)//找到儿子，并删除，可以通过在Trie结构中加入char ch，表示当前结点的字符应当是什么，可以快速找到儿子位置。
				if(i==child) {delete child;i=nullptr;break;}//删了之后break;不break会访问野指针。~
		}
	}
	return true;
}

这里需要注意指针 和 指针指向的内容 的区别：

• i==child：指的是i和child的值相同，指针类型 相当于i和child指向的地址相同。
• delete child：指的是回收child指向的内容。
• i=nullptr：i是引用，实际上是修改i引用的fa->next[x]=nullptr。

三、实战

3.1、实现Trie（前缀树）

题目链接：LeetCode：208.实现Trie（前缀树）

class Trie {
public:
    Trie() {
        isEnd=false;
        for(auto &i:next) i=nullptr;
    }
    
    void insert(string word) {
        Trie * node=this;//this指针表示被插入的字典树的根结点。
        for(char c:word){
            if(node->next[c-'a']==nullptr)
                node->next[c-'a']=new Trie();
            node=node->next[c-'a'];
        }
        node->isEnd=true;
        return;
    }
    
    bool search(string word) {
        Trie * node=this;
        for(char c:word){
            if(node->next[c-'a']==nullptr)  return false;
            node=node->next[c-'a'];
        }
        return node->isEnd;
    }
    
    bool startsWith(string prefix) {
        Trie * node=this;
        for(char c:prefix){
            if(node->next[c-'a']==nullptr)  return false;
            node=node->next[c-'a'];
        }
        return true;
    }
private:
    bool isEnd;
    Trie * next[26];
};
/*使用样例：始终对root进行插入、查找、前缀匹配查找操作
Trie * root=new Trie;
root->insert(val);
root->insert(val2);
root->insert(val3);
if(root->search(val4)) cout<<true<<endl;
if(root->startsWith(val4)) cout<<true<<endl;
*/