目录

题目

思路

代码

---

先来说下什么时候使用贪心和动态规划：

        一个题目当寻找答案的过程中有大约 2的指数级（ 2^n）个方案的时候，可以考虑用贪心和动态规划问题（其实，我现在还不知道什么时候用 dfs 和 动态规划，希望有大佬教教我）。

        当这 2^n 个路径中有多个方案可能指向最优解的时候，用动态规划。

        当这 2^n 个路径中只有某一个方案指向最优解的时候，用贪心。

        大概解释意思就是：

        当有多个方案指向最优解的时候，我们可以将一个大的问题划分为多个子问题，并使用动态规划来计算每个子问题的最优解，然后将这些最优解组合起来得到原问题的最优解。 

         当只有一条最优方案的时候，我们就用贪心，每步都使用最优策略来寻找解。

        

        贪心问题（和二分很像）：

        例如二分，每次取中间值，判断目标值和中间值的位置，然后判断取左边还是右边，但是保证目标值在所求区间范围内。

        回到贪心来说，贪心问题，如上述所说：

        类比于二分，用一个集合来表示所有路径解，我们可以将这个集合分成两类，贪心问题一般我们都可以发现其中最优解必定在其中一类中。

        然后再对有最优解的一类进行这种类似二分的方式划分，将集合缩小，缩小的集合中一定有最优解，那么当集合只有一个元素的时候，那么就是最优解。

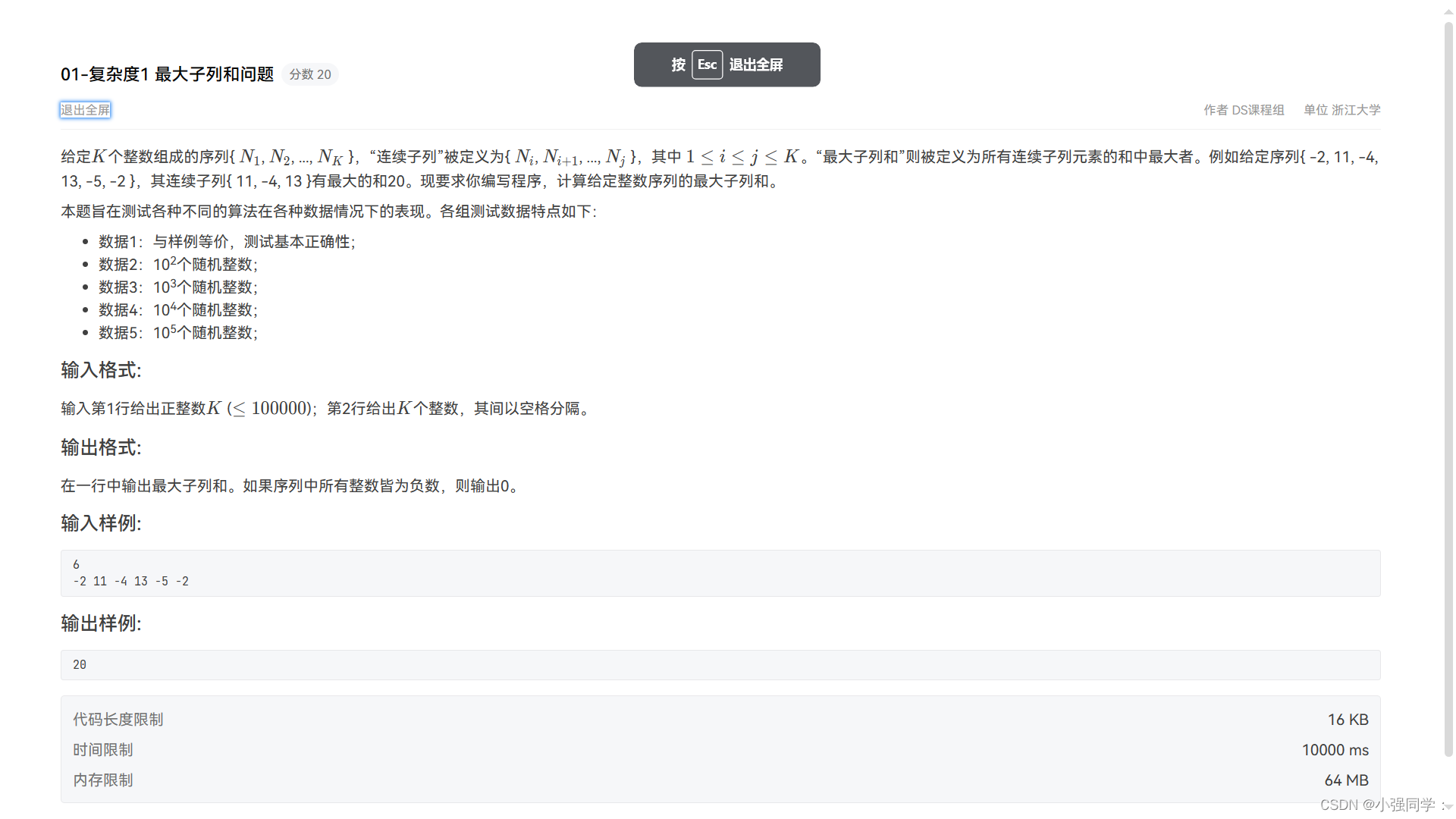
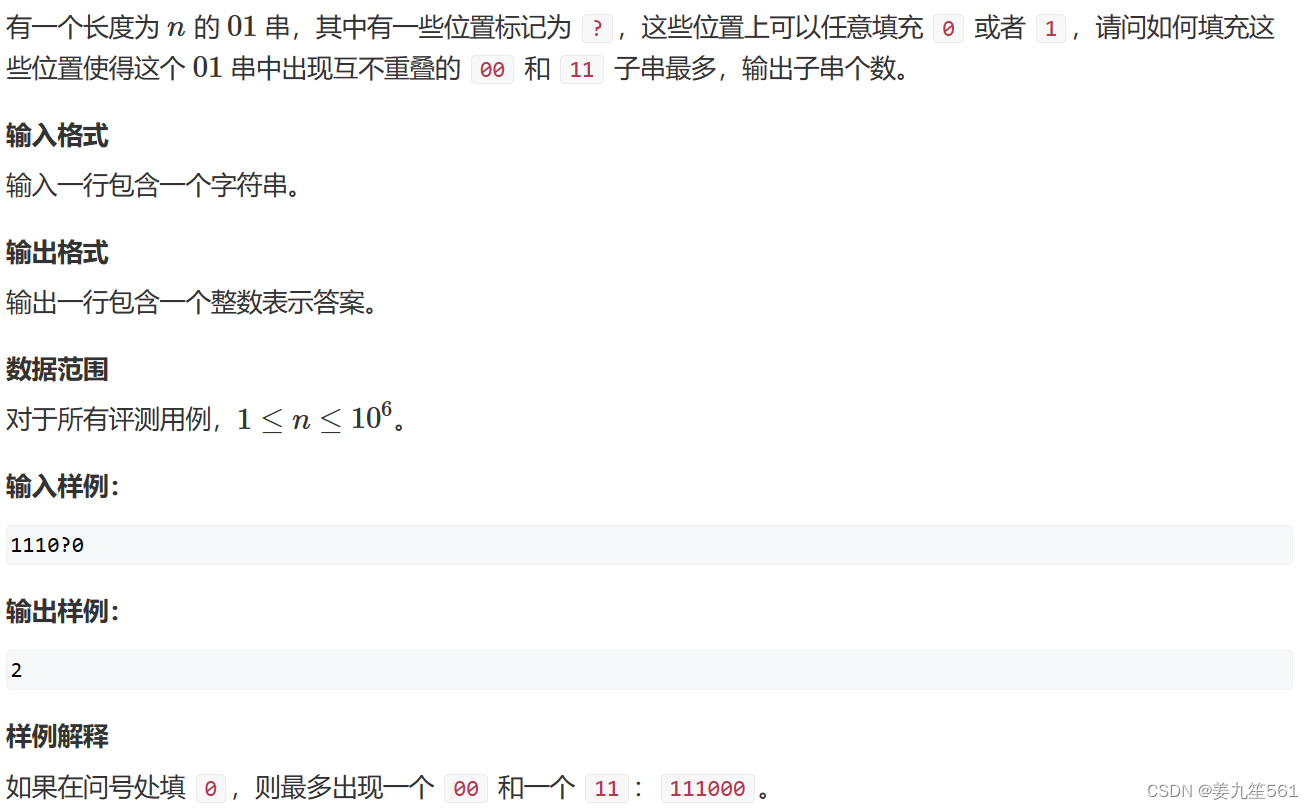
题目

思路

        从前往后枚举，如果当前点能够跟后面的一个点进行配对（即为 11, 00 , 1? , 0? , ?1 , ?0 , ??这七种情况），那么我们算一个子串，这两个点不再跟别的点进行配对，枚举到 n-1 ，就可以知道有多少个子串。是一个非常经典的贪心问题，如若想了解为什么这样，即证明过程，可以参考y总的讲解：AcWing 4966. 填充（寒假每日一题2024） - AcWing

 问就是太菜了，证明对我来说太神奇了。

代码

import java.io.*;

class Main{
    static int res;
    public static void main(String[] args) throws IOException{
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        String s = in.readLine();
        for(int i=0;i<s.length()-1;i++){
            if(s.charAt(i)==s.charAt(i+1)||s.charAt(i)=='?'||s.charAt(i+1)=='?'){
                res++;
                i++;
            }
        }
        System.out.println(res);
    }
}