第一题《求和》【简单模拟】
【问题描述】
求1(含)至20230408(含)中每个数的和。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
【代码】
#include <iostream>
using namespace std;
int main()
{
long long res = 0;
for(int i = 1;i<=20230408;i++) res += i;
printf("%lld",res);
// 请在此输入您的代码
return 0;
}【答案】
204634714038436
第二题《工作时长》【模拟】
【问题描述】

【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
【代码】
#include <bits/stdc++.h>
using namespace std;
//2022是平年
int Month[13] = {0, 31, 59, 90, 120, 151, 181, 212, 243, 273, 304, 334, 365};
int sum[520];
int month, day, h, mi, s; //月,日,时,分,秒
int main() {
int ans = 0;
for (int i = 0; i < 520; i++) {
string str;
getline(cin, str);
month = (str[6] - '0') + (str[5] - '0') * 10;
day = (str[9] - '0') + (str[8] - '0') * 10;
h = (str[12] - '0') + (str[11] - '0') * 10;
mi = (str[15] - '0') + (str[14] - '0') * 10;
s = (str[18] - '0') + (str[17] - '0') * 10;
sum[i] = (Month[month - 1] + day) * 86400 + h * 3600 + mi * 60 + s;
}
sort(sum, sum + 520);
for (int i = 0; i < 520; i += 2) {
ans += sum[i + 1] - sum[i];
}
cout << ans << endl;
return 0;
}【答案】
5101913
第三题《三国游戏》【贪心】
本题题解参考这篇博客:【贪心】第十四届蓝桥杯省赛C++ / Java / Python C组《三国游戏》(C++)
第四题《填充》【贪心】
本题题解参考这篇博客:【贪心】第十四届蓝桥杯省赛C++ / Java / Python C组《填充》(C++)
第五题 《翻转》【思维】
本题题解参考这篇博客:【思维】第十四届蓝桥杯省赛C++ C组/研究生组 Python A组/C组《翻转》(C++)
第六题《子矩阵》【单调队列】
本题题解参考这篇博客:【单调队列】第十四届蓝桥杯省赛C++ C组 Java C组/研究生组 Python A组《子矩阵》(C++)
第七题《互质数的个数》【欧拉函数+快速幂】
本题题解参考这篇博客:【欧拉函数+快速幂】第十四届蓝桥杯省赛C++ C组 Java A组/研究生组 Python 研究生组《互质数的个数》(C++)
第八题《异或和之差》【trie树】
【题目描述】
给定一个含有 n 个元素的数组 ,你可以选择两个不相交的子段。
求出这两个子段内的数的异或和的差值的最大值。
【输入格式】
输入的第一行包含一个整数 n。
第二行包含 n 个整数 ,相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【数据范围】
对于 40% 的评测用例,n ≤ 5000;
对于所有评测用例,2 ≤ n ≤ 2×,0 ≤
≤
。
【输入样例】
6
1 2 4 9 2 7
【输出样例】
14
【样例解释】
两个子段可以分别选 1 和 4,9,2,差值为 15−1=14。
【思路】
求异或最值,一般用trie树做。
trie树可以在len(num)的时间内求出与num异或最大/最小的值
题目求的是区间,我们可以维护一个前缀异或和sum[i],那么我们求一段异或和最大,也就是求前缀和中的与sum[i]异或最大的值,最小同理,
题目求的是两段区间的差值最大,因为两段区间不相交,我们可以先求出前缀的最大/最小值,后缀在求一遍,答案就是前缀最大值-后缀最小值 or 后缀最大值-前缀最小值
【代码】
#include <bits/stdc++.h>
using namespace std ;
typedef long long LL ;
typedef pair<LL,int> PLI ;
const int N = 1e6 + 10 ;
int n , a[N] ;
int son[2][N] , idx ;
int mx[N] , mi[N] ;
void insert(int x)
{
int p = 0 ;
for(int i = 20 ; i >= 0 ; i --)
{
int u = (x >> i) & 1 ;
if(!son[u][p]) son[u][p] = ++ idx ;
p = son[u][p] ;
}
}
int query_mi(int x)
{
int p = 0 , res = 0;
for(int i = 20 ; i >= 0 ; i --)
{
int u = (x >> i) & 1 ;
if(!son[u][p])
{
u = !u ;
res |= (1 << i) ;
}
p = son[u][p] ;
}
return res ;
}
int query_mx(int x)
{
int p = 0 , res = 0;
for(int i = 20 ; i >= 0 ; i --)
{
int u = (x >> i) & 1 ;
if(son[!u][p]) res |= (1 << i) ;
else u = !u ;
p = son[!u][p] ;
}
return res ;
}
int main()
{
cin >> n ;
for(int i = 1 ; i <= n; i ++) cin >> a[i] ;
mx[0] = 0 , mi[0] = 2e9 ;
int sum = 0 ;
insert(sum) ;
for(int i = 1 ; i <= n ; i ++)
{
sum ^= a[i] ;
mx[i] = max(mx[i - 1] , query_mx(sum)) ;
mi[i] = min(mi[i - 1] , query_mi(sum)) ;
insert(sum) ;
}
memset(son , 0 , sizeof son) ;
idx = 0 ; sum = 0 ;
int ans = 0 , mx2 = 0 , mi2 = 2e9;
insert(sum) ;
for(int i = n ; i ; i --)
{
sum ^= a[i] ;
mx2 = max(mx2 , query_mx(sum)) ;
mi2 = min(mi2 , query_mi(sum)) ;
ans = max({ans , mx[i - 1] - mi2 , mx2 - mi[i - 1]}) ;
insert(sum) ;
}
cout << ans << endl ;
return 0 ;
}第九题《公因数匹配》【质因数分解】
【题目描述】
给定 n 个正整数 ,请找出两个数 i,j 使得 i<j 且
和
存在大于 1 的公因数。
如果存在多组 i,j,请输出 i 最小的那组。
如果仍然存在多组 i,j,请输出 i 最小的所有方案中 j 最小的那组。
【输入格式】
输入的第一行包含一个整数 n。
第二行包含 n 个整数分别表示 ,
,⋅⋅⋅,
,相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含两个整数分别表示题目要求的 i,j,用一个空格分隔。
由于官方没有提及无解时如何进行输出,所以本题目前保证有解。
【数据范围】
对于 40% 的评测用例,n≤5000;
对于所有评测用例,1≤n≤,1≤Ai≤
。
【输入样例】
5
5 3 2 6 9
【输出样例】
2 4
【代码】
#include <iostream>
#include <algorithm>
#include <vector>
#define x first // 宏定义,方便使用pair中的两个元素
#define y second
using namespace std;
typedef pair<int, int> PII; // 定义pair类型,用于存放下标
const int N = 1e6 + 10;
int n;
int a[N]; // a数组用于存放每个质因子在数列中最后一次出现的位置
vector<PII> v; // 存放有重叠的两个数的下标
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++)
{
int x;
scanf("%d", &x);
// 对x进行质因数分解
for (int j = 2; j <= x / j; j ++)
{
if (x % j == 0)
{
// 如果j已经在数列中出现过了,说明有至少一个数和当前数在j这个质因子上有重叠
if (a[j]) v.push_back({a[j], i});
else a[j] = i; // 否则将j在a数组中标记为当前数在数列中的下标
while (x % j == 0) x /= j; // 将j从x中除掉,以便下一个质因子的分解
}
}
if (x > 1)
{
// 如果x剩下了一个大于1的质因子,同上处理
if (a[x]) v.push_back({a[x], i});
else a[x] = i;
}
}
sort(v.begin(), v.end()); // 按照第一个元素(之前标记的下标)排序
printf("%d %d", v[0].x, v[0].y); // 输出第一个元素即可
return 0;
}第十题《子树的大小》【模拟】
【题目描述】

【输入格式】
输入包含多组询问。
输入的第一行包含一个整数 T,表示询问次数。
接下来 T 行,每行包含三个整数 n,m,k 表示一组询问。
【输出格式】
输出 T 行,每行包含一个整数表示对应询问的答案。
【数据范围】
对于 40% 的评测用例,T≤50,n≤,m≤16;
对于所有评测用例,1≤T≤,1≤k≤n≤
,2≤m≤
。
【输入样例】
3
1 2 1
11 3 4
74 5 3
【输出样例】
1
2
24
【思路】
题解来源:AcWing 4971. 子树的大小 - AcWing
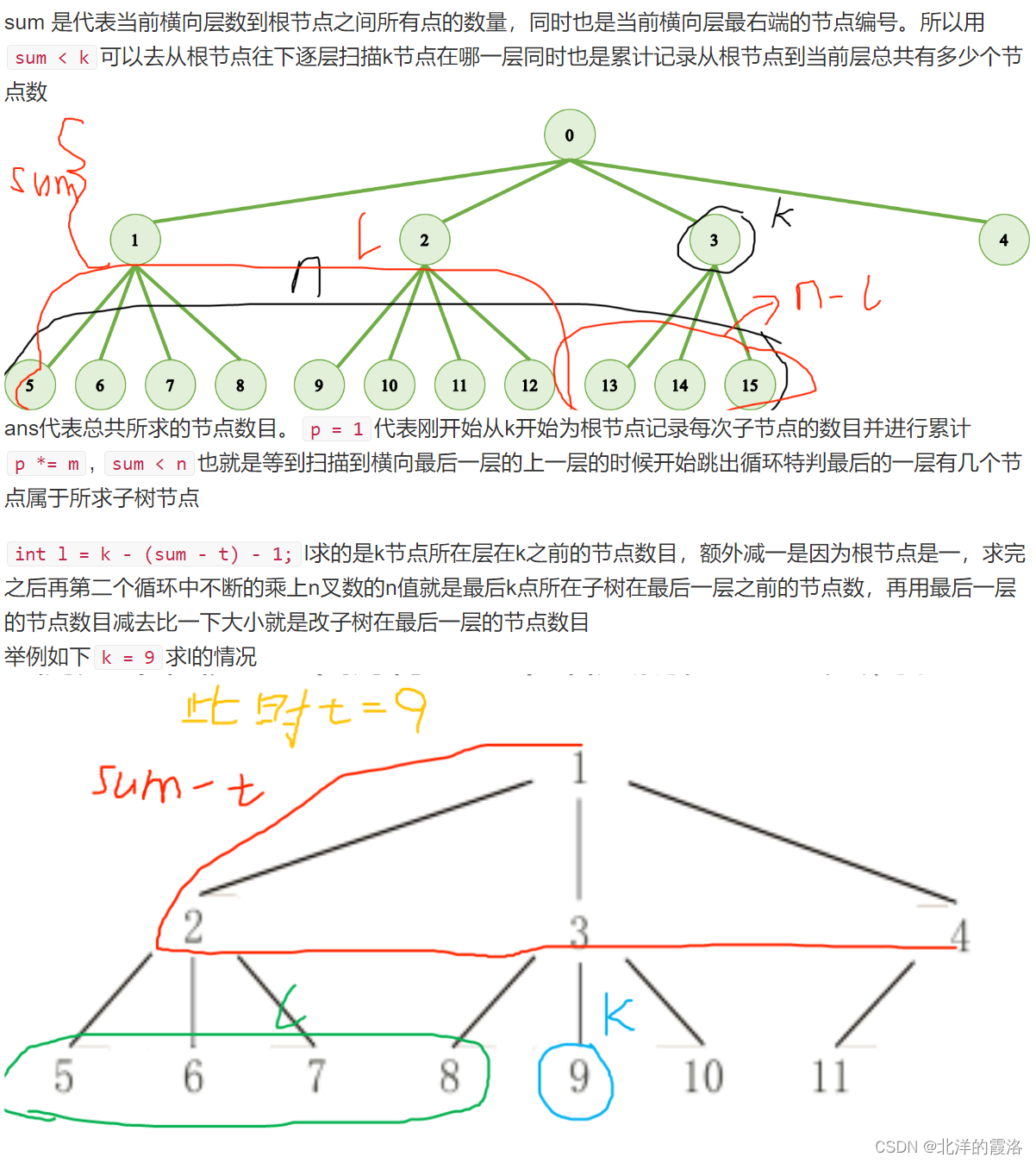
【代码】
#include<iostream>
#include<cstring>
#include<algorithm>
#define int long long
using namespace std;
typedef long long ll;
int n, m;
int k;
int sum;
signed main()
{
int T;
cin >> T;
while(T --)
{
cin >> n >> m >> k;
int t = 1;
sum = 1;
while(sum < k)
{
t *= m;
sum += t;
}
int ans = 0, p = 1;
int l = k - (sum - t) - 1;
while(sum < n)
{
ans += p;
l = l * m;
t *= m;
p *= m;
sum += t;
}
n -= sum - t;
ans += min(p, max(0ll, n - l));
cout << ans << endl;
}
return 0;
}以上内容部分题目题解摘自他人博客题解,在题目处均已标明出处。若有侵权,私信删除。