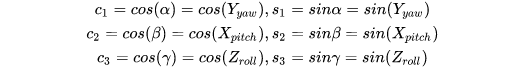目录
一、前言
二、二分法理论
1、引导:猜数游戏
2、理论背景:非线性方程的求根问题
1)非线性方程的近似解
2)搜索法和二分法
3、用二分的两个条件
4、二分法复杂度
三、整数二分
1、在单调递增序列中找 x 或者 x 的后继
2、在单调递增序列中查找 x 或者 x 的前驱
3、对比
4、分巧克力(lanqiaoOJ题号99,2017年省赛)
(1)暴力法
(2)二分法
5、跳石头(lanqiaoOJ题号364)
(1)二分法套路题:最小值最大化、最大值最小化
6、青蛙过河(lanqiaoOJ题号2097)
四、实数二分
1、一元三次方程求解
(1)暴力法
(2)二分法
五、二分法习题
一、前言
二分法相信大家或多或少都有所了解,希望下面的内容能帮助大家对二分法有更深入更系统的理解。
二、二分法理论
1、引导:猜数游戏
一个 [1, 100] 内的数字,只需猜 7 次:
>50? 是。[1, 100] 二分,中位数 50,下一步猜 [51, 100]
>75? 否。[51, 100] 二分,中位数 75,下一步猜 [51, 75]
>63? 否。[51, 75] 二分,...
>56? 否。[51, 63] 二分,
>53? 是。
>54? 否。
=54? 是。
这个数是 54
- 二分法:折半搜索
- 二分的效率:很高,O(logn)
- 例如猜数游戏,若n=1000万,只需要猜 log10^7 = 24 次
- 二分法能把一个长度为 n 的有序序列上 O(n) 的查找时间,优化到了 O(logn)
猜数游戏的代码:
def bin_search(a,n,x): #在数组a中找数字x,返回位置
left=0
right=n
while left<right:
mid=left+(right-left)//2
if a[mid]>=x:
right=mid
else:
left=mid+1
print('[',left,right,']') #打印猜数游戏的过程
return left
n=100
a=[i for i in range(1,101)] #初始化1~100
test=54
pos=bin_search(a,n,test)
print("test=",a[pos])2、理论背景:非线性方程的求根问题
- 满足方程:f(x)=0 的数 x 称为方程的根。
- 非线性方程:指 f(x) 中含有三角函数、指数函数或其他超越函数。
- 非线性方程,很难或者无法求得精确解。
- 二分法是一种求解的方法
1)非线性方程的近似解
【非线性方程】
在实际应用中,只要得到满足一定精度要求的近似解就可以了。
【根的存在性】
判定:设函数在闭区间 [a, b] 上连续,且 f(a)·f(b)<0,则 f(x) = 0 存在根。
【求根】
有两种方法:搜索法、二分法。
2)搜索法和二分法
【搜索法】
把区间 [a, b] 分成 n 等份,每个子区间长度是 Δx,计算点 xk = a + kΔx (k=0,1,2,3,4,.,n) 的函数值f(xk),若 f(xk) = 0,则是一个实根,若相邻两点满足 f(xk)·f(xk+1)<0,则在 (xk, xk+1) 内至少有一个实根,可以取 (xk+ xk+1)/2 为近似根。
【二分法】
如果确定 f(x) 在区间 [a, b] 内连续,且 f(a)·f(b)<0,则至少有一个实根。二分法的操作,就是把 [a, b] 逐次分半,检查每次分半后区间两端点函数值符号的变化,确定有根的区间。
3、用二分的两个条件
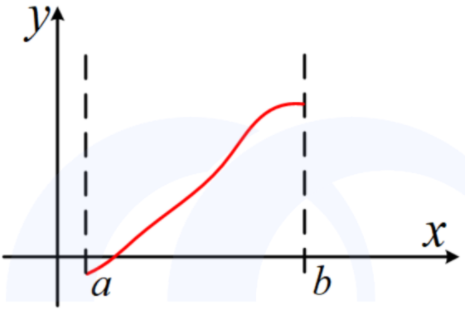
【条件】
上下界 [a, b] 确定
函数在 [a,b] 内单调。
4、二分法复杂度
- n 次二分后,区间缩小到 (b- a)/2^n。
- 给定 a、b 和精度要求 ε,可以算出二分次数 n,即满足 (b - a)/2^n < ε
- 二分法的复杂度是 O(logn) 的。
- 例如,如果函数在区间 [0,100000] 内单调变化,要求根的精度是10^-8,那么二分次数是 44 次。
三、整数二分
操作的序列中都是整数
mid = (left+right) // 2
mid = left + (right-left) // 2
1、在单调递增序列中找 x 或者 x 的后继
- 在单调递增数列 a[ ] 中查找某个数 x,如果数列中没有 x,找比它大的下一个数。
- a[mid]>=x 时:x 在 mid 的左边,新的搜索区间是左半部分,left不变,更新 right= mid。
- a[mid]<x 时:x 在 mid 的右边,新的搜索区间是半部分,right不变,更新 left=mid+1。
- 代码执行完毕后,left=right,两者相等,即答案所处的位置。
def bin_search(a,n,x): #在数组a中找数字x,返回位置
left=0
right=n #左闭右开[0,n)
while left<right:
mid=left+(right-left)//2
if a[mid]>=x:
right=mid
else:
left=mid+1
#print('[',left,right,']') #打印猜数游戏的过程
return left2、在单调递增序列中查找 x 或者 x 的前驱
- 在单调递增数列 a[ ] 中查找某个数 x,如果数列中没有 x,找比它小的前一个数。
- a[mid] <= x时,x 在 mid 的右边,新的搜索区间是右半部分,所以 right 不变,更新 left=mid;
- a[mid] > x时,x 在 mid 的左边,新的搜索区间是左半部分,所以left不变,更新 right=mid-1。
def bin_search(a,n,x): #在数组a中找数字x,返回位置
left=0
right=n #左闭右开[0,n)
while left<right:
mid=left+(right-left+1)//2
if a[mid]<=x:
right=mid
else:
left=mid-1
#print('[',left,right,']') #打印猜数游戏的过程
return left3、对比

二分的应用场景:
1)存在一个有序的数列上;
2)能够把题目建模为在有序数列上查找一个合适的数值。
4、分巧克力(lanqiaoOJ题号99,2017年省赛)
【题目描述】
有 K 位小朋友到小明家做客。小明拿出了巧克力招待小朋友们。小明一共有 N 块巧克力,其中第 i 块是 Hi × Wi 的方格组成的长方形。为了公平起见,小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。切出的巧克力需要满足:(1) 形状是正方形,边长是整数;(2) 大小相同。
例如一块 6×5 的巧克力可以切出 6块2×2 的巧克力或者 2块3X3 的巧克力。小朋友们都希望得到的巧克力尽可能大,你能帮小明计算出最大的边长是多少?
【输入描述】
第一行包含两个整数 N, K (1<=N, K<=10^5)。以下 N 行每行包含两个整数 Hi, Wi ( 1<=Hi, Wi<=10^5)。输入保证每位小朋友至少能获得一块 1×1 的巧克力。
【输出描述】
输出切出的正方形巧克力最大可能的边长。
(1)暴力法
- 把边长从 1 开始到最大边长 d,每个值都试一遍,一直试到刚好够分的最大边长为止。
- 编码:边长初始值 d=1,然后 d=2,3,4,一个个试。
复杂度:n 个长方形,长方形的最大边长 d。
check() 计算量是 O(n),做 d 次check(),总复杂度 O(n×d),n 和 d 的最大值是 10^5,超时。
def check(d): #检查够不够分
num=0
for i in range(n):
num+=(h[i]//d)*(w[i]//d)
if num>=k:
return True
else:
return False #不够分
h=[0]*100010
w=[0]*100010
n,k=map(int,input().split())
for i in range(n):
h[i],w[i]=map(int,input().split())
d=1 #正方形边长
while True:
if check(d):
d+=1 #变长从1开始,一个个地暴力试
else:
break
print(d-1)
(2)二分法
- 一个个试边长 d 太慢了,现在使用二分,按前面的“猜数游戏”的方法猜 d 的取值。
- 暴力法需要做 d 次 check(), 用二分法,只需要做 O(logd) 次 check(),总复杂度 O(nlogd)。
def check(d): #检查够不够分
num=0
for i in range(n):
num+=(h[i]//d)*(w[i]//d)
if num>=k:
return True
else:
return False #不够分
h=[0]*100010
w=[0]*100010
n,k=map(int,input().split())
for i in range(n):
h[i],w[i]=map(int,input().split())
L,R=1,100010
while L<R:
mid=(L+R)//2
if check(mid):
L=mid+1
else:
R=mid
print(L-1)
#d=1 #正方形边长
#while True:
#if check(d):
#d+=1 #变长从1开始,一个个地暴力试
#else:
# break
#print(d-1)
5、跳石头(lanqiaoOJ题号364)
【题目描述】
"跳石头"比赛在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 n 块岩石 (不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走 m 块岩石 (不能移走起点和终点的岩石)。
【输入描述】
输入文件第一行包含三个整数 L, N, M,分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。接下来 N 行,每行一个整数,第 i 行的整数 Di (0<Di<L) 表示第 i 块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同一个位置。其中,0<=M<=N<=5×10^4,1<=L<=10^9。
【输出描述】
输出只包含一个整数,即最短跳跃距离的最大值。
(1)二分法套路题:最小值最大化、最大值最小化
在 n 块岩石中移走 m 个石头,有很多种移动方法。在第 i 种移动方法中,剩下的石头之间的距离,有一个最小距离 ai。
在所有移动方法的最小距离 ai 中,问最大的 ai 是多少。在所有可能的最小值中,找最大的那个,就是 “最小值最大化”。
如果用暴力法找所有的组合,在 n 块岩石中选 m 个石头的组合情况太多,显然会超时。
转换思路,不去找搬走石头的各种组合,而是给出一个距离d,检查能不能搬走 m 块石头而得到最短距离 d。把所有的 d 都试一遍,肯定能找到一个最短的d。用二分法找这个 d 即可。
用二分法找一个最小距离 d。函数 check(d) 检查 d 这个距离是否合适。
lenn,n,m=map(int,input().split())
stone=[] #石头i和到起点的距离
def check(d):
num=0
pos=0
for i in range(0,n): #0到n-1作为石头下标
if stone[i]-pos<d:
num+=1 #第i块可以搬走
else:
pos=stone[i]
if num<=m:
return True
else:
return False
for i in range(n):
t=int(input())
stone.append(t)
L,R=0,lenn
while L<R:
mid=L+(R-L)//2
if check(mid):
L=mid+1
else:
R=mid-1
if check(L):
print(L)
else:
print(L-1)6、青蛙过河(lanqiaoOJ题号2097)
【题目描述】
小青蛙住在一条河边,它想到河对岸的学校去学习。小青蛙打算经过河里的石头跳到对岸。河里的石头排成了一条直线,小青蛙每次跳跃必须落在一块石头或者岸上。不过,每块石头有一个高度,每次小青蛙从一块石头起跳,这块石头的高度就会下降1,当石头的高度下降到 0 时小青蛙不能再跳到这块石头上 (某次跳跃后使石头高度下降到 0 是允许的)。小青蛙一共需要去学校上 x 天课,所以它需要往返 2x 次。当小青蛙具有一个跳跃能力 y 时,它能跳不超过 y 的距离。请问小青蛙的跳跃能力至少是多少才能用这些石头上完 x 次课。
【输入格式】
输入的第一行包含两个整数 n, x,分别表示河的宽度和小青蛙需要去学校的天数。请注意 2x 才是实际过河的次数。第二行包含 n-1 个非负整数 H1, H2, …… , Hn-1,其中 Hi>0 表示在河中与小青蛙的家相距的地方有一块高度为 Hi 的石头,Hi=0 表示这个位置没有石头。
【输出格式】
输出一行,包含一个整数,表示小青蛙需要的最低跳跃能力。
【样例输入】
5 1
1 0 1 0
【样例输出】
4
【样例解释】
由于只有两块高度为 1 的石头,所以往返只能各用一块。第 1 块石头和对岸的距离为 4,如果小青蛙的跳跃能力为 3 则无法满足要求。所以小青蛙最少需要 4 的跳跃能力。
【评测用例规模与约定】
对于 30% 的评测用例,n<100;对于 60% 评测用例,n<1000;对于所有评测用例,1<=n<=105, 1<=x<=109, 1<=Hi<=104。
- 往返累计 2x 次相当于单向走 2x 次。
- 跳跃能力越大,越能保证可以通过 2x 次。
- 用二分法找到一个最小的满足条件的跳跃能力。
- 设跳跃能力为 mid,每次能跳多远就跳多远,用二分法检查 mid 是否合法。
def check(mid):
for i in range(mid,n):
if sum[i]-sum[i-mid]<2*x:
return False
return True
n,x=map(int,input().split())
h=list(map(int,input().split()))
sum=[0,h[0]]
for i in range(1,len(h)):
sum.append(h[i]+sum[i])
L=0
R=100000
while L<=R:
mid=(L+R)//2
if check(mid):
R=mid-1
else:
L=mid+1
print(L)
四、实数二分
- 与整数二分法相比,实数二分容易多了,不用考虑整数的取整问题。
- 两种写法:while、for
eps=0.00001 #精度,如果用for,可以不要eps
while right-left>eps:
#for i in range(100):
mid=left+(right-left)/2
if check(mid):
right=mid #判定
else:
left=mid1、一元三次方程求解
【题目描述】
有形如:ax^3+ bx^2+ cx+ d = 0 这样的一个一元三次方程。给出该方程中各项的系数 (a,b,c,d均为实数),并约定该方程存在三个不同实根 (根的范围在 -100 至 100 之间),且根与根之差的绝对值>=1。要求由小到大依次在同一行输出这三个实根 (根与根之间留有空格),并精确到小数点后 2 位。
【输入描述】
输入一行,4 个实数 a, b, c, d。
【输出描述】
输出一行,3 个实根,从小到大输出,并精确到小数点后 2 位。
(1)暴力法
- 本题数据范围小,可以用暴力法模拟。一元三次方程有 3 个解,用暴力法,在根的范围 [-100,100] 内一个个试。答案只要求 3 个精度为 2 位小数的实数,那么只需要试 200*100 = 20000 次就行了。
- 判断一个数是解的方法:如果函数值是连续变化的,且函数值在解的两边分别是大于0和小于0,那么解就在它们中间。例如函数值 f(i) 和 f(j) 分别大于、小于0,那么解就在 [i, j] 内。
(2)二分法
- 如果题目要 “精确到小数点后 6 位”,上面的暴力法需要计算 200*106 次,超时了。
- 用二分法。题目给了一个很好的条件:根与根之差的绝对值大于等于 1。那么所有的 [i, i+1] 小区间内做二分查找就行。
def y(x):
return a*x*x*x+b*x*x+c*x+d
n=input().split()
a,b,c,d=eval(n[0]),eval(n[1]),eval(n[2]),eval(n[3])
for i in range(-100,100):
left=i
right=i+1
y1=y(left)
y2=y(right)
if y1==0:
print("{:.2f}".format(left),end=" ")
if y1*y2<0:
#while right-left>=0.001: #eps=0.001
for i in range(100): #100次二分
mid=(left+right)/2
if y(mid)*y(right)<=0:
left=mid
else:
right=mid
print("{:.2f}".format(right,end=" "))
五、二分法习题
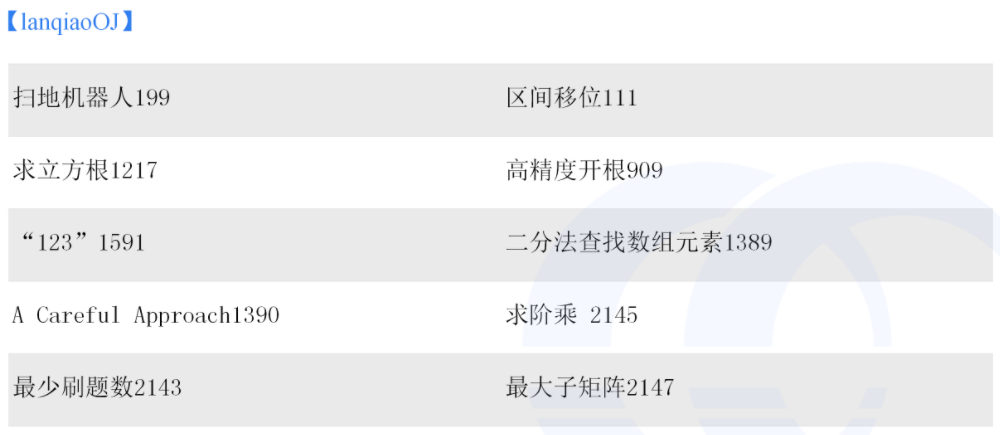
以上, 二分法讲解
祝好