目录
问题描述:
实现代码与解析:
直接模拟(递归):
原理思路:
索引版本:
问题描述:
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:
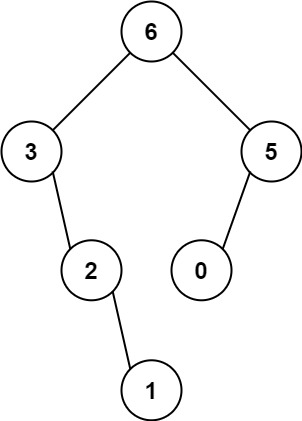
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
示例 2:
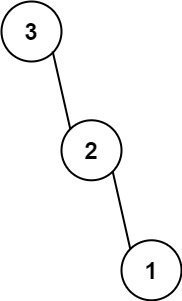
输入:nums = [3,2,1] 输出:[3,null,2,null,1]
实现代码与解析:
直接模拟(递归):
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums)
{
//数组为空
if(nums.size()==0) return NULL;
TreeNode* root=new TreeNode(nums[0]);
//叶子结点
if(nums.size()==1) return root;
int index;//切割点
int max=INT_MIN;//最大值
//找切割点
for(int i=0;i<nums.size();i++)
{
if(nums[i]>max)
{
max=nums[i];
index=i;
}
}
root->val=nums[index];
//切割数组
vector<int> leftNums(nums.begin(),nums.begin()+index);
vector<int> rightNums(nums.begin()+index+1,nums.end());
root->left=constructMaximumBinaryTree(leftNums);
root->right=constructMaximumBinaryTree(rightNums);
return root;
}
};原理思路:
Leetcode:106. 从中序与后序遍历序列构造二叉树、105. 从前序与中序遍历序列构造二叉树(C++)_Cosmoshhhyyy的博客-CSDN博客
与上一题思路完全相似,只是改变了切割标准而已,上一题会了,这题就明白了,具体可以看看上一个我文章,这里就不再写一遍解题思路了。同样这里也可以优化成利用索引直接在原数组上进行操作的代码,下面给出:
索引版本:
class Solution {
public:
TreeNode* traversal(vector<int>& nums, int left, int right)
{
if (left >= right) return NULL;
int index = left; // 分割点
for (int i = left + 1; i < right; ++i)
{
if (nums[i] > nums[index]) index = i;
}
TreeNode* root = new TreeNode(nums[index]);
root->left = traversal(nums, left, index);
root->right = traversal(nums, index + 1, right);
return root;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums)
{
return traversal(nums, 0, nums.size());
}
};