先给自己叠甲,记录自己的学习过程,如有内容错误欢迎指正!!!。
1. NSGA算法简介(Nondominated Sorting Genetic Algorithm)
根据标题,NSGA算法分为两个要点,Nondominated Sorting(非支配排序)和Genetic Algorithm(遗传算法)遗传算法讲解文章。
因此本文主要介绍非支配排序和算法本身的内容,对遗传算法仅作简要提及。
1.1 基本概念
要明白非支配的含义,自然要知道支配(dominated)的含义。

从字面意思上看来看,A “能力” 大于B,A就能够支配B。
在多目标优化问题中,涉及到多个目标。
如果一个解在所有目标上都不比另一个解差,并且在至少一个目标上更好,那么这个解被称为支配另一个解。
具体来说,假设有两个解
A
A
A和
B
B
B,如果对于所有的目标函数
F
(
X
)
F(X)
F(X)都有
F
(
A
)
≤
F
(
B
)
F(A)≤F(B)
F(A)≤F(B),并且至少存在一个目标函数
f
i
f_i
fi使得
f
i
(
A
)
<
f
i
(
B
)
f_i(A)<f_i(B)
fi(A)<fi(B),那么我们就说解A支配解B。
俗话来讲,就是“我哪哪都与你一样,但有一项能力比你强,我就能支配你。(当然,方方面面比你强,当然也能支配你)”
下面用一个草图简单表述这个意思。
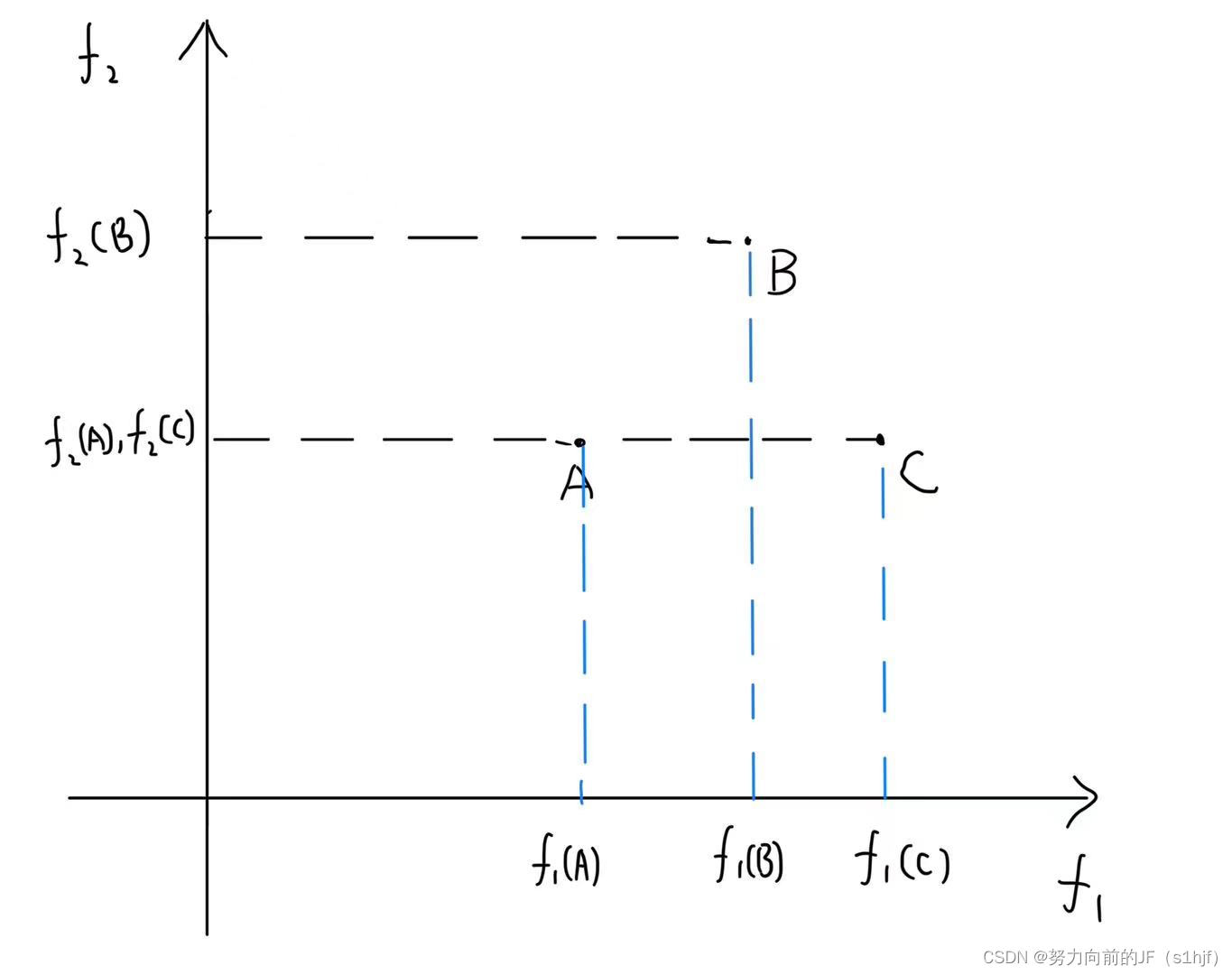
该问题是
m
i
n
F
(
X
)
,
即最小化优化问题。目标函数
F
内有两个子函数
f
1
和
f
2
。
该问题是min F(X),即最小化优化问题。目标函数F内有两个子函数f_1和f_2。
该问题是minF(X),即最小化优化问题。目标函数F内有两个子函数f1和f2。
对于A和B而言,
F
(
A
)
≤
F
(
B
)
,
且
f
1
(
A
)
<
f
1
(
B
)
;
f
2
(
A
)
<
f
2
(
B
)
F(A)≤F(B),且f_1(A)<f_1(B);f_2(A)<f_2(B)
F(A)≤F(B),且f1(A)<f1(B);f2(A)<f2(B)
满足
当解
A
在所有目标上都不比解
B
差,并且在至少一个目标上优于解
B
。
当解A在所有目标上都不比解B差,并且在至少一个目标上优于解B。
当解A在所有目标上都不比解B差,并且在至少一个目标上优于解B。
所以说,解A 支配 解B。
对于A和C而言,
F
(
A
)
≤
F
(
C
)
,
且
f
1
(
A
)
<
f
1
(
C
)
;
f
2
(
A
)
=
f
2
(
C
)
F(A)≤F(C),且f_1(A)<f_1(C);f_2(A)=f_2(C)
F(A)≤F(C),且f1(A)<f1(C);f2(A)=f2(C)
满足
当解
A
在所有目标上都不比解
C
差,并且在至少一个目标上优于解
C
。
当解A在所有目标上都不比解C差,并且在至少一个目标上优于解C。
当解A在所有目标上都不比解C差,并且在至少一个目标上优于解C。
所以说,解A 支配 解C。
注意!!!
解A 支配 解B时,解A称之为支配解(Dominating Solution),那解B呢? 非支配解?
千万注意!!!解B 不是 非支配解,解B称之为被支配解(Dominated Solution)。
那何为非支配解(Non-dominating Solution)???
非支配解是指在解集合中没有任何其他解可以支配它的解。
解集合中有A、B和C三个解。B和C都不能支配A。
此时解A成为非支配解。
当然,现实中的多目标优化问题不会只有三个解,往往有许多解。
我们还以两个优化目标举例,如下图。
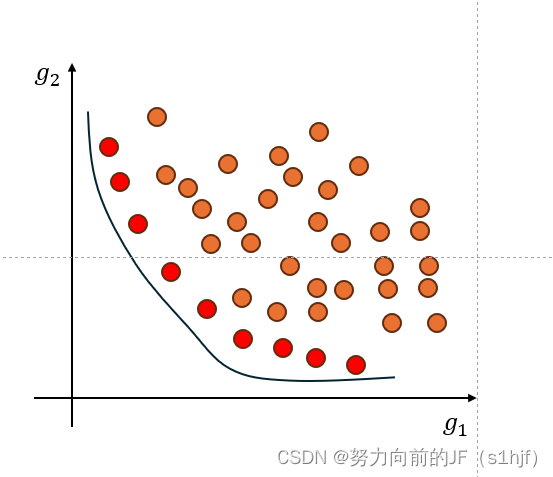
求解
m
i
n
G
(
X
)
,
在目标约束下,所有的解如上图所示。
求解 min G(X),在目标约束下,所有的解如上图所示。
求解minG(X),在目标约束下,所有的解如上图所示。
可以发现,红色的点无法被继续优化。当
g
1
g_1
g1减小时,
g
2
g_2
g2就会增大;当
g
2
g_2
g2减小时,
g
1
g_1
g1就会增大。
这些红色点所代表的解即为非支配解(它也称为帕累托解(Pareto Solution))
这些非支配解组成的集合称之为 帕累托最优集 ,这些解在目标空间中形成了 帕累托前沿(上图里面的黑色实线)。
帕累托前沿(Pareto Front) 是多目标优化问题中的一个关键概念,它是 帕累托最优解集(Pareto Optimal Set) 在目标空间中的表示。帕累托前沿是目标空间中所有帕累托解的集合,它展示了不同目标之间的最佳权衡。
注意!!!
帕累托解和非支配解的定义是基于解之间的比较,因此它们都是相对于问题中的解集合而言的。帕累托前沿是针对目标空间的。
总结来说,非支配解和帕累托解在多目标优化中是等价的概念,它们都描述了在多个目标之间达到最佳权衡的解。在实际应用中,寻找帕累托最优解通常意味着寻找非支配解,因为这些解代表了在多个相互冲突的目标之间无法进一步改进的解决方案。
1.2 非支配排序
NSGA与传统的遗传算法的主要区别在于:该算法在选择“基因”执行之前根据解之间的支配关系进行了分层。其选择“基因”、交叉“基因”和变异“基因”与传统的遗传算法没有区别。
假如每代保留10个解,但本代的帕累托最优集中有50个解。使用基于拥挤策略的虚拟适应度值进行调整,并确定每个种群的虚拟适应度值,然后根据虚拟适应度值的大小,确定优先选择进行处理的种群。
这里与传统遗传算法的适应度原理类似。遗传算法中以个体适应度的大小来判定各个个体的优劣程度,从而决定其遗传机会的大小。
考虑一个规模大小为N的种群,通过非支配排序算法可以对该种群进行分层,具体的步骤如下:

通过上述步骤得到的非支配个体集是种群的第一级非支配层;然后,忽略这些标记的非支配个体,再遵循步骤(1)一(4),就会得到第二级非支配;依此类推,直到整个种群被分级。
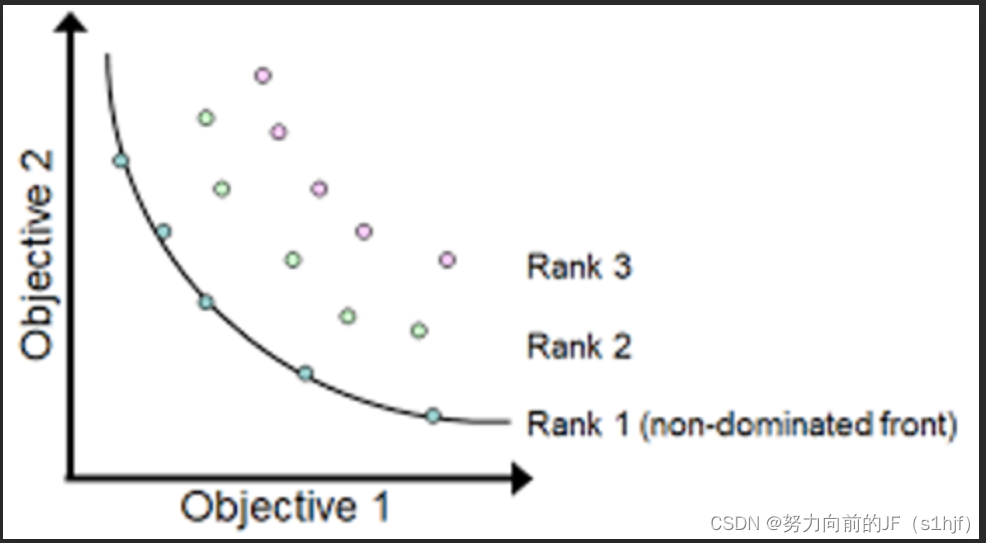
在对种群进行非支配排序的过程中,需要给每一个非支配层指定一个虚拟适应度值。级数越大,虚拟适应度值越小(Rank 2 的虚拟适应度小);反之,虚拟适应度值越大(Rank 1 的虚拟适应度大)。这样可以保证在选择操作中等级较低的非支配个体有更多的机会被选择进入下一代,使得算法以最快的速度收敛于最优区域(也就是说,让当前的帕累托最优集内的解参与遗传迭代)。另一方面,为了得到分布均匀的Pareto最优解集,就要保证当前非支配层上的个体具有多样性。(解所处的空间位置不能太拥挤,要保留一定的间距)
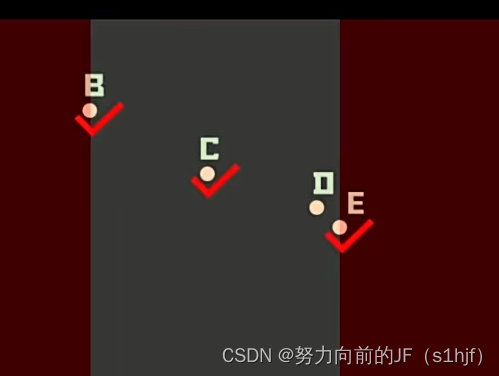
C点更能够代表B、E两点之间的信息,而不会去选择D点。
不断完成迭代,能够求出多目标优化问题的帕累托集。
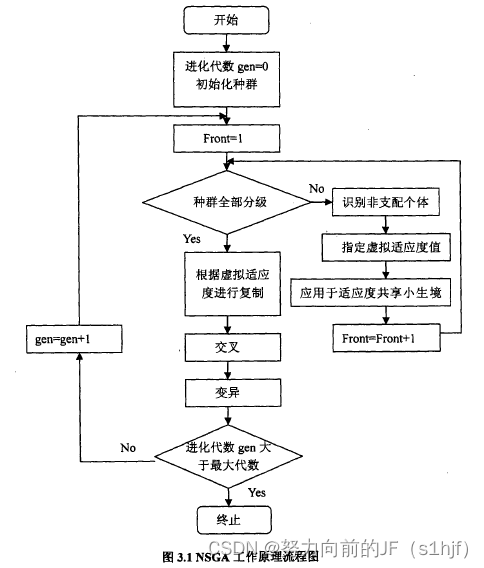
当然不一定能够求出全局最优解,但对于现实问题,以一个较快的运算速度求出非常接近全局最优解的解集,能够满足实际需要,即完成了优化的目标。
参考:
从NSGA到 NSGA II,
我翔哥的文章
数之道37】多目标优化求解策略与遗传算法NSGA-II<最优化系列第3集>