（ELA）Efficient Local Attention for Deep Convolutional Neural Networks

论文链接：ELA: Efficient Local Attention for Deep Convolutional Neural Networks (arxiv.org)

作者：Wei Xu, Yi Wan

单位：兰州大学信息科学与工程学院，青海省物联网重点实验室，青海师范大学

引用：Xu W, Wan Y. ELA: Efficient Local Attention for Deep Convolutional Neural Networks[J]. arXiv preprint arXiv:2403.01123, 2024.

摘要

众所周知，图像的空间维度包含关键的位置信息，而现有的注意力机制要么无法有效利用这种空间信息，要么以降低通道维数为代价。为了解决这些局限性，本文提出了一种高效局部注意力（Efficient Local Attention，ELA）方法，通过分析Coordinate Attention(CA) method的局限性，确定了Batch Normalization中泛化能力的缺乏、降维对通道注意力的不利影响以及注意力生成过程的复杂性。为了克服这些挑战，提出了结合一维卷积和Group Normalization特征增强技术。这种方法通过有效地编码两个一维位置特征图，无需降维即可精确定位感兴趣区域，同时允许轻量级实现。与2D卷积相比，1D卷积更适合处理序列信号，并且更轻量、更快。GN与BN相比，展现出可比较的性能和更好的泛化能力。

与 CA 类似，ELA 采用strip pooling在空间维度上获取水平和垂直方向的特征向量，保持窄核形状以捕获长程依赖关系，防止不相关区域影响标签预测，从而在各自方向上产生丰富的目标位置特征。ELA 针对每个方向独立处理上述特征向量以获得注意力预测，然后使用点乘操作将其组合在一起，从而确保感兴趣区域的准确位置信息。

Method

Coordinate Attention

CA包括两个主要步骤：坐标信息嵌入和坐标注意力生成。在第一步中，通过使用strip pooling而不是spatial global pooling来捕捉长距离的空间依赖性。

考虑一个卷积块的输出为 $R^{H\times W\times C}$ ，分别H，W，C代表高度、宽度和通道维度（即卷积核的数量）。第一步中，为了应用strip pooling，分别在两个空间范围内对每个通道执行平均池化：$(H,1)$ 在水平方向上和 $(1,W)$ 在垂直方向上，数学表示如下：

$$z_c^h(h)=\frac{1}{H}\sum _{0\le i<H}{x}_c(h,i)$$

$$z_c^w\left(w\right)=\frac{1}{W}\sum _{0\le j<W}{x}_c(j,w)$$

第二步中，由上述两个方程生成的特征图被聚合成为新的特征图，然后被送入共享转换函数 $F_1$（一个2D卷积）以及批量归一化（BN），可以表示如下。

$$f=\delta (BN(F_1(\left[z^h,z^w\right])))$$

其中，级联操作 $[.,.]$ 沿空间维，$\delta$ 表示非线性激活函数。中间特征图 $R^{C/r\times (H+W)}$，是水平和垂直编码后得到的。随后，$f^h\in R^{C/r\times H}$，$f^h\in R^{C/r\times H},f^w\in R^{C/r\times W}$，沿着空间维度。此外，另外两个$1\times 1$卷积变换 $F_h$ 和 $F_w$用于生成与输入通道数相同的张量。

$$g_c^h=\sigma (F_h(f^h))$$

$$g_c^w=\sigma (F_w(f^w))$$

其中，$\delta$ 表示sigmoid函数。为了降低计算开销，通常适当的减少$f$的通道数，比如32。最后得到输出 $g_c^h$ 和 $g_c^w$ ，被扩展并用作注意力权重，分别对应于水平和垂直方向。最终，CA 模块的输出可以表示为 $Y$：

$$y_c(i,j)=x_c(i,j)\times g_c^h(i)\times g_c^w(j)$$

通道维度的降低旨在减少模型的复杂性，但会影响通道与它们对应权重之间的关联，这可能会对整体的注意力预测产生不利影响。

Shortcomings of Coordinate Attention

BN极大地依赖于小批量的大小，当小批量过小时，BN计算出的均值和方差可能无法充分代表整个数据集，这可能会损害模型的总体性能。最开始CA中获得的坐标信息嵌入表示了每个通道维度内的序列信息，将BN放置在处理序列数据的网络中并不是最佳选择，特别是对于CA。

因此，CA可能会对较小的网络架构产生负面影响。相反，当GN被用作CA中BN的替代品，并融入到较小的网络架构中时，性能立即出现显著提升。此外，对CA结构的深入分析可以揭示额外的挑战。在第二步的开始，两个方向的特征图和被拼接成一个新的特征图，随后进行编码。然而，两个方向的特征图和具有独特的特性。因此，一旦合并并捕捉到它们的特点，它们各自连接处的相互影响可能会削弱每个方向上注意力预测的准确性。

Efficient Local Attention

CA方法通过利用strip pooling来捕获空间维度中的长距离依赖，显著提高了准确度，尤其是在更深层的网络中。基于之前的分析，可以看出BN阻碍了CA的泛化能力，而GN（组归一化）则解决了这些不足。

因为第一步中得出的位置信息嵌入是通道内的序列信号。因此，通常更合适的是使用1D卷积而不是2D卷积来处理这些序列信号。1D卷积不仅擅长处理序列信号，而且与2D卷积相比，它更加轻量化。在CA的情况下，尽管两次使用了2D卷积，但它使用的是 $1\times 1$ 的卷积核，这限制了特征提取能力。因此，ELA采用5或7大小的1D卷积核，这有效地增强了位置信息嵌入的交互能力，使得整个ELA能够准确找到感兴趣的区域。

$z_h$ 和 $z_w$ 不仅捕捉了全局感知场，还捕捉了精确的位置信息。为了有效地利用这些特征，作者设计了一些简单的处理方法。对两个方向（水平和垂直）上的位置信息应用一维卷积以增强其信息。随后，使用组归一化 $G_n$ 来处理增强的位置信息，可以得到在水平和垂直方向上的位置注意力的表示：

$$\begin{array}{c}{y}^h=\sigma (G_n(F_h(z_h)))\\ y^w=\sigma (G_n(F_w(z_w)))\end{array}$$

其中，$\sigma$ 为非线性激活函数， $F_h$ 和 $F_w$ 表示一维卷积，卷积核设置为5或7。尽管参数数量略有增加，但大小为 $7$ 的卷积核表现更好。

Multiple ELA version settings

为了在考虑参数数量的同时优化ELA的性能，引入了四种方案：ELA-Tiny(ELA-T)，ELA-Base(ELA-B)，ELA-Small(ELA-S)和ELA-Large(ELA-L)。

1. ELA-T的参数配置为 kernel size = 5, groups = in channels, num group = 32；
2. ELA-B的参数配置为 kernel size = 7, groups = in channels, num group = 16；
3. ELA-S的参数配置为 kernel size = 5, groups = in channels/8, num group = 16；
4. ELA-L的参数配置为 kernel size = 7, groups = in channels/8, num group = 16；

Visualization

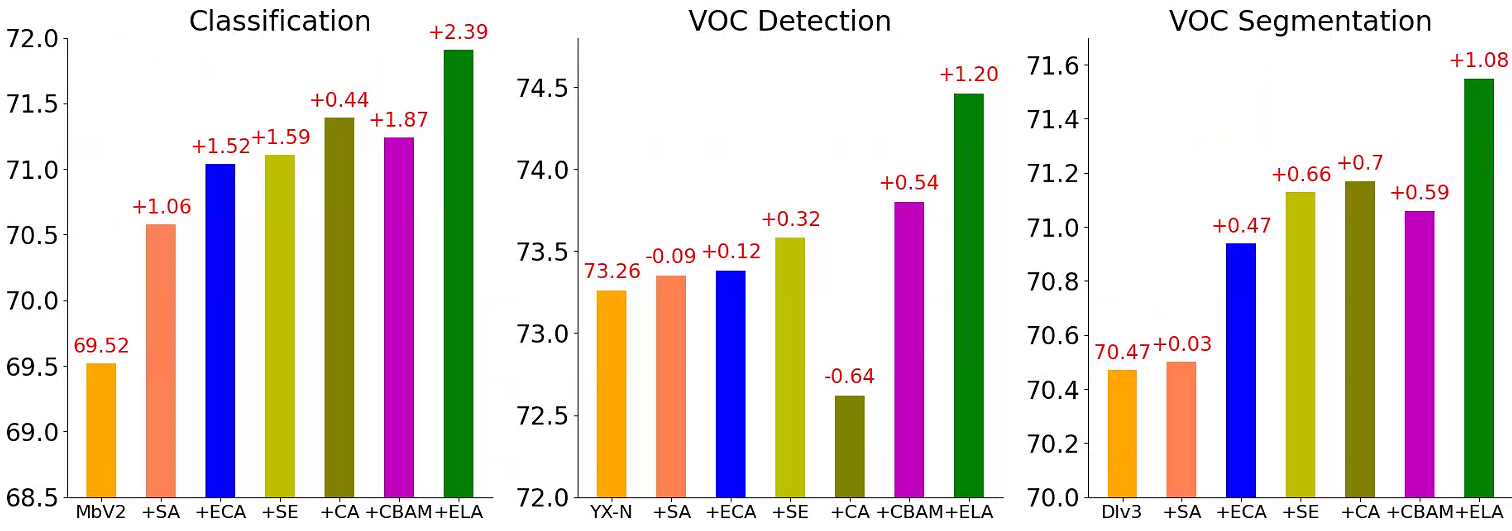
为了评估ELA方法的有效性，作者在ImageNet上进行了两组实验：ResNet（不包含注意力模块）和ELA-ResNet（包含ELA）。为了评估性能，作者使用了五张图像进行测试。通过使用GradCAM生成视觉 Heatmap ，作者在第四层（最后一个阶段的最后瓶颈）展示了两组模型的成果。下图说明了作者提出的ELA模块成功指导整个网络更精确地聚焦于目标细节的相关区域。这一演示突显了ELA模块在提高分类准确度方面的有效性。

Implementation

实验