Model-Free Q-Learning for the Tracking Problem of Linear Discrete-Time Systems,2024, Chun Li , Jinliang Ding , Senior Member, IEEE, Frank L. Lewis , Life Fellow, IEEE, and Tianyou Chai , Life Fellow, IEEE
对完全未知动力学的线性离散时间系统,提出model-free Qlearning 算法,解决最优跟踪问题。给出Qlearning性能指标函数,将跟踪问题转化为整定问题。对比ADP和Qlearning,性能指标函数在控制输入的二次型增加一个由增益矩阵和参考跟踪轨迹组成的乘积项。该Qlearning不需要原控制系统和指令生成器的任何动力学知识,在线获取系统状态、控制输入和参考跟踪轨迹等信息,迭代推导控制策略。通过被控系统和参考跟踪轨迹前提下得到的迭代标准,可更新期望的控制输入,保证所得到的控制策略可消除跟踪误差。为数据的高效利用,该算法采用off-policy。
以往文章对CT和DT系统的输出跟踪问题,提出基于内部模型原理的ADP和Qlearning。与其不同,状态跟踪问题则采用设计增广系统。根据B. Kiumarsi and F. L. Lewis, “Actor-critic-based optimal tracking for partially unknown nonlinear discrete-time systems,” IEEE Trans. Neural Netw. Learn. Syst., vol. 26, no. 1, pp. 140–151, Jan. 2015.中其ADP和Qlearning会导致有界跟踪误差,无法消除。
控制输入变量维数小于系统状态维数,期望控制输入不总是由输入矩阵的逆求得。为避免获得期望控制输入,由原控制系统和指令生成器组成的增广系统,以形成HJB方程和ARE。选择较小折扣因子或增加跟踪误差二次型在性能指标函数中的比例有利于减小跟踪误差。
当系统动力学未知时,数据驱动方法非常适合。Y. Jiang, J. Fan, W. Gao, T. Chai, and F. L. Lewis, “Cooperative adaptive optimal output regulation of nonlinear discretetime multi-agent systems,” Automatica, vol. 121, Nov. 2020, Art. no. 109149.,每个智能体基于实时数据建模,其为基于数据驱动的模型。而Qlearning利用在线数据迭代更新Qfunction和policy function。B. Kiumarsi, F. L. Lewis, H. Modaresa, A. Karimpoura, and M.-B. Naghibi-Sistani, “Reinforcement Q-learning for optimal tracking control of linear discrete-time systems with unknown dynamics,” Automatica, vol. 50, no. 4, pp. 1167–1175, 2014.对线性离散时间系统的OTC问题提出基于增广系统的数据驱动的Qlearning方法。
线性离散时间系统

指令生成器的动力学
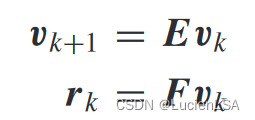
跟踪控制问题转化为整定问题
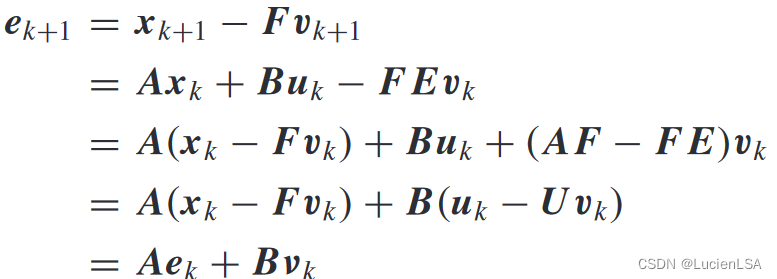
值函数定义为
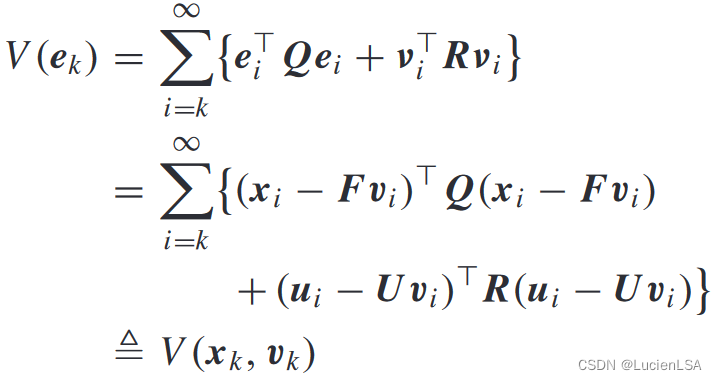
给出最优值函数和贝尔曼方程,构造哈密顿函数
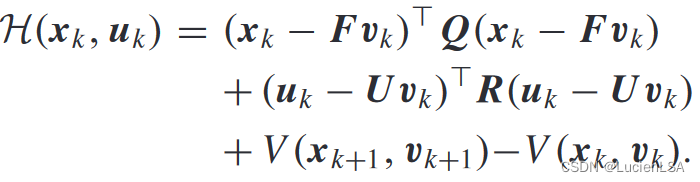
最优控制的平稳性条件,得到最优控制输入
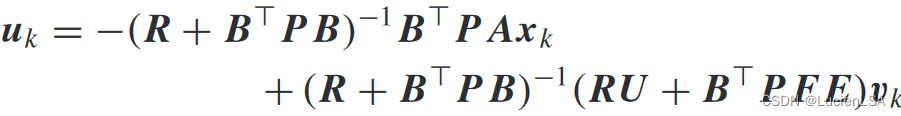
其形式为
u
k
=
−
K
x
k
+
L
v
k
u_k=-Kx_k+Lv_k
uk=−Kxk+Lvk
K
=
(
R
+
B
⊤
P
B
)
−
1
B
⊤
P
A
K=(R+B^\top PB)^{-1}B^\top PA
K=(R+B⊤PB)−1B⊤PA,
L
=
U
+
K
F
\boldsymbol{L}=\boldsymbol{U}+\boldsymbol{K}\boldsymbol{F}
L=U+KF
定义Qfunction(Qlearning的性能指标函数),值函数改写为
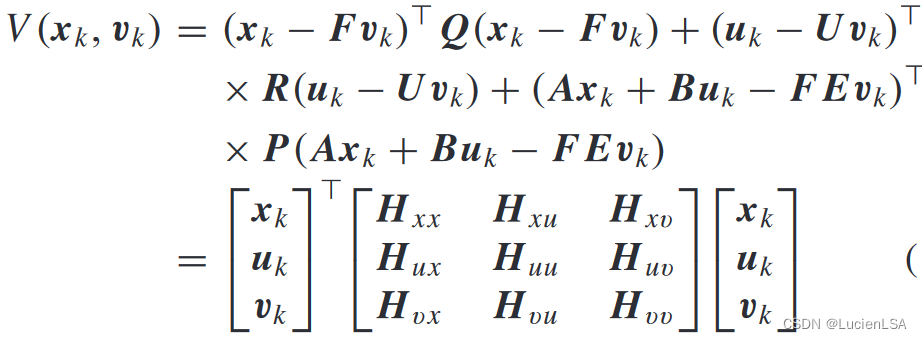
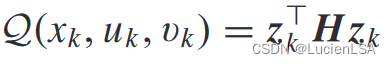
Qlearning方法贝尔曼方程
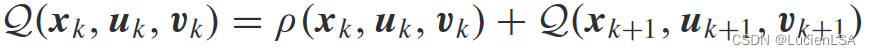
ρ
(
x
k
,
u
k
,
v
k
)
\rho\left(x_k,u_k,v_k\right)
ρ(xk,uk,vk)为效用函数
最优控制输入表示为
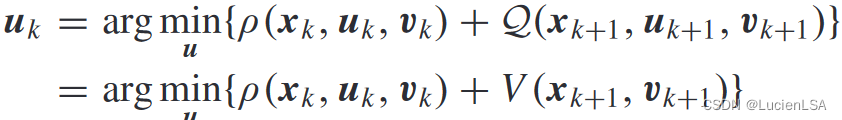
根据Qfunction核矩阵
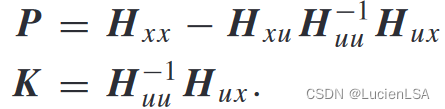
P和K求解通过原系统的整定问题,而不必考虑跟踪问题。
Lemma1给出增广矩阵[F;U]满足
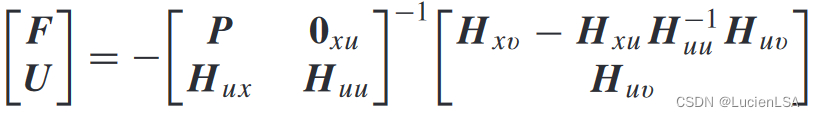
由于F未知,将以下作为增广矩阵[F;U]和H核矩阵的必要条件
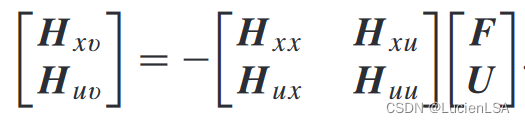
为使用数据驱动方法求解控制矩阵,定义激活函数
值迭代Qlearning方法,迭代Qfunction标准,
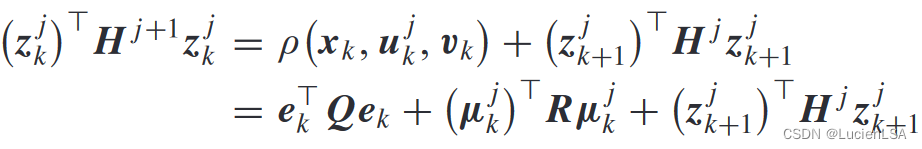
使用激活函数可将迭代Qfunction改写为
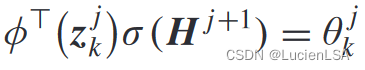
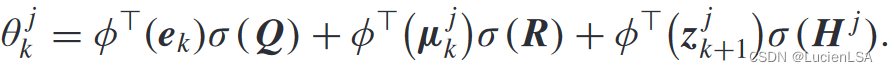
根据激活函数矩阵,满秩
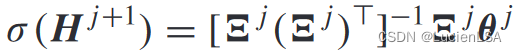
计算迭代核矩阵更新
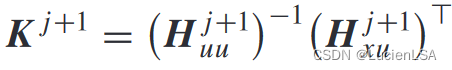
增广矩阵更新
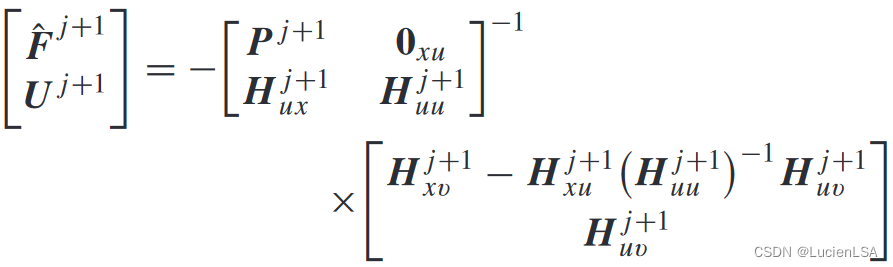
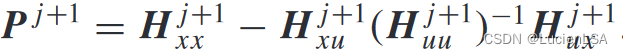
迭代核矩阵更新
Algorithm1 基于Vi的model-free Qlearning算法求解跟踪控制问题
初始化增广矩阵增益和Qfunction核矩阵,H、K、L、F、U。在线数据,计算权重向量,更新核矩阵和增益矩阵。
为确保矩阵可逆,传统方法需加入PE条件,即探测噪音。PE条件由随机噪声和正弦信号。需要更多样本数据有利于研究被控系统和指令生成器的动力学。
Lemma2给出在Assumptions1和2下跟踪问题由被控系统和指令生成器描述。矩阵U满足Assumption2的要求
Theorem1给出在Assumptions1和2,Qfunction定义下,在迭代Algorithm1,迭代矩阵[F,U]满足假设2,由Algorithm1得到的矩阵K和L以消除跟踪误差。
基于off-policy方法的Model-free Qlearning Algorithm
控制策略
u
k
=
−
K
x
k
u_k=-Kx_k
uk=−Kxk最优整定问题,求解整定问题的核矩阵为
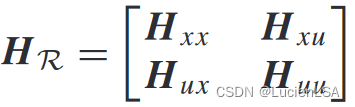
迭代控制输入和在线控制输入

迭代系统状态表示为
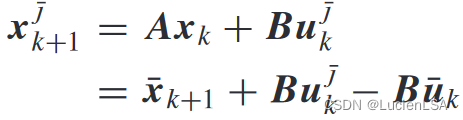
因此迭代值函数更新为
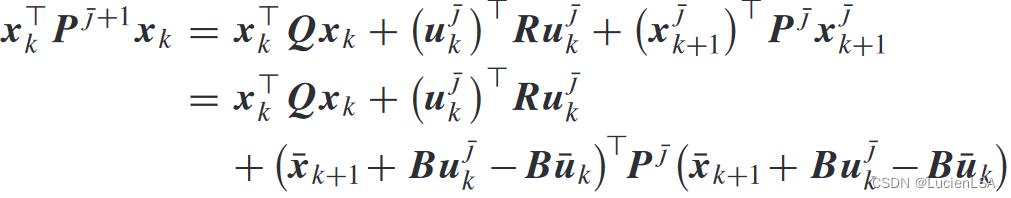
由于迭代值函数等价于Qfunction
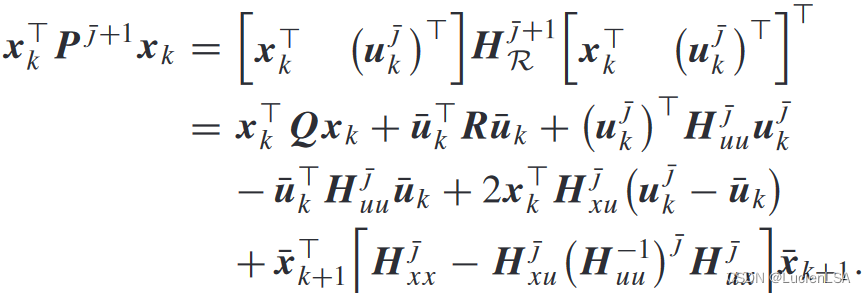
在激活函数下
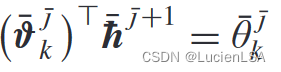
可更新迭代核矩阵
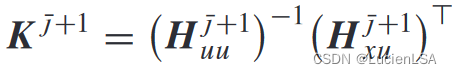
Algorithm2给出使用off-policy方法的基于VI的model-free Qlearning算法