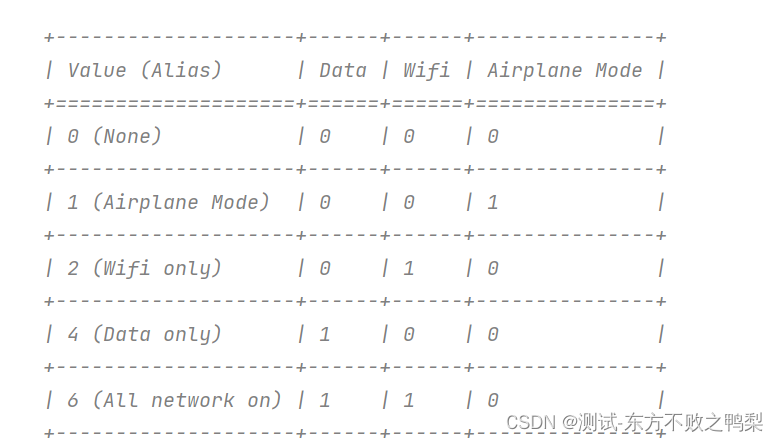
文章目录
- 简单题目
- MLE 在不同的分布的运用
- 正态分布
- 指数分布
- 均匀分布
- 泊松分布
简单题目
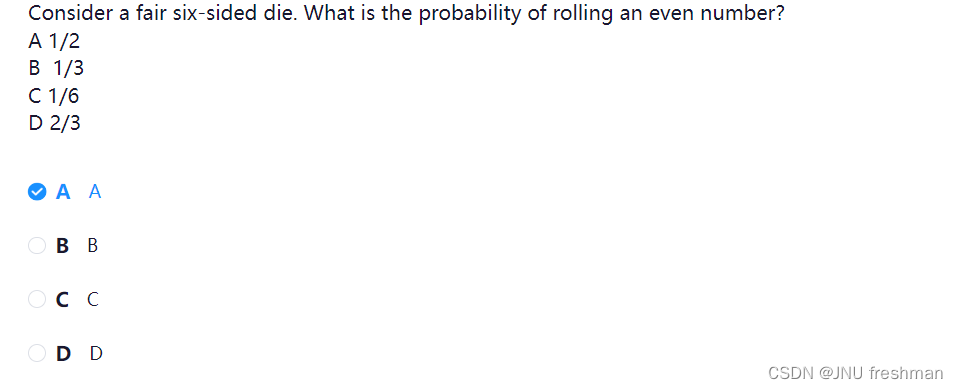
- 此题问的是求丢色子,求得到偶数点的概率
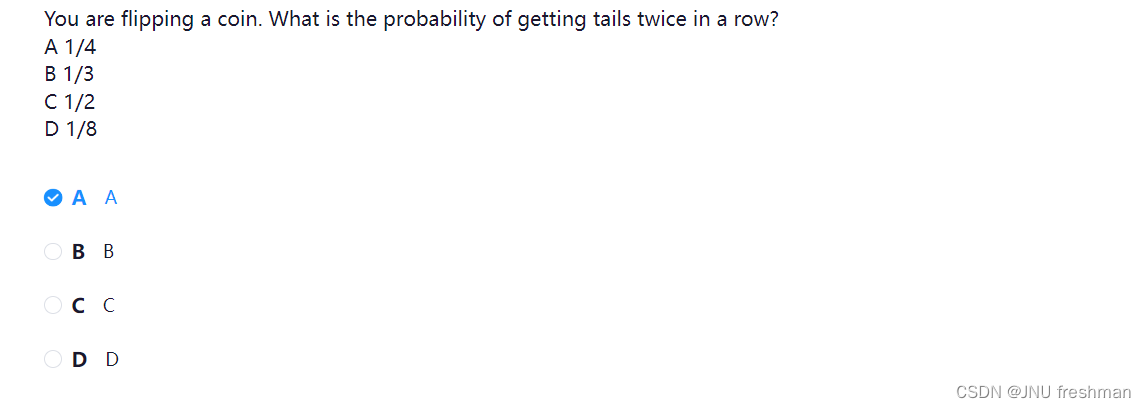
- 求两次都得到硬币的背面的概率

- 拿球问题
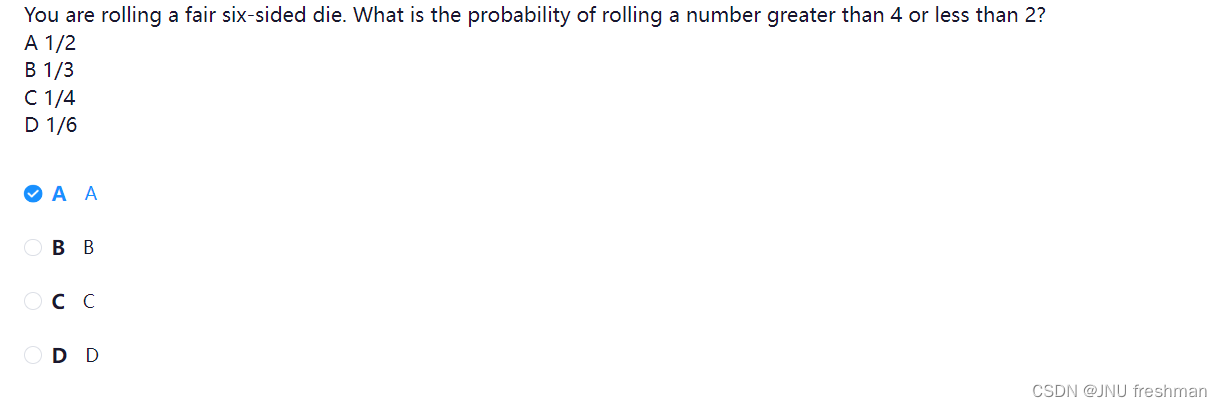
- 符合的点数是 1,5,6
MLE 在不同的分布的运用
正态分布
对于给定的数据集 {1, 3, 4, 6, 7},我们想要估计生成这些数据的正态分布的参数 μ 的最大似然估计(MLE)。
正态分布的概率密度函数(PDF)为:
f ( x ; μ , σ 2 ) = 1 2 π σ 2 exp ( − ( x − μ ) 2 2 σ 2 ) f(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) f(x;μ,σ2)=2πσ21exp(−2σ2(x−μ)2)
其中,( μ \mu μ) 表示平均值,( σ 2 \sigma^2 σ2 ) 表示方差。
对于给定的数据集,我们可以使用最大似然估计来找到最适合这些数据的参数( μ \mu μ) 。对于正态分布,( μ \mu μ) 的最大似然估计是数据的平均值。
因此,对于数据集 {1, 3, 4, 6, 7},( μ \mu μ) 的最大似然估计是这些数据的平均值:
μ ^ = 1 + 3 + 4 + 6 + 7 5 = 21 5 = 4.2 \hat{\mu} = \frac{1 + 3 + 4 + 6 + 7}{5} = \frac{21}{5} = 4.2 μ^=51+3+4+6+7=521=4.2
但由于选项中只有整数,我们应选择最接近 4.2 的整数。
最接近 4.2 的整数是 4。
所以,( μ \mu μ) 的最大似然估计是 4。
指数分布
对于给定的数据集 {2, 4, 6, 8, 10},我们想要估计一个指数分布的参数 l a m b d a lambda lambda的最大似然估计(MLE)。
指数分布的概率密度函数(PDF)为:
f ( x ; λ ) = λ e − λ x f(x; \lambda) = \lambda e^{-\lambda x} f(x;λ)=λe−λx
对于给定的数据集,我们可以使用最大似然估计来找到最适合这些数据的参数 l a m b d a lambda lambda.对于指数分布, l a m b d a lambda lambda的最大似然估计是数据的倒数的平均值。
因此,对于数据集 {2, 4, 6, 8, 10}, l a m b d a lambda lambda 的最大似然估计为:
h a t λ = n ∑ i = 1 n x i hat{\lambda} = \frac{n}{\sum_{i=1}^{n} x_i} hatλ=∑i=1nxin
其中,( n ) 是数据集的大小,( x i x_i xi ) 是数据集中的第 ( i ) 个数据点。
对于给定的数据集,( n = 5 ),( s u m i = 1 n x i = 2 + 4 + 6 + 8 + 10 = 30 sum_{i=1}^{n} x_i = 2 + 4 + 6 + 8 + 10 = 30 sumi=1nxi=2+4+6+8+10=30)。
因此:
[ h a t λ = 5 30 = 1 6 hat{\lambda} = \frac{5}{30} = \frac{1}{6} hatλ=305=61]
所以, l a m b d a lambda lambda 的最大似然估计为 ( 1 6 \frac{1}{6} 61 )。
所以答案是:
B) 1/6
均匀分布
对于给定的数据集 {10, 15, 20, 25, 30},我们想要估计一个在区间 (0, θ) 上的均匀分布的参数 ( \theta ) 的最大似然估计(MLE)。
在均匀分布中,所有在指定区间内的值都是等可能的。因此,我们可以选择数据集中的最大值作为参数 ( \theta ) 的估计值。
因此,对于数据集 {10, 15, 20, 25, 30},最大值是 30,因此 ( \theta ) 的最大似然估计是 30。
所以答案是:
D) 30
泊松分布
对于给定的数据集 {3, 5, 7, 9, 11},我们希望估计生成这些数据的泊松分布的参数 μ 的最大似然估计(MLE)。
泊松分布用于描述在固定时间或空间范围内随机事件发生的次数,其概率质量函数为:
P ( X = k ) = e − μ μ k k ! P(X = k) = \frac{e^{-\mu} \mu^k}{k!} P(X=k)=k!e−μμk
其中,( k ) 表示事件发生的次数,( μ \mu μ ) 表示平均发生次数。
对于给定的数据集,泊松分布参数( μ \mu μ ) 的最大似然估计是数据的平均值。
因此,对于数据集 {3, 5, 7, 9, 11},( μ \mu μ ) 的最大似然估计是这些数据的平均值:
[ μ ^ = 3 + 5 + 7 + 9 + 11 5 = 35 5 = 7 \hat{\mu} = \frac{3 + 5 + 7 + 9 + 11}{5} = \frac{35}{5} = 7 μ^=53+5+7+9+11=535=7 ]
所以答案是:
D) 7