题目描述:
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m)处,至少需要移动多少次。
数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n和 m。
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例:
8思路:
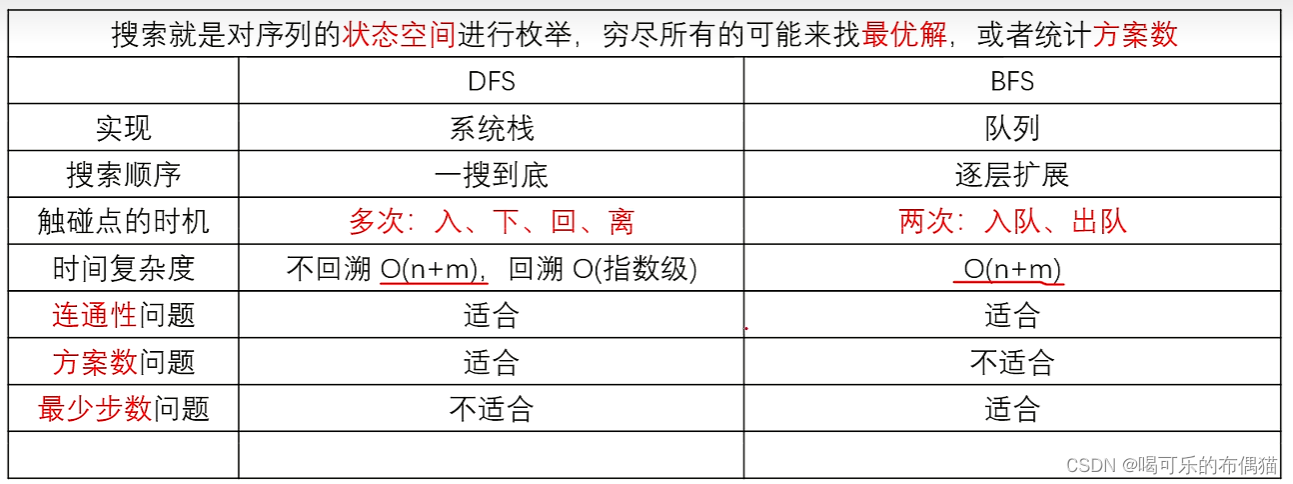
根据算法的特性此题我们选择使用宽搜算法,逐层枚举,求出最短路径 。

根据上面的宽搜树,逐层开始搜索即可。 树根是(0,0)从此起点开始逐层开搜
第一层是(1,0),接着第二层是(2,0),第三层是(2,1)和(3,0)
第四层是(2,2),(4,0),第五层是(1,2)和 (4,1) 和(2,3)
第六层是(0,2).。。。。。。。。后面按照题目规则上下左右找就像,
这里有一个知识点就是如何能方便上下左右去走,这个时候就要设置一个上下左右的偏移量,设中间数是(x,y)往上走一个单位就是(x-1,y),往右走一个单位就是(x,y+1),往下走一个单位就是(x+1,y),往左走一个单位是(x,y-1);
大家可以结合此文上下两张图自己走一遍。树形式是方便我们更好的理解,实际实现是用一个队列实现。(个人理解)

AC代码:
第一种手写队列:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<utility>
using namespace std;
typedef pair<int,int> PII;//定义一个二元组
const int N = 110;
int g[N][N];//存的地图
int d[N][N];//每个点到终点的距离
int n,m;
PII q[N*N],pre[N][N];//存坐标手写队列
//输出路径
void print(int x,int y)
{
if(x==1 && y==1) return;
auto t = pre[x][y];
print(t.first,t.second);
printf("%d %d\n",t.first,t.second);
}
int bfs(int a,int b)
{
//队列的头,和尾(从1开始)
int hh = 1,tt = 1;
q[1] = {a,b};//存入第一个点,也是起点
//把没走的点都标记成-1
memset(d,-1,sizeof d);
d[1][1] = 0;//起点开始走; 也就是所谓的第0步
//设置上下左右偏移量
int dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1};
while(hh <= tt)
{
//取出队首元素
auto t = q[hh++];
for(int i=0;i<4;i++)
{
//算出上下左右能走的点的坐标
int x = t.first + dx[i],y = t.second+dy[i];
if(x >= 1 && y >= 1 && x<=n && y<=m && g[x][y] == 0 && d[x][y] == -1)
{
d[x][y] = d[t.first][t.second] + 1;
pre[x][y] = t;//存储当前点的前驱节点
q[++tt] = {x,y};//存当前下标.入队
}
}
}
return d[n][m];
}
int main()
{
cin >> n >> m;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
cin >> g[i][j];
cout << bfs(0,0) << endl;
return 0;
}第二种直接使用stl中的queue
#include<iostream>
#include<algorithm>
#include<cstring>
#include <queue>
#include<utility>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int g[N][N],d[N][N];
int n,m;
int bfs(int a,int b)
{
queue<PII> q;
q.push({a,b});
memset(d,-1,sizeof d);
d[0][0] = 0;
int dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1};
while(q.size())
{
auto t = q.front();
q.pop();
for(int i=0;i<4;i++)
{
int x = t.first + dx[i],y = t.second + dy[i];
if(x >= 0 && x < n && y >=0 && y < m && g[x][y] == 0 && d[x][y] == -1)
{
d[x][y] = d[t.first][t.second] + 1;
q.push({x,y});
}
}
}
return d[n-1][m-1];
}
int main()
{
cin >> n >> m;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
cin >> g[i][j];
cout << bfs(0,0) << endl;
return 0;
}以上图片来源于B站董晓算法和acwing视频