问题 1 根据附件 1 中的数据，分析生产线中各装置故障的数据特征，构建故障报警模型，实现故障的自动即时报警。

问题分析

针对问题一，我们的目标是利用附件1中提供的数据，分析生产线各装置发生故障的数据特征，并构建一个故障报警模型以实现故障的自动即时报警。下面解释对问题一是如何进行分析的：
基本思路如下：
数据预处理：首先，需要对附件1中的数据进行深入理解，包括但不限于生产线运行记录的字段含义、故障类型及其代码表示等。这涉及到数据清洗和预处理步骤，如处理缺失值、异常值和数据类型转换。

故障数据特征分析：分析各类故障发生的特征和模式。对时间序列数据的分析，如故障发生的时间点、频率，以及与故障相关联的其他变量（例如特定操作或装置状态）的关系。

模型构建：基于故障数据特征的分析结果，选择算法构建故障报警模型。采用机器学习模型（如决策树、随机森林、支持向量机等）或深度学习模型（如卷积神经网络、循环神经网络等）。模型的选择依赖于故障数据的特征和模式，以及模型的预测性能。

模型评估优化：通过交叉验证等方法对模型进行评估，并根据评估结果对模型进行调优。关注模型的准确性、召回率和其他相关性能指标，确保模型能够有效地预测故障发生。

具体求解过程
数据读入与预处理：首先，读入附件1中的数据，并进行预处理。这包括将文本数据（如生产线编号）转换为数值型数据，以便于后续处理。

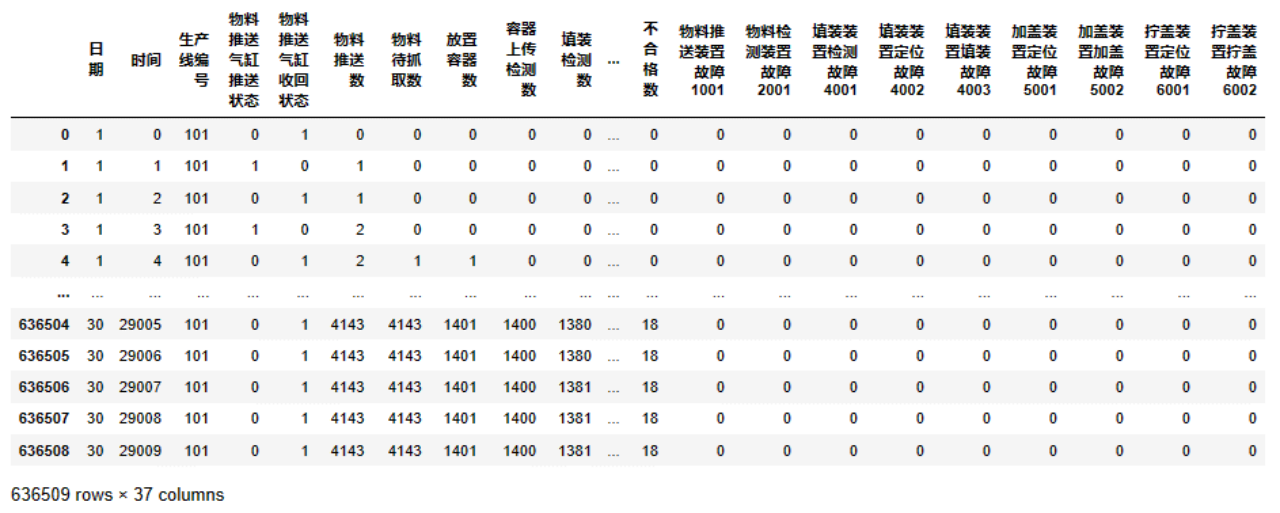
相关性分析：通过对数据集中的不同列（特征）进行分析，选出与故障发生相关性较大的特征。这一步是为了确定哪些特征对于故障预测更为关键。

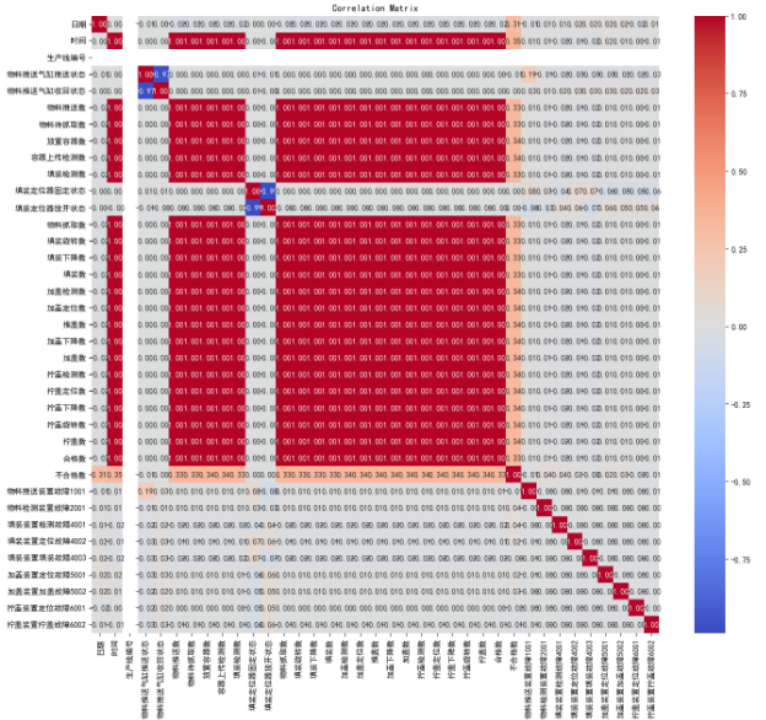
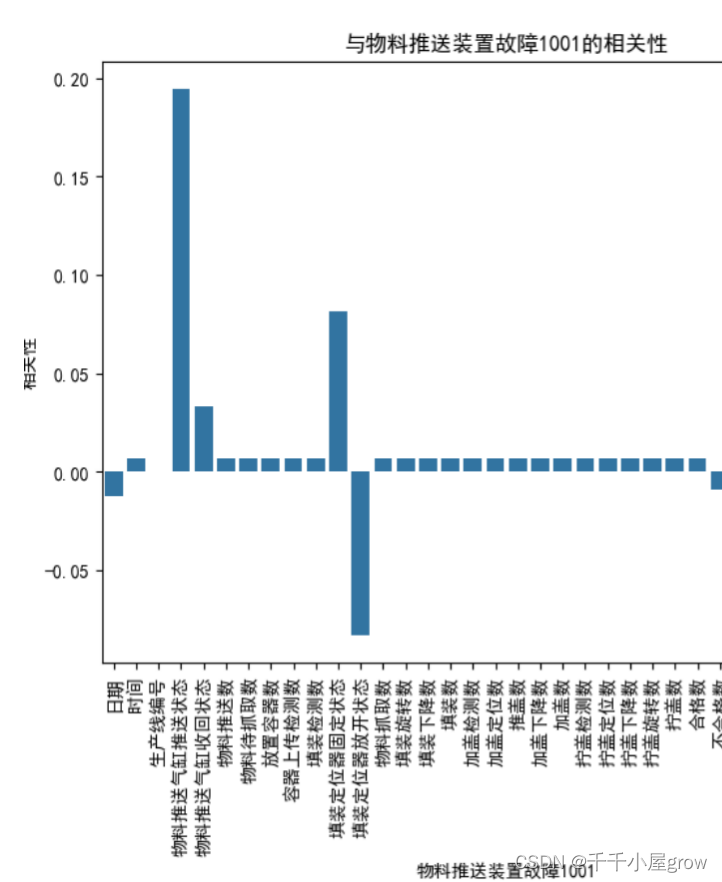
模型构建：采用了三种模型进行故障预测，包括xgboost模型、线性模型神经网络和LSTM（长短期记忆）模型。这些模型被用来预测生产线的故障发生，基于特定故障的相关性分析结果。

多标签分类：将问题视为一个多标签的线性回归问题，即每种故障状态都被视作一个标签，故障发生与否则对应于二值（0或1）输出。这意味着模型需要能够预测多种可能的故障状态。

数据上采样：为了解决数据集中故障样本量较少的问题，进行了数据上采样，将无故障与故障样本的比例调整为1:3，以增加模型训练时故障样本的权重。

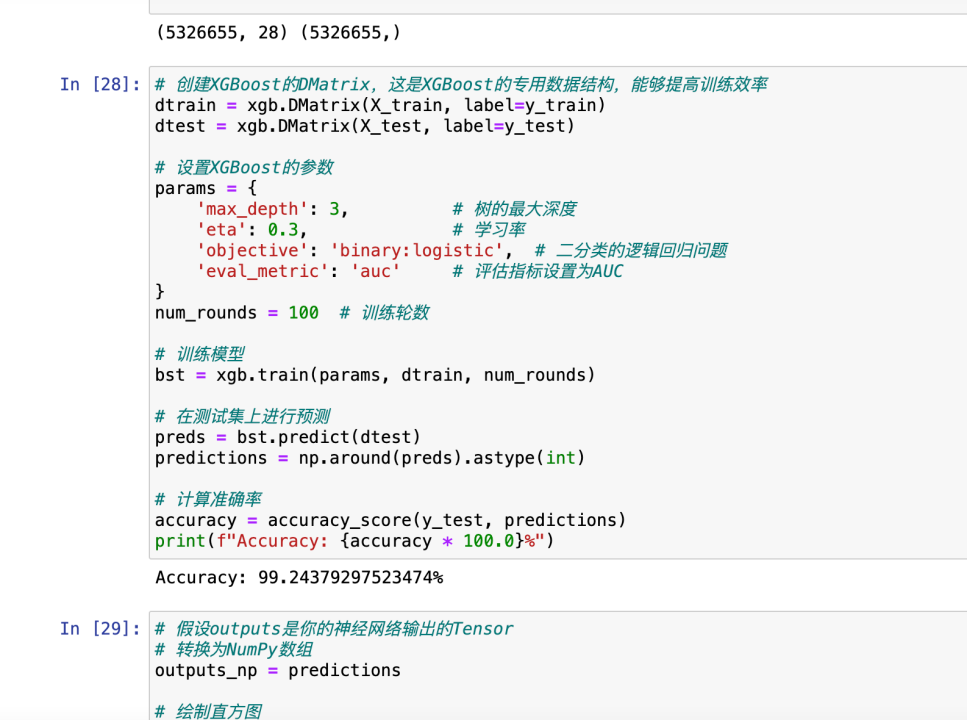
模型比较与选择：在三种模型中，推荐使用了xgboost模型，因为它在预测准确率方面表现最佳。准确率达到了99.2%，这是通过将数据集划分为训练集（70%）和测试集（30%）后，在测试集上获得的结果。

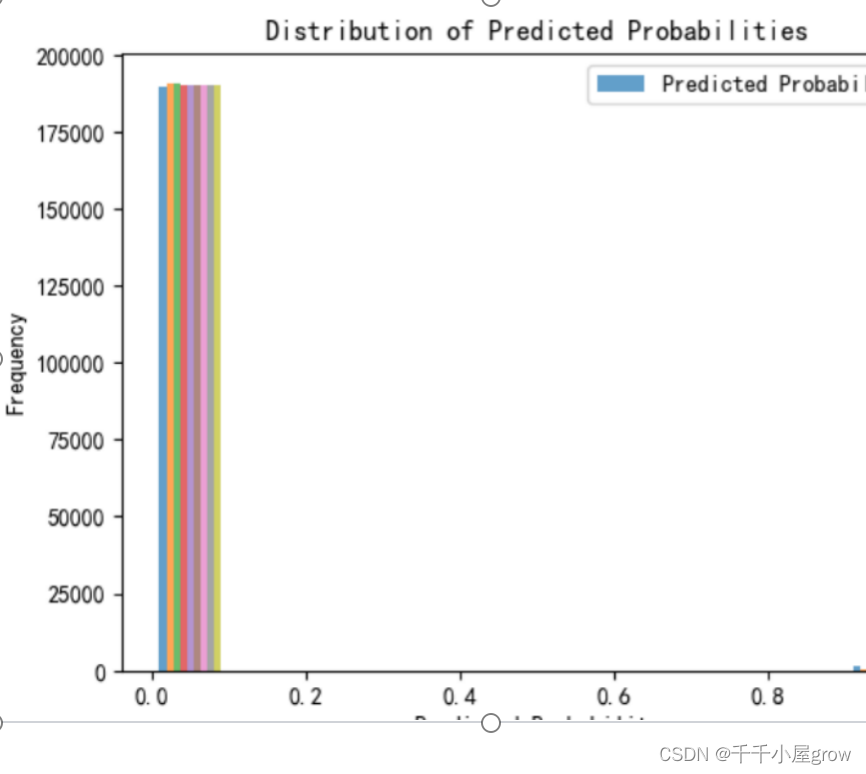
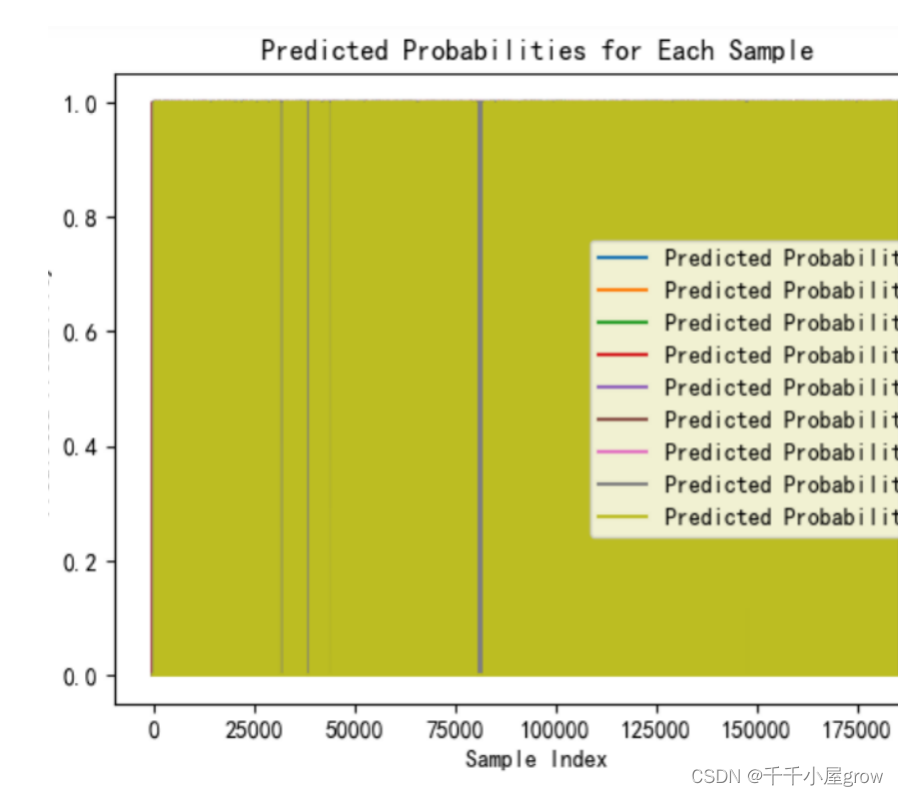
问题 2 应用问题 1 所建立的模型，对附件 2 中的数据进行分析判断，实现生产线中各 装置故障的自动即时报警，给出故障报警的日期、开始时间与持续时长，将结果存放到 result2.xlsx 中（格式见表 1，模板文件在附件 2 中），并在论文中给出每条生产线中各装置 每月的故障总次数及最长与最短的持续时长。

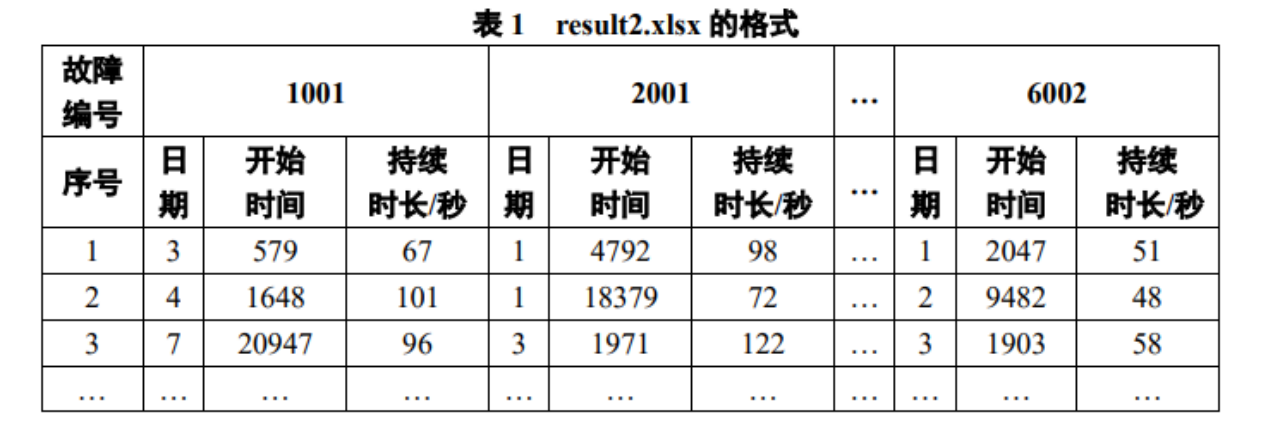
问题二主要是根据问题一构建的模型，预测并汇总附件二中的可能出现的故障情况。在获取附件2的数据后会进一步补充。

问题 3 根据附件 3 中的数据，分析产品的产量、合格率与生产线、操作人员等因素的
关系。
本题难度不大，但所提供示例数据仅包含一条生产线的，待完整数据给出会立刻更新。
首先，我们可以关注以下几个因素：
生产线编号：确定每条生产线的产量和质量表现。
操作人员：检查不同操作人员对产量和质量的影响。
物料推送数、填装数、加盖数、拧盖数：这些指标代表了生产过程中的关键步骤，与产量和质量密切相关。
合格数、不合格数：反映了产品的质量状况。
故障情况：各种装置的故障可能影响产量和质量。
从数学建模的角度，你可以采用多种方法来建立模型，以分析产品的产量、合格率与生产线、操作人员等因素之间的关系。以下是一种可能的建模方法：

3.1相关性分析：
选择变量：确定你想要分析的变量，包括产量、合格率以及可能影响这些指标的因素，如生产线编号、操作人员等。
计算相关系数：对于每对变量，计算其相关系数。如果是连续变量，可以使用皮尔逊相关系数；如果是顺序变量或者数据不满足正态分布，可以使用斯皮尔曼等级相关系数。
解释结果：根据相关系数的大小和方向来解释变量之间的关系。相关系数接近于1表示正相关关系，接近于-1表示负相关关系，接近于0表示无相关关系。
绘制相关性矩阵：可以绘制一个相关性矩阵，将各个变量之间的相关系数以矩阵的形式呈现，以便更直观地理解变量之间的关系。

3.2多元线性回归模型：
可以使用多元线性回归模型来探究生产线、操作人员以及其他因素对产量和质量的影响。首先，你需要将数据整理成适合回归分析的格式，其中每个样本代表一次生产过程，每个特征代表一个影响因素，例如生产线编号、操作人员编号、物料推送数、填装数等。然后，你可以使用回归分析来拟合一个模型，以预测产量和质量，并确定各个因素对产量和质量的影响程度。

问题 4 根据实际情况，现需要扩大生产规模，将生产线每天的运行时间从 8 小时增加
到 24 小时不间断生产。针对问题 3 的 10 条生产线，结合问题 3 的分析结果，考虑生产线与操作人员的搭配，制定最佳的操作人员排班方案，将结果存放到 result4-1.xlsx 和 result4-2.xlsx中（格式见表 2 和表 3，模板文件在附件 4 中），并在论文中给出最佳的排班方案及相关结果。
要求排班满足如下条件：
(1) 各操作人员做五休二，尽量连休 2 天；
(2) 各操作人员每班连续工作 8 小时；
(3) 班次时间：早班（8:00-16:00）、中班（16:00-24:00）、晚班（0:00-8:00）；
(4) 各工龄操作人员的人数比例与问题 3 中的比例相同；
(5) 各操作人员的班次安排尽量均衡。

本题是一个常见的规划类问题，需要根据所给数据确定目标函数（排班效率最高），和约束条件：人员非负，人员为整数，人员调动规则，题目所给出的5个条件等
最后需要考虑求解算法，具体可以采用遗传算法（调用ga包进行实现），模拟退化，蚁群算法等。

参考内容：
2024泰迪杯数据挖掘助攻合集
#复制打开
#docs.qq.com/doc/DVVlhb2xmbUFEQUJL