【深度学习】深度学习md笔记总结第2篇：TensorFlow介绍,学习目标【附代码文档】

深度学习笔记完整教程（附代码资料）主要内容讲述：深度学习课程，深度学习介绍要求,目标,学习目标,1.1.1 区别,学习目标,学习目标。TensorFlow介绍，2.4 张量学习目标,2.4.1 张量(Tensor),2.4.2 创建张量的指令,2.4.3 张量的变换,2.4.4 张量的数学运算,学习目标。TensorFlow介绍，1.2 神经网络基础学习目标。TensorFlow介绍，总结学习目标,1.3.1 神经网络,1.3.2 playground使用,学习目标,1.4.1 softmax回归,1.4.2 交叉熵损失。神经网络与tf.keras，1.3 Tensorflow实现神经网络学习目标,1.3.1 TensorFlow keras介绍,1.3.2 案例：实现多层神经网络进行时装分类。神经网络与tf.keras，1.4 深层神经网络学习目标。卷积神经网络，3.1 卷积神经网络(CNN)原理学习目标。卷积神经网络，3.1 卷积神经网络(CNN)原理学习目标。卷积神经网络，2.2案例：CIFAR100类别分类学习目标,2.2.1 CIFAR100数据集介绍,2.2.2 API 使用,2.2.3 步骤分析以及代码实现(缩减版LeNet5),学习目标。卷积神经网络，2.4 BN与神经网络调优学习目标。卷积神经网络，2.4 经典分类网络结构学习目标,2.4.6 案例：使用pre_trained模型进行VGG预测,2.4.7 总结。卷积神经网络，2.5 CNN网络实战技巧学习目标,3.1.1 案例：基于VGG对五种图片类别识别的迁移学习,3.1.2 数据增强的作用。卷积神经网络，总结学习目标,1.1.1 项目演示,1.1.2 项目结构,1.1.3 项目知识点,学习目标,1.2.1 安装。商品物体检测项目介绍，3.4 Fast R-CNN。YOLO与SSD，4.3 案例：SSD进行物体检测4.3.1 案例效果,4.3.2 案例需求,4.3.3 步骤分析以及代码,2.1.1 常用目标检测数据集,2.1.2 pascal voc数据集介绍,2.1.3 XML。商品检测数据集训练，5.2 标注数据读取与存储5.2.1 案例：xml读取本地文件存储到pkl,5.3.1 案例训练结果,5.3.2 案例思路,5.3.3 多GPU训练代码修改,5.4.1 预测代码,5.4.1 keras 模型进行TensorFlow导出。

全套笔记资料代码移步：前往gitee仓库查看

感兴趣的小伙伴可以自取哦，欢迎大家点赞转发~

全套教程部分目录：

部分文件图片：

TensorFlow介绍

说明TensorFlow的数据流图结构
应用TensorFlow操作图
说明会话在TensorFlow程序中的作用
应用TensorFlow实现张量的创建、形状类型修改操作
应用Variable实现变量op的创建
应用Tensorboard实现图结构以及张量值的显示
应用tf.train.saver实现TensorFlow的模型保存以及加载
应用tf.app.flags实现命令行参数添加和使用
应用TensorFlow实现线性回归

2.4 张量

学习目标

目标
知道常见的TensorFlow创建张量
知道常见的张量数学运算操作
说明numpy的数组和张量相同性
说明张量的两种形状改变特点
应用set_shape和tf.reshape实现张量形状的修改
应用tf.matmul实现张量的矩阵运算修改
应用tf.cast实现张量的类型
应用
无
内容预览
2.4.1 张量(Tensor)
- 1 张量的类型
- 2 张量的阶
2.4.2 创建张量的指令
- 固定值张量
- 随机值张量
2.4.3 张量的变换
- 1 类型改变
- 2 形状改变
2.4.4 张量的数学运算

在编写 TensorFlow 程序时，程序传递和运算的主要目标是tf.Tensor

2.4.1 张量(Tensor)

TensorFlow 的张量就是一个 n 维数组，类型为tf.Tensor。Tensor具有以下两个重要的属性

type:数据类型
shape:形状(阶)

2.4.1.1 张量的类型

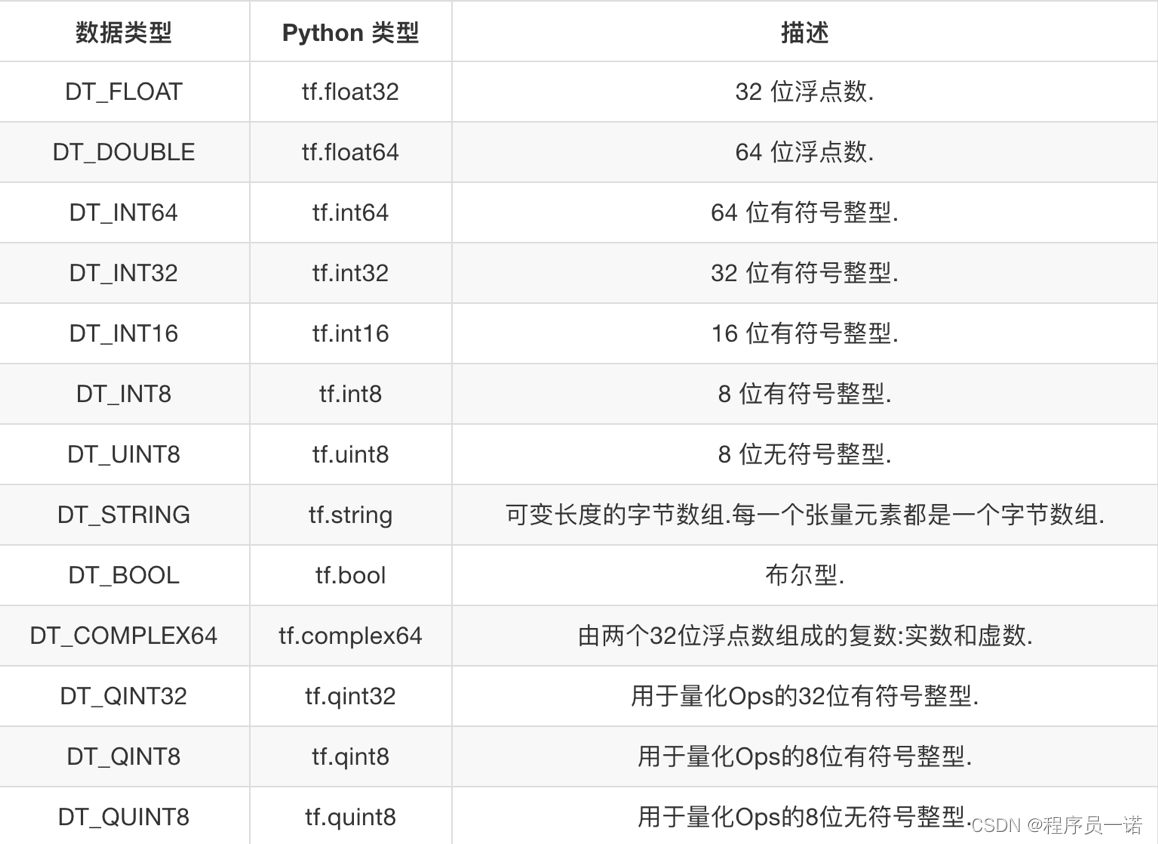
2.4.1.2 张量的阶

形状有0阶、1阶、2阶….

tensor1 = tf.constant(4.0)
tensor2 = tf.constant([1, 2, 3, 4])
linear_squares = tf.constant([[4], [9], [16], [25]], dtype=tf.int32)

print(tensor1.shape)


# 0维：()   1维：(10, )   2维：(3, 4)   3维：(3, 4, 5)

2.4.2 创建张量的指令

固定值张量

固定值张量

随机值张量

随机值张量

其它特殊的创建张量的op
tf.Variable
tf.placeholder

2.4.3 张量的变换

1 类型改变

类型变换

2 形状改变

TensorFlow的张量具有两种形状变换，动态形状和静态形状

tf.reshape
tf.set_shape

关于动态形状和静态形状必须符合以下规则

静态形状
转换静态形状的时候，1-D到1-D，2-D到2-D，不能跨阶数改变形状
对于已经固定的张量的静态形状的张量，不能再次设置静态形状
动态形状
tf.reshape()动态创建新张量时，张量的元素个数必须匹配

def tensor_demo():
    """
    张量的介绍
    :return:
    """
    a = tf.constant(value=30.0, dtype=tf.float32, name="a")
    b = tf.constant([[1, 2], [3, 4]], dtype=tf.int32, name="b")
    a2 = tf.constant(value=30.0, dtype=tf.float32, name="a2")
    c = tf.placeholder(dtype=tf.float32, shape=[2, 3, 4], name="c")
    sum = tf.add(a, a2, name="my_add")
    print(a, a2, b, c)
    print(sum)
    # 获取张量属性
    print("a的图属性：\n", a.graph)
    print("b的名字：\n", b.name)
    print("a2的形状：\n", a2.shape)
    print("c的数据类型：\n", c.dtype)
    print("sum的op:\n", sum.op)

    # 获取静态形状
    print("b的静态形状：\n", b.get_shape())

    # 定义占位符
    a_p = tf.placeholder(dtype=tf.float32, shape=[None, None])
    b_p = tf.placeholder(dtype=tf.float32, shape=[None, 10])
    c_p = tf.placeholder(dtype=tf.float32, shape=[3, 2])
    # 获取静态形状
    print("a_p的静态形状为：\n", a_p.get_shape())
    print("b_p的静态形状为：\n", b_p.get_shape())
    print("c_p的静态形状为：\n", c_p.get_shape())

    # 形状更新
    # a_p.set_shape([2, 3])
    # 静态形状已经固定部分就不能修改了
    # b_p.set_shape([10, 3])
    # c_p.set_shape([2, 3])

    # 静态形状已经固定的部分包括它的阶数，如果阶数固定了，就不能跨阶更新形状
    # 如果想要跨阶改变形状，就要用动态形状
    # a_p.set_shape([1, 2, 3])
    # 获取静态形状
    print("a_p的静态形状为：\n", a_p.get_shape())
    print("b_p的静态形状为：\n", b_p.get_shape())
    print("c_p的静态形状为：\n", c_p.get_shape())

    # 动态形状
    # c_p_r = tf.reshape(c_p, [1, 2, 3])
    c_p_r = tf.reshape(c_p, [2, 3])
    # 动态形状，改变的时候，不能改变元素的总个数
    # c_p_r2 = tf.reshape(c_p, [3, 1])
    print("动态形状的结果：\n", c_p_r)
    # print("动态形状的结果2：\n", c_p_r2)
    return None

2.4.4 张量的数学运算

算术运算符
基本数学函数
矩阵运算
reduce操作
序列索引操作

详细请参考: [

这些API使用，我们在使用的时候介绍，具体参考文档

2.5 变量OP

目标
说明变量op的特殊作用
说明变量op的trainable参数的作用
应用global_variables_initializer实现变量op的初始化
应用
无
内容预览
2.5.1 创建变量
2.5.2 使用tf.variable_scope()修改变量的命名空间

TensorFlow变量是表示程序处理的共享持久状态的最佳方法。变量通过 tf.Variable OP类进行操作。变量的特点：

存储持久化
可修改值
可指定被训练

2.5.1 创建变量

tf.Variable(initial_value=None,trainable=True,collections=None,name=None)
initial_value:初始化的值
trainable:是否被训练
collections：新变量将添加到列出的图的集合中collections，默认为[GraphKeys.GLOBAL_VARIABLES]，如果trainable是True变量也被添加到图形集合 GraphKeys.TRAINABLE_VARIABLES
变量需要显式初始化，才能运行值

def variable_demo():
    """
    变量的演示
    :return:
    """
    # 定义变量
    a = tf.Variable(initial_value=30)
    b = tf.Variable(initial_value=40)
    sum = tf.add(a, b)

    # 初始化变量
    init = tf.global_variables_initializer()

    # 开启会话
    with tf.Session() as sess:
        # 变量初始化
        sess.run(init)
        print("sum:\n", sess.run(sum))

    return None

2.5.2 使用tf.variable_scope()修改变量的命名空间

会在OP的名字前面增加命名空间的指定名字

with tf.variable_scope("name"):
    var = tf.Variable(name='var', initial_value=[4], dtype=tf.float32)
    var_double = tf.Variable(name='var', initial_value=[4], dtype=tf.float32)

<tf.Variable 'name/var:0' shape=() dtype=float32_ref>
<tf.Variable 'name/var_1:0' shape=() dtype=float32_ref>

TensorFlow介绍

说明TensorFlow的数据流图结构
应用TensorFlow操作图
说明会话在TensorFlow程序中的作用
应用TensorFlow实现张量的创建、形状类型修改操作
应用Variable实现变量op的创建
应用Tensorboard实现图结构以及张量值的显示
应用tf.train.saver实现TensorFlow的模型保存以及加载
应用tf.app.flags实现命令行参数添加和使用
应用TensorFlow实现线性回归

2.7 案例：实现线性回归

学习目标

目标
应用op的name参数实现op的名字修改
应用variable_scope实现图程序作用域的添加
应用scalar或histogram实现张量值的跟踪显示
应用merge_all实现张量值的合并
应用add_summary实现张量值写入文件
应用tf.train.saver实现TensorFlow的模型保存以及加载
应用tf.app.flags实现命令行参数添加和使用
应用reduce_mean、square实现均方误差计算
应用tf.train.GradientDescentOptimizer实现有梯度下降优化器创建
应用minimize函数优化损失
知道梯度爆炸以及常见解决技巧
应用
实现线性回归模型
内容预览
2.7.1 线性回归原理复习
2.7.2 案例：实现线性回归的训练
2.7.3 增加其他功能
- 1 增加变量显示
- 2 增加命名空间
- 3 模型的保存与加载
- 4 命令行参数使用

2.7.1 线性回归原理复习

根据数据建立回归模型，w1x1+w2x2+…..+b = y，通过真实值与预测值之间建立误差，使用梯度下降优化得到损失最小对应的权重和偏置。最终确定模型的权重和偏置参数。最后可以用这些参数进行预测。

2.7.2 案例：实现线性回归的训练

1 案例确定

假设随机指定100个点，只有一个特征
数据本身的分布为 y = 0.8 * x + 0.7

这里将数据分布的规律确定，是为了使我们训练出的参数跟真实的参数（即0.8和0.7）比较是否训练准确

2 API

运算

矩阵运算
tf.matmul(x, w)
平方
tf.square(error)
均值
tf.reduce_mean(error)

梯度下降优化

tf.train.GradientDescentOptimizer(learning_rate)
梯度下降优化
learning_rate:学习率，一般为0~1之间比较小的值
method:
- minimize(loss)
return:梯度下降op

3 步骤分析

1 准备好数据集：y = 0.8x + 0.7 100个样本
2 建立线性模型
随机初始化W1和b1
y = W·X + b，目标：求出权重W和偏置b
3 确定损失函数（预测值与真实值之间的误差）-均方误差
4 梯度下降优化损失：需要指定学习率（超参数）

4 实现完整功能

import tensorflow as tf
import os

def linear_regression():
    """
    自实现线性回归
    :return: None
    """
    # 1）准备好数据集：y = 0.8x + 0.7 100个样本
    # 特征值X, 目标值y_true
    X = tf.random_normal(shape=(100, 1), mean=2, stddev=2)
    # y_true [100, 1]
    # 矩阵运算 X（100， 1）* （1, 1）= y_true(100, 1)
    y_true = tf.matmul(X, [[0.8]]) + 0.7
    # 2）建立线性模型：
    # y = W·X + b，目标：求出权重W和偏置b
    # 3）随机初始化W1和b1
    weights = tf.Variable(initial_value=tf.random_normal(shape=(1, 1)))
    bias = tf.Variable(initial_value=tf.random_normal(shape=(1, 1)))
    y_predict = tf.matmul(X, weights) + bias
    # 4）确定损失函数（预测值与真实值之间的误差）-均方误差
    error = tf.reduce_mean(tf.square(y_predict - y_true))
    # 5）梯度下降优化损失：需要指定学习率（超参数）
    # W2 = W1 - 学习率*(方向)
    # b2 = b1 - 学习率*(方向)
    optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error)

    # 初始化变量
    init = tf.global_variables_initializer()
    # 开启会话进行训练
    with tf.Session() as sess:
        # 运行初始化变量Op
        sess.run(init)
        print("随机初始化的权重为%f， 偏置为%f" % (weights.eval(), bias.eval()))
        # 训练模型
        for i in range(100):
            sess.run(optimizer)
            print("第%d步的误差为%f，权重为%f， 偏置为%f" % (i, error.eval(), weights.eval(), bias.eval()))

    return None

6 变量的trainable设置观察

trainable的参数作用，指定是否训练

weight = tf.Variable(tf.random_normal([1, 1], mean=0.0, stddev=1.0), name="weights", trainable=False)

2.7.3 增加其他功能

增加命名空间
命令行参数设置

2 增加命名空间

是代码结构更加清晰，Tensorboard图结构清楚

with tf.variable_scope("lr_model"):

def linear_regression():
    # 1）准备好数据集：y = 0.8x + 0.7 100个样本
    # 特征值X, 目标值y_true
    with tf.variable_scope("original_data"):
        X = tf.random_normal(shape=(100, 1), mean=2, stddev=2, name="original_data_x")
        # y_true [100, 1]
        # 矩阵运算 X（100， 1）* （1, 1）= y_true(100, 1)
        y_true = tf.matmul(X, [[0.8]], name="original_matmul") + 0.7
    # 2）建立线性模型：
    # y = W·X + b，目标：求出权重W和偏置b
    # 3）随机初始化W1和b1
    with tf.variable_scope("linear_model"):
        weights = tf.Variable(initial_value=tf.random_normal(shape=(1, 1)), name="weights")
        bias = tf.Variable(initial_value=tf.random_normal(shape=(1, 1)), name="bias")
        y_predict = tf.matmul(X, weights, name="model_matmul") + bias
    # 4）确定损失函数（预测值与真实值之间的误差）-均方误差
    with tf.variable_scope("loss"):
        error = tf.reduce_mean(tf.square(y_predict - y_true), name="error_op")
    # 5）梯度下降优化损失：需要指定学习率（超参数）
    # W2 = W1 - 学习率*(方向)
    # b2 = b1 - 学习率*(方向)
    with tf.variable_scope("gd_optimizer"):
        optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01, name="optimizer").minimize(error)

    # 2）收集变量
    tf.summary.scalar("error", error)
    tf.summary.histogram("weights", weights)
    tf.summary.histogram("bias", bias)

    # 3）合并变量
    merge = tf.summary.merge_all()

    # 初始化变量
    init = tf.global_variables_initializer()
    # 开启会话进行训练
    with tf.Session() as sess:
        # 运行初始化变量Op
        sess.run(init)
        print("随机初始化的权重为%f， 偏置为%f" % (weights.eval(), bias.eval()))
        # 1）创建事件文件
        file_writer = tf.summary.FileWriter(logdir="./summary", graph=sess.graph)
        # 训练模型
        for i in range(100):
            sess.run(optimizer)
            print("第%d步的误差为%f，权重为%f， 偏置为%f" % (i, error.eval(), weights.eval(), bias.eval()))
            # 4）运行合并变量op
            summary = sess.run(merge)
            file_writer.add_summary(summary, i)

    return None

3 模型的保存与加载

tf.train.Saver(var_list=None,max_to_keep=5)
保存和加载模型（保存文件格式：checkpoint文件）
var_list:指定将要保存和还原的变量。它可以作为一个dict或一个列表传递.
max_to_keep：指示要保留的最近检查点文件的最大数量。创建新文件时，会删除较旧的文件。如果无或0，则保留所有检查点文件。默认为5（即保留最新的5个检查点文件。）

使用

例如：
指定目录+模型名字
saver.save(sess, '/tmp/ckpt/test/myregression.ckpt')
saver.restore(sess, '/tmp/ckpt/test/myregression.ckpt')

如要判断模型是否存在，直接指定目录

checkpoint = tf.train.latest_checkpoint("./tmp/model/")

saver.restore(sess, checkpoint)

4 命令行参数使用

1、
2、 tf.app.flags.,在flags有一个FLAGS标志，它在程序中可以调用到我们

前面具体定义的flag_name

3、通过tf.app.run()启动main(argv)函数

# 定义一些常用的命令行参数




# 训练步数


tf.app.flags.DEFINE_integer("max_step", 0, "训练模型的步数")


# 定义模型的路径


tf.app.flags.DEFINE_string("model_dir", " ", "模型保存的路径+模型名字")



# 定义获取命令行参数


FLAGS = tf.app.flags.FLAGS



# 开启训练




# 训练的步数（依据模型大小而定）


for i in range(FLAGS.max_step):
     sess.run(train_op)

完整代码

import tensorflow as tf
import os

tf.app.flags.DEFINE_string("model_path", "./linear_regression/", "模型保存的路径和文件名")
FLAGS = tf.app.flags.FLAGS


def linear_regression():
    # 1）准备好数据集：y = 0.8x + 0.7 100个样本
    # 特征值X, 目标值y_true
    with tf.variable_scope("original_data"):
        X = tf.random_normal(shape=(100, 1), mean=2, stddev=2, name="original_data_x")
        # y_true [100, 1]
        # 矩阵运算 X（100， 1）* （1, 1）= y_true(100, 1)
        y_true = tf.matmul(X, [[0.8]], name="original_matmul") + 0.7
    # 2）建立线性模型：
    # y = W·X + b，目标：求出权重W和偏置b
    # 3）随机初始化W1和b1
    with tf.variable_scope("linear_model"):
        weights = tf.Variable(initial_value=tf.random_normal(shape=(1, 1)), name="weights")
        bias = tf.Variable(initial_value=tf.random_normal(shape=(1, 1)), name="bias")
        y_predict = tf.matmul(X, weights, name="model_matmul") + bias
    # 4）确定损失函数（预测值与真实值之间的误差）-均方误差
    with tf.variable_scope("loss"):
        error = tf.reduce_mean(tf.square(y_predict - y_true), name="error_op")
    # 5）梯度下降优化损失：需要指定学习率（超参数）
    # W2 = W1 - 学习率*(方向)
    # b2 = b1 - 学习率*(方向)
    with tf.variable_scope("gd_optimizer"):
        optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01, name="optimizer").minimize(error)

    # 2）收集变量
    tf.summary.scalar("error", error)
    tf.summary.histogram("weights", weights)
    tf.summary.histogram("bias", bias)

    # 3）合并变量
    merge = tf.summary.merge_all()

    # 初始化变量
    init = tf.global_variables_initializer()

    # 开启会话进行训练
    with tf.Session() as sess:
        # 运行初始化变量Op
        sess.run(init)
        # 未经训练的权重和偏置
        print("随机初始化的权重为%f， 偏置为%f" % (weights.eval(), bias.eval()))
        # 当存在checkpoint文件，就加载模型

        # 1）创建事件文件
        file_writer = tf.summary.FileWriter(logdir="./summary", graph=sess.graph)
        # 训练模型
        for i in range(100):
            sess.run(optimizer)
            print("第%d步的误差为%f，权重为%f， 偏置为%f" % (i, error.eval(), weights.eval(), bias.eval()))
            # 4）运行合并变量op
            summary = sess.run(merge)
            file_writer.add_summary(summary, i)

    return None


def main(argv):
    print("这是main函数")
    print(argv)
    print(FLAGS.model_path)
    linear_regression()

if __name__ == "__main__":
    tf.app.run()

作业：将面向过程改为面向对象

参考代码

# 用tensorflow自实现一个线性回归案例





# 定义一些常用的命令行参数




# 训练步数


tf.app.flags.DEFINE_integer("max_step", 0, "训练模型的步数")


# 定义模型的路径


tf.app.flags.DEFINE_string("model_dir", " ", "模型保存的路径+模型名字")

FLAGS = tf.app.flags.FLAGS

class MyLinearRegression(object):
    """
    自实现线性回归
    """
    def __init__(self):
        pass

    def inputs(self):
        """
        获取特征值目标值数据数据
        :return:
        """
        x_data = tf.random_normal([100, 1], mean=1.0, stddev=1.0, name="x_data")
        y_true = tf.matmul(x_data, [[0.7]]) + 0.8

        return x_data, y_true

    def inference(self, feature):
        """
        根据输入数据建立模型
        :param feature:
        :param label:
        :return:
        """
        with tf.variable_scope("linea_model"):
            # 2、建立回归模型，分析别人的数据的特征数量--->权重数量， 偏置b
            # 由于有梯度下降算法优化，所以一开始给随机的参数，权重和偏置
            # 被优化的参数，必须得使用变量op去定义
            # 变量初始化权重和偏置
            # weight 2维[1, 1]    bias [1]
            # 变量op当中会有trainable参数决定是否训练
            self.weight = tf.Variable(tf.random_normal([1, 1], mean=0.0, stddev=1.0),
                                 name="weights")

            self.bias = tf.Variable(0.0, name='biases')

            # 建立回归公式去得出预测结果
            y_predict = tf.matmul(feature, self.weight) + self.bias

        return y_predict

    def loss(self, y_true, y_predict):
        """
        目标值和真实值计算损失
        :return: loss
        """
        # 3、求出我们模型跟真实数据之间的损失
        # 均方误差公式
        loss = tf.reduce_mean(tf.square(y_true - y_predict))

        return loss

    def merge_summary(self, loss):

        # 1、收集张量的值
        tf.summary.scalar("losses", loss)

        tf.summary.histogram("w", self.weight)
        tf.summary.histogram('b', self.bias)

        # 2、合并变量
        merged = tf.summary.merge_all()

        return merged

    def sgd_op(self, loss):
        """
        获取训练OP
        :return:
        """
        # 4、使用梯度下降优化器优化
        # 填充学习率：0 ~ 1    学习率是非常小，
        # 学习率大小决定你到达损失一个步数多少
        # 最小化损失
        train_op = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

        return train_op

    def train(self):
        """
        训练模型
        :param loss:
        :return:
        """

        g = tf.get_default_graph()

        with g.as_default():

            x_data, y_true = self.inputs()

            y_predict = self.inference(x_data)

            loss = self.loss(y_true, y_predict)

            train_op = self.sgd_op(loss)

            # 收集观察的结果值
            merged = self.merge_summary(loss)

            saver = tf.train.Saver()

            with tf.Session() as sess:

                sess.run(tf.global_variables_initializer())

                # 在没训练，模型的参数值
                print("初始化的权重：%f, 偏置：%f" % (self.weight.eval(), self.bias.eval()))

                # 开启训练
                # 训练的步数（依据模型大小而定）
                for i in range(FLAGS.max_step):

                    sess.run(train_op)

                    # 生成事件文件，观察图结构
                    file_writer = tf.summary.FileWriter("./tmp/summary/", graph=sess.graph)

                    print("训练第%d步之后的损失:%f, 权重：%f, 偏置：%f" % (
                        i,
                        loss.eval(),
                        self.weight.eval(),
                        self.bias.eval()))

                    # 运行收集变量的结果
                    summary = sess.run(merged)

                    # 添加到文件
                    file_writer.add_summary(summary, i)


if __name__ == '__main__':
    lr = MyLinearRegression()
    lr.train()