面试经典150题【111-120】

六道位运算，四道二维dp

67.二进制求和

class Solution {
    public String addBinary(String a, String b) {
        StringBuilder str = new StringBuilder();
        int carry = 0;
        for (int i = a.length() - 1, j = b.length() - 1; i >= 0 || j >= 0; i--, j--) {
            int sum = carry;
            sum += i >= 0 ? a.charAt(i) - '0' : 0;
            sum += j >= 0 ? b.charAt(j) - '0' : 0;
            str.append(sum % 2);
            carry = sum / 2;
        }
        // 最后一位还没加
        if (carry == 1)
            str.append(carry);
        return str.reverse().toString();
    }
}

从后往前一位一位算，每一位为sum(进位，a,b)。

190.颠倒二进制位

颠倒给定的 32 位无符号整数的二进制位。

public class Solution {
    // you need treat n as an unsigned value
    public int reverseBits(int n) {
        int ans = 0;
        for (int i = 0; i < 32; i++) {
            ans |= (n & 1) << (31 - i);
            n = n >>> 1;
        }
        return ans;
    }
}

二进制的一些处理方法。 ans |= (n & 1) << (31 - i) 对某一位进行填充。

191.位1的个数

n = n&(n-1) 将n的最后一个1给消除掉
n =100
n-1 = 011
则n &(n-1) = 000

class Solution {
    public int hammingWeight(int n) {
        int ans=0;
        while(n!=0){
            n = n&(n-1);
            ans++;
        }
        return ans;
    }
}

136.只出现一次的数字

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。
所有元素依次亦或即可

137.只出现一次的数字II

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。

class Solution {
    public int singleNumber(int[] nums) {
        int[] count=new int[32];
        int res=0;
        for(int i=0;i<nums.length;i++){
            for(int j=0;j<32;j++){
                count[j] += nums[i]&1;
                nums[i] >>>=1;
            }
        }
        for(int i=0;i<32;i++){
            res |= (count[i]%3)<<i;
        }
        return res;

    }
}

定义一个32位长度的数组，将每个数字的二进制位填入数组中，比如101，填入数组的第一位和第三位。
则对于2,2，2,3这种。10,10,10,101
count数组的内容为 1,3,1
然后所有的内容都对3取余，这样就可以消除所有的出现三次的数字
count的内容为1,0，1.
就可以筛选出3来了。

201.数字范围按位与

给你两个整数 left 和 right ，表示区间 [left, right] ，返回此区间内所有数字 按位与 的结果（包含 left 、right 端点）。
按位与， 0&0=0, 0&1=0, 1&1=1

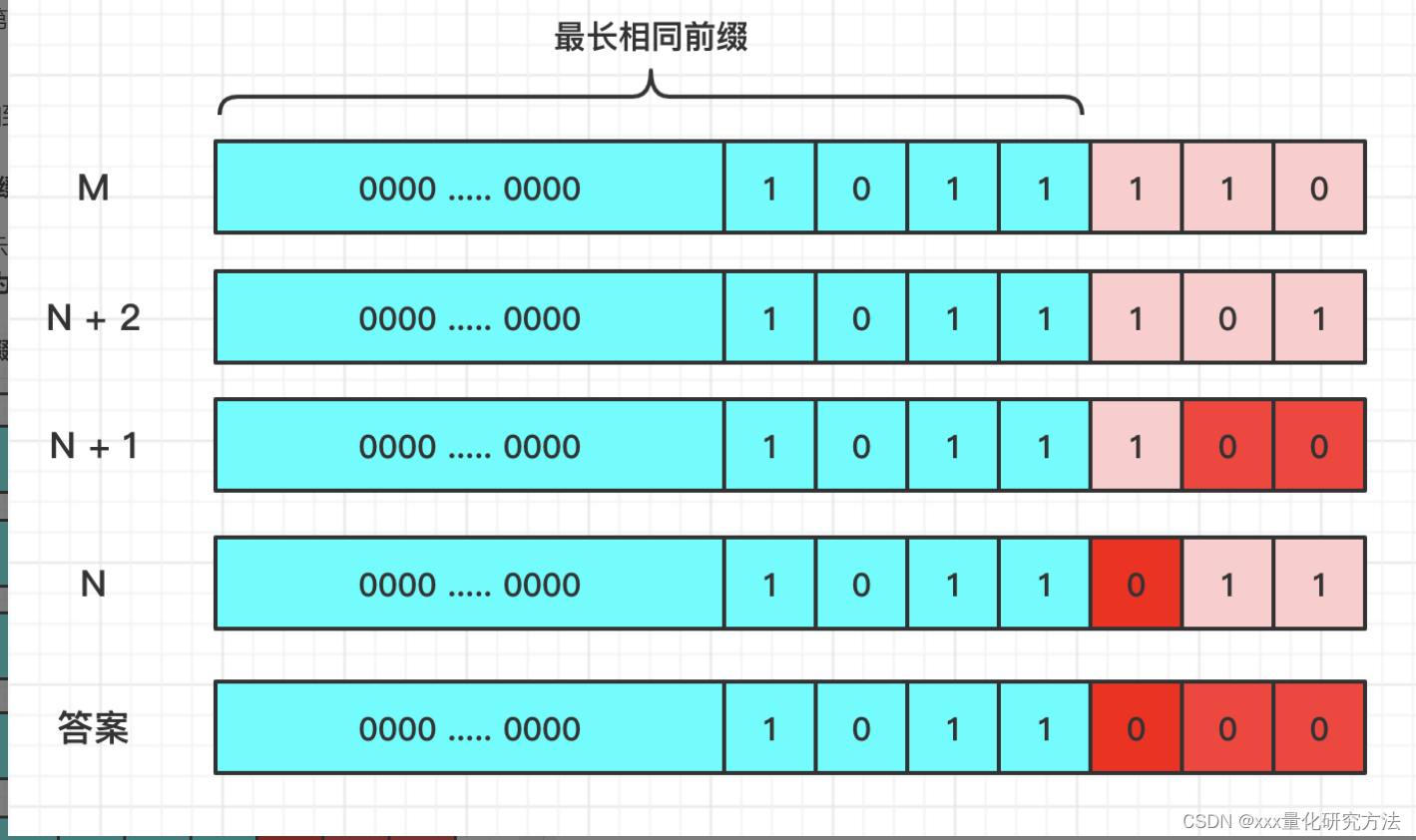
所以其本质就是寻找最长的相同前缀。
M是很大的，N是很小的。我不停的消除掉M最右边的1，直到把红色的部分全部消除完。这样M就会小于等于N了。

public int rangeBitwiseAnd(int left, int right) {
        while(left<right){
            right = right & (right-1);
        }
        return right;

    }

5.最长回文子串

最标准的就是中心扩散，这样是O(N^2)，也可以用二维数组记录一下状态，减少一些搜索量。

class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 2) {
            return s;
        }
        int strLen = s.length();
        int maxStart = 0;  //最长回文串的起点
        int maxEnd = 0;    //最长回文串的终点
        int maxLen = 1;  //最长回文串的长度
        boolean[][] dp=new boolean[strLen][strLen];

        for(int j=0;j<strLen;j++){
            for(int i=0;i<j;i++){
                if(s.charAt(i)==s.charAt(j) &&(j-i<=2 || dp[i+1][j-1])){
                    dp[i][j]=true;
                    if(j-i+1 >maxLen){
                        maxLen=j-i+1;
                        maxStart=i;
                        maxEnd=j;
                    }
                }
            }
        }
        return s.substring(maxStart,maxEnd+1);

    }
}

97.交错字符串

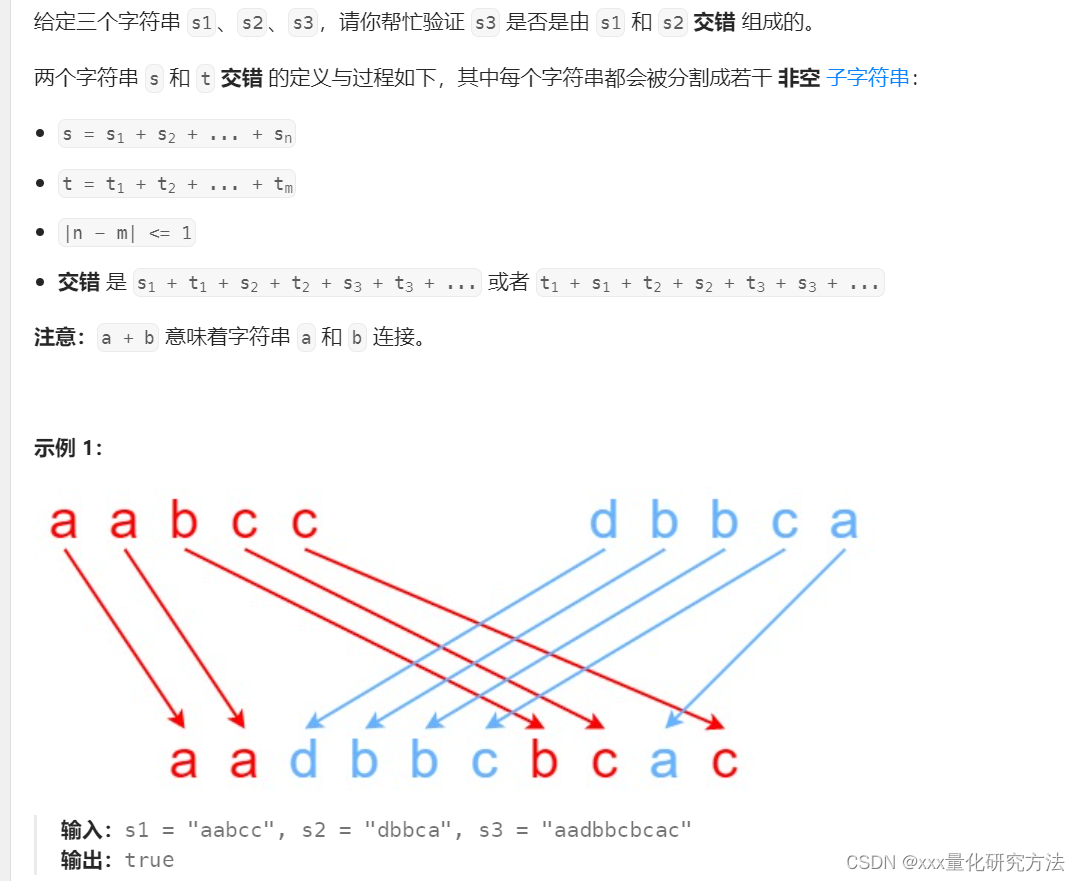
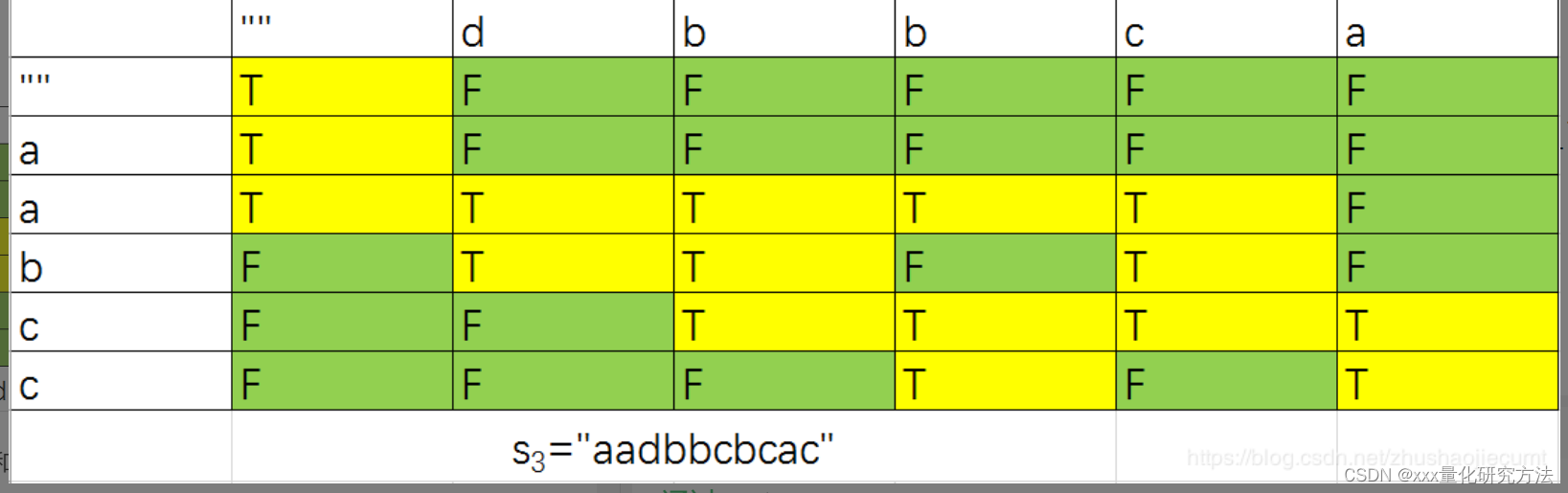
dp[i][j] 表示 由s1的前i个字符 和 s2 的前j个字符，能不能组成s3的前 i+j 个字符。
建立数组的时候长度要加一，不然直接dp[0][0]为s1前1个字符和s2前1个字符能不能组成s3的前2个字符，这显然是不合适的。
如果空出来第一列和第一行就很合适了。比如就是说s1的0个字符和s2的N个字符，只需要考虑s2即可。

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        if(s1.length()+s2.length() != s3.length()) return false;
        boolean[][] ans = new boolean[s1.length() + 1][s2.length() + 1];
        ans[0][0] = true;
        for (int i = 1; i < s1.length() + 1; i++) {
            ans[i][0] = ans[i - 1][0] && (s3.charAt(i - 1) == s1.charAt(i - 1));
        }
        for (int j = 1; j < s2.length() + 1; j++) {
            ans[0][j] = ans[0][j - 1] && (s3.charAt(j - 1) == s2.charAt(j - 1));
        }
        for (int i = 1; i < s1.length() + 1; i++) {
            for (int j = 1; j < s2.length() + 1; j++) {
                ans[i][j] = (ans[i - 1][j] && (s3.charAt(i + j - 1) == s1.charAt(i - 1)))
                        || (ans[i][j - 1] && (s3.charAt(i + j - 1) == s2.charAt(j - 1)));
            }
        }
        return ans[s1.length()][s2.length()];

    }
}

72.编辑距离

dp[i][j]代表将word1的前i个字符转换为word2的前j个字符所需要的转换次数。
其中，dp[i-1][j-1] 表示替换操作，dp[i-1][j] 表示删除操作，dp[i][j-1] 表示插入操作。
注意，针对第一行，第一列要单独考虑，我们引入 ‘’ 下图所示：

    public int minDistance(String word1, String word2) {
        int[][] dp=new int[word1.length()+1][word2.length()+1];
        for(int i=0;i<word1.length()+1;i++){
            dp[i][0]=i;
        }
        for(int j=0;j<word2.length()+1;j++){
            dp[0][j]=j;
        }
        for(int i=1;i<word1.length()+1;i++){
            for(int j=1;j<word2.length()+1;j++){
                if(word1.charAt(i-1)==word2.charAt(j-1)) dp[i][j]=dp[i-1][j-1];
                //分别对应 添加，删除和替换三种情况
                else dp[i][j]=Math.min(Math.min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;

            }
        }
        return dp[word1.length()][word2.length()];
    }

221.最大正方形

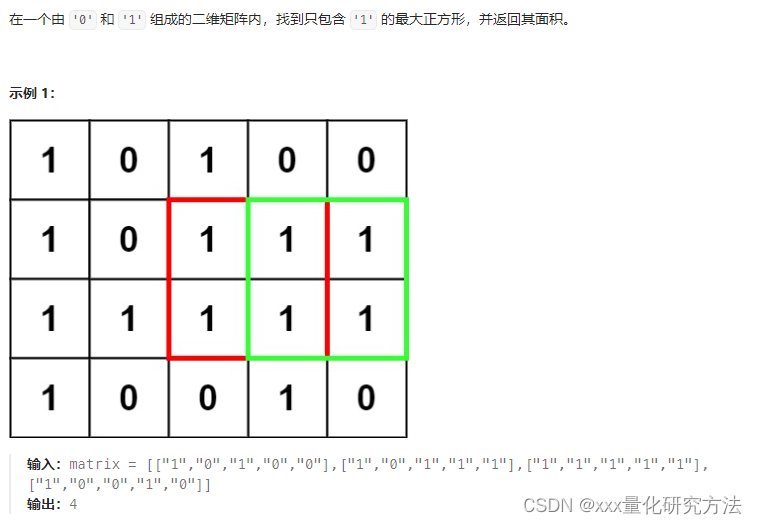
dp[i][j]表示 以(i,j) 为右下角，能形成的最大的矩阵。

class Solution {
    public int maximalSquare(char[][] matrix) {
        int ans=0;
        int[][] dp=new int[matrix.length+1][matrix[0].length+1];
        for(int i=1;i< matrix.length+1;i++){
            for(int j=1;j<matrix[0].length+1;j++){
                if(matrix[i-1][j-1]=='1'){
                    dp[i][j]=1+Math.min(dp[i-1][j-1],Math.min(dp[i][j-1],dp[i-1][j]));
                    ans=Math.max(ans,dp[i][j]);
                    
                }
            }
        }
        return ans*ans;

    }
}

这边二维dp，特别容易长度加一
int[][] dp=new int[matrix.length+1][matrix[0].length+1];
第一行和第一列用来缓冲，1 到 length 这些索引才是符合题意的，因为要兼容第二行的 i-1,j-1之类的需求。