相关题目: 210 课程表2
【力扣hot100】207 课程表(c++、python)解析
-
- 1.官方题解:
-
- 1.1深搜
- c++版本
- python版本
- 1.2广搜
- c++版本
1.官方题解:
这是一题经典的「拓扑排序」问题
给定一个包含 n 个节点的有向图 G,我们给出它的节点编号的一种排列,如果满足:对于图 G 中的任意一条有向边 (u,v),u 在排列中都出现在 v 的前面那么称该排列是图 G 的「拓扑排序」
*1.如果图 G 中存在环(即图 G 不是「有向无环图」),那么图 G 不存在拓扑排序。这是因为假设图中存在环 “x1,x2,…,„,í,那么 x1在排列中必须出现在 xn 的前面,但 xn同时也必须出现在 x1的前面,因此不存在一个满足要求的排列,也就不存在拓扑排序
*2.如果图 G 是有向无环图,那么它的拓扑排序可能不止一种。举一个最极端的例子,如果图 G 值包含n个节点却没有任何边,那么任意一种编号的排列都可以作为拓扑排序
有了上述的简单分析,我们就可以将本题建模成一个求拓扑排序的问题了
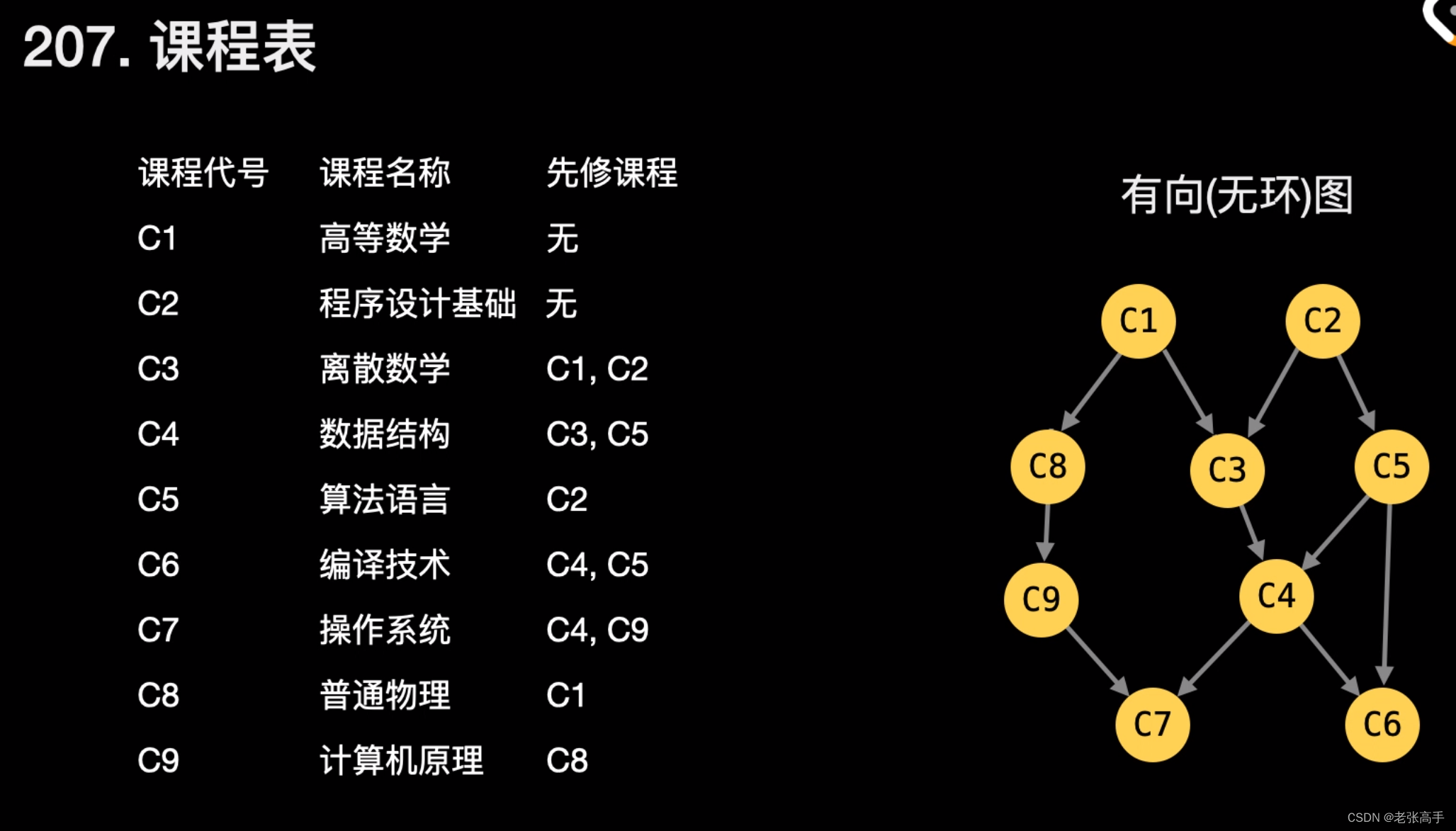
我们将每一门课看成一个节点
如果想要学习课程 A 之前必须完成课程 B,那么我们从 B 到 A 连接一条有向边。这样以来,在拓扑排序中,B一定出现在 A 的前面。

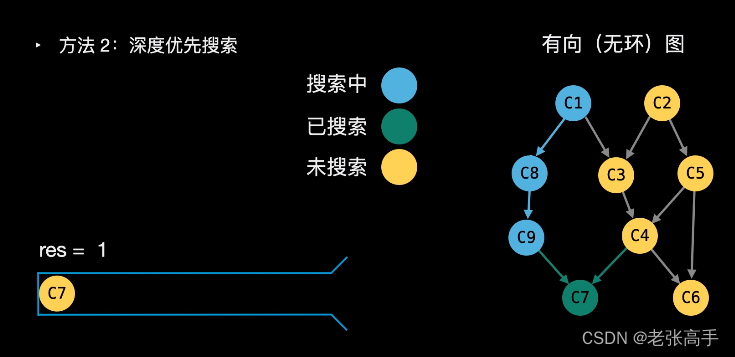
1.1深搜
从出度思考(从后往前排序), 出度为0的节点在拓扑排序中一定排在后面, 然后删除和该节点对应的边, 迭代寻找出度为0的节点
我们可以将深度优先搜索的流程与拓扑排序的求解联系起来,用一个栈来存储所有已经搜索完成的节点。
对于一个节点 u,如果它的所有相邻节点都已经搜索完成,那么在搜索回溯到u的时候,u本身也会变成一个已经搜索完成的节点。这里的「相邻节点」指的是从u出发通过一条有向边可以到达的所有节点。
假设我们当前搜索到了节点u,如果它的所有相邻节点都已经搜索完成,那么这些节点都已经在栈中了,此时我们就可以把u入栈。可以发现,如果我们从栈顶往栈底的顺序看,由于 u 处于栈顶的位置,那么 u 出现在所有 u 的相邻节点的前面。因此对于 u 这个节点而言,它是满足拓扑排序的要求的。
这样以来,我们对图进行一遍深度优先搜索。当每个节点进行回溯的时候,我们把该节点放入栈中。最终从栈顶到栈底的序列就是一种拓扑排序。

c++版本
//一个二维向量,用于表示课程之间的依赖关系,每个元素`edges[u]`表示课程`u`的先修课程列表。
//`visited`:用于标记课程的访问状态,0表示未访问,1表示正在访问,2表示已访问。
//`valid`:表示当前的课程安排是否有效,初始值为`true`
class Solution{
private:
vector<vector<int>> edges;
vector<int> visited;
bool valid = true;
public:
//用于从课程`u`开始进行深度优先遍历。在遍历过程中,会对课程进行标记,同时检查是否存在环路。若存在环路,则将`valid`设为`false`,表示无法完成所有课程。
void dfs(int u)
{
visited[u] = 1;//从课程`u`开始进行深度优先遍历
for(int v:edges[u])//遍历课程u的先修课程
{
if(visited[v] == 0)//如果有没访问的先修课程