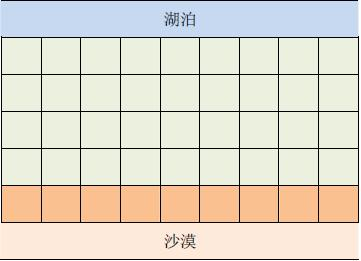
在一个遥远的国度,一侧是风景秀美的湖泊,另一侧则是漫无边际的沙漠。该国的行政区划十分特殊,刚好构成一个 N 行 M 列的矩形,如上图所示,其中每个格子都代表一座城市,每座城市都有一个海拔高度。
为了使居民们都尽可能饮用到清澈的湖水,现在要在某些城市建造水利设施。水利设施有两种,分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。因此,只有与湖泊毗邻的第 1 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差,将湖水从高处向低处输送。故一座城市能建造输水站的前提,是存在比它海拔更高且拥有公共边的相邻城市,已经建有水利设施。
由于第 N 行的城市靠近沙漠,是该国的干旱区,所以要求其中的每座城市都建有水利设施。那么,这个要求能否满足呢?如果能,请计算少建造几个蓄水厂;如果不能,求干旱区中不可能建有水利设施的城市数目。
输入格式:
输入的每行中两个数之间用一个空格隔开。
输入的第一行是两个正整数 N 和 M,表示矩形的规模;
接下来 N 行,每行 M 个正整数,依次代表每座城市的海拔高度。
输出格式:
输出有两行。
如果能满足要求,输出的第一行是整数 1 ,第二行是一个整数,代表最少建造几个蓄水厂;
如果不能满足要求,输出的第一行是整数 0 ,第二行是一个整数,代表有几座干旱区中的城市不可能建有水利设施。
输入样例1:
2 5
9 1 5 4 3
8 7 6 1 2
输出样例1:
1
1
样例说明1:
只需要在海拔为 9 的那座城市中建造蓄水厂,即可满足要求。
输入样例2:
3 6
8 4 5 6 4 4
7 3 4 3 3 3
3 2 2 1 1 2
输出样例2:
1
3
样例说明2:
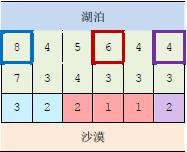
上图中,在 3 个粗线框出的城市中建造蓄水厂,可以满足要求。以这 3 个蓄水厂为源头在干旱区中建造的输水站分别用 3 种颜色标出。当然,建造方法可能不唯一。
数据范围
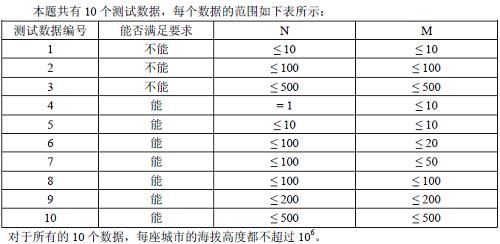
题目大意:
有公共边的两个点,只能从大往小走,最上面都可以是起始点。
问能不能把最下面一排都走到?
思路:
从最上面一排开始跑,记录每个点能跑到的最下面一排左边界和右边界。
方法:
用记忆搜标记每个走到的点能到的最下面一排左边界和右边界。
当再次跑到此点时直接读取数值。
核心记忆搜代码:
void dfs(ll x ,ll y){//现在到哪个点 vis[x][y]=1;//标记此点已经来过 for(ll i = 0 ; i < 4 ; i ++){ ll tx = x + dir[i][0]; ll ty = y + dir[i][1]; //下一个点不能走就直接跳过 if(tx < 1 || ty < 1 || tx > n || ty > m || v[x][y] <= v[tx][ty])continue; if(!vis[tx][ty])dfs(tx,ty);//继续搜没标记过的点 L[x][y] = min(L[x][y],L[tx][ty]);//记录此点能到的最小左端点 R[x][y] = max(R[x][y],R[tx][ty]);//记录此点能到的最大右端点 } }
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define endl "\n"
const ll N = 5e2+7;
ll n,m;
ll v[N][N],L[N][N],R[N][N];//记录此点高度,记录此点能到的最小左端点,记录此点能到的最大右端点
bool vis[N][N];
ll dir[4][2]={0,1,1,0,0,-1,-1,0};
void dfs(ll x ,ll y){//现在到哪个点
vis[x][y]=1;//标记此点已经来过
for(ll i = 0 ; i < 4 ; i ++){
ll tx = x + dir[i][0];
ll ty = y + dir[i][1];
//下一个点不能走就直接跳过
if(tx < 1 || ty < 1 || tx > n || ty > m || v[x][y] <= v[tx][ty])continue;
if(!vis[tx][ty])dfs(tx,ty);//继续搜没标记过的点
L[x][y] = min(L[x][y],L[tx][ty]);//记录此点能到的最小左端点
R[x][y] = max(R[x][y],R[tx][ty]);//记录此点能到的最大右端点
}
}
void solve(){
cin >> n >> m;
memset(L,0x3f,sizeof L);
memset(vis,0,sizeof vis);
for(ll i = 1 ; i <= m ; i ++)
L[n][i]=R[n][i]=i;
for(ll i = 1 ; i <= n ; i ++)
for(ll j = 1 ; j <= m ; j ++)
cin >> v[i][j];
ll cnt = 0 ,sum = 0;
for(ll i = 1 ; i <= m ; i ++)
if(vis[1][i])continue;
else dfs(1,i);
for(ll i = 1 ; i <= m ; i ++)//看最后一排是否有没有被连接的城市
if(!vis[n][i])sum++;
if(sum){//如果最下面一排不能全部被连接到
cout << 0 << endl << sum << endl;
return;
}
ll l = 1,r;
while(l <= m){//拼接能让最后一排都连接所需要的最少点
r=0;
for(ll i = 1 ; i <= m ; i ++)
if(L[1][i] <= l)r=max(r,R[1][i]);
cnt++;
l=r+1;
}
cout << 1 << endl << cnt << endl;
return ;
}
int main(){
ll t=1;//cin >> t;
while(t--)solve();
return 0;
}