第一个对完全隐私保护建模的方案,基于账户模型,要求交易双方都在线。
角色分类
中央银行
B
B
B:负责发行数字货币和货币政策,但不控制用户账户的状态,没有能力对交易的发送者或接收者进行去匿名化或披露与特定交易相关的转移价值,并且不负责执行支付的监管规则。
维护者
M
J
M_J
MJ:如商业银行和金融机构。负责验证交易和进行监管合规的各种审计操作,它们之间共享系统状态,且负责在用户发布交易时不断更新系统状态。所有的维护者的集合时公开的,只要敌手控制的维护者少于一定阈值,该系统就满足安全性。每个维护者都持有自己的账本(存有注册信息和交易信息)。
本方案中
- 所有维护者的数量为 ∣ M ∣ = D |\mathbb{M}| = D ∣M∣=D,设定了两个需要一定数量的维护者参与的门限阈值 α \alpha α(用于交易验证)和 β \beta β(用于执行审计协议)。
- 拥有两对ElGamal门限加密密钥对 ( p k 1 , j , s k 1 , j ) (pk_{1,j},sk_{1,j}) (pk1,j,sk1,j)和 ( p k 1 , j , s k 1 , j ) (pk_{1,j},sk_{1,j}) (pk1,j,sk1,j)。
用户
U
U
U:作为交易的发送方或接收方。
本方案中
- 拥有一对公私钥 ( p k U , s k U ) (pk_U,sk_U) (pkU,skU)。
- 用于生成每笔交易tag=
T
T
T的私钥
a
a
a
交易过程
下图是用户在一笔交易中的状态变化过程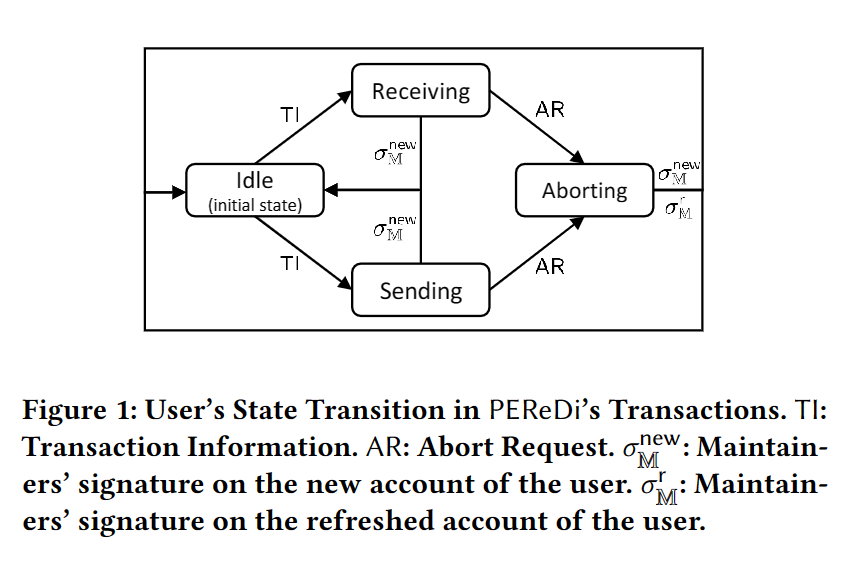
- Idle:惰态,用户交易之前的初始状态,发起交易的时候会发送交易信息 TI(包含用户的新盲签名账户)给所有维护者。发送交易之后,用户的状态将会更新为 Receiving/Sending。
- Receiving/Sending:处于该状态的时候,会自动忽略掉环境命令(生成新发送交易/接收交易,接收发行货币等等),也就是必须等上一笔交易完成,才能进行下一笔。当从此状态返回为 **Idle **状态时,代表一笔交易结束。结束有两种情况
- Successful:即,交易成功,交易双方使用了满足规范的新账户,并且维护者们也收到了双方有效的交易信息(TI)。用户收到至少门限个维护人员的盲签名后,解盲并在新账户上聚合出新的签名,最后更改自己的状态,至此就可以开启下一笔交易。
- Pending:也就是交易双方没有收到足够数量的盲签名,在收到 AR 中止请求(包含)的时候一直处于 Receiving/Sending 状态。用户在收到环境命令-中止交易 AR(包含用户重新刷新盲签名的账户)后,用户向维护者发送 AR。此时用户的状态切换为 Aborting
- if 至少门限个维护者收到交易双方的 TI 对并存到了各自的账本里,此时维护者就会忽略掉重新刷新的账户,并且给用户发送他们自己的签名(为了用户的新账户),然后用户用这些盲签名,解盲,在新的账户聚合出签名。最后账户切换为 Idle。
- else 维护者们对重随机的账户签名,并标记交易为中止,忽略掉新账户。用户用盲签名,解盲,在重随机账户上聚合出签名,最后账户切换为 Idle。
协议流程
初始化
主要是需要确保中央银行、维护人员都完成初始化,即激活在线。参与者们各自为每个方案的密码机制生成公私钥对。公钥会被保存在公钥目录中,该目录在需要的时候可以被获取到。用户会持有公私钥对以及一把私钥
a
a
a(用于标签生成)。
维护者的数量为
D
D
D,两个门限阈值
α
\alpha
α(用于交易验证)和
β
\beta
β(用于执行审计协议)
用户注册
即用户通过与维护者交互得到一个含有维护者签名的初始账户,便于进行第一次交易。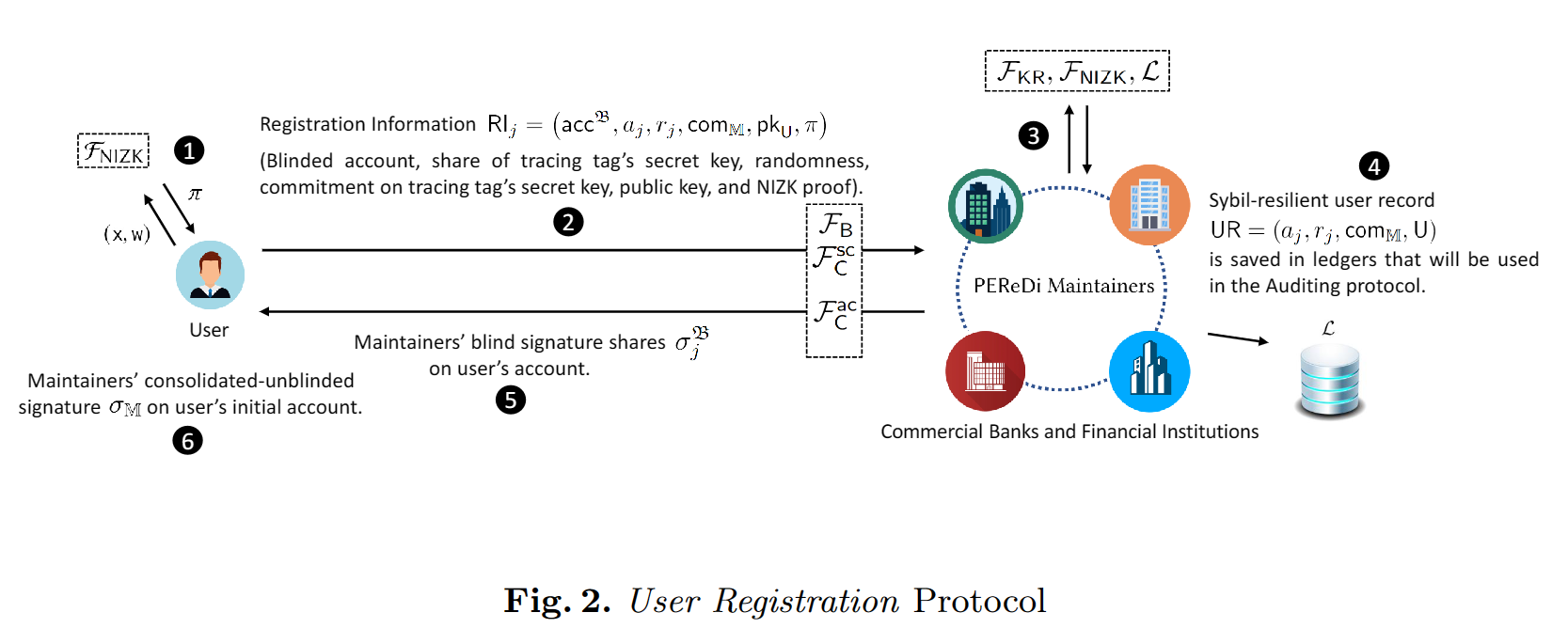
- 初始化:用户初始化自己的状态为 **Idle,**接着初始化注册协议,调用门限盲签名算法TBS获取带有盲签名的账户
a
c
c
B
acc^{\mathfrak{B}}
accB(账户的内容大致有
a
c
c
=
(
B
,
S
,
R
,
s
k
U
,
a
x
,
a
)
acc = (B,S,R,sk_U,a^x,a)
acc=(B,S,R,skU,ax,a),
B
,
S
,
R
,
x
B,S,R,x
B,S,R,x,分别代表余额,发送总值,接收总值和交易计数器,它们初始的时候都会被置为0),计算注册信息,
R
I
j
=
(
a
c
c
B
ˉ
,
a
j
,
r
j
,
c
o
m
M
,
p
k
U
,
π
)
\mathsf{RI}_j=(\mathsf{acc}^{\bar{\mathfrak{B}}},a_j,r_j,\mathsf{com}_{\mathbb{M}},\mathsf{pk}_{\mathbf{U}},\pi)
RIj=(accBˉ,aj,rj,comM,pkU,π)
- 对 a a a进行秘密分享得到 { a j } j = 1 \{a_j\}_{j=1} {aj}j=1并得到 a a a的承诺 c o m j ~ = g a j ⋅ h r j \tilde{\mathsf{com}_j}=g^{a_j}\cdot h^{r_j} comj~=gaj⋅hrj, c o m M = { c o m j ~ } j = 1 D com_{\mathbb{M}} = \{\tilde{\mathsf{com}_j}\}^D_{j=1} comM={comj~}j=1D。
- 证明:接着用户需要调用非交互式零知识证明生成 Proof
π
\pi
π,证明自己确实诚实的按照正确的方式生成了账户,即
- 私钥 s k U sk_U skU与用户公钥 p k U pk_U pkU相关联。
- 账户中的使用的 a a a就是前面秘密分享出来的 a a a,且可以通过打开承诺 c o m M com_{\mathbb{M}} comM进行还原。
- 初始化账户各项值为0。
- 用户知道生成账户 a c c B acc^{\mathfrak{B}} accB和承诺 c o m M com_{\mathbb{M}} comM的两个随机数。
- 还需要证明 x x x从1开始,且每一次交易递增1。
- 发送注册信息:用户广播自己的 c o m M com_{\mathbb{M}} comM,然后通过P2P安全通道向维护者们分别发送注册信息
每个维护人员 M j M_j Mj
- 注册验证:此时每一个维护人员将会分别从广播信道和P2P通道收到的消息里,找到同一个用户
U
U
U,对其进行验证,如果满足
- 账户已存在
- 公钥不匹配
- 零知识证明不通过
- 承诺不通过
- 未通过KYC(Know your customer)的验证
则忽略掉注册请求,否则就为其生成一条用户记录 U R = ( a j , r j , c o m M , U ) UR=(a_j,r_j,com{\mathbb{M},U}) UR=(aj,rj,comM,U)存在自己的账本里,接着为该账户生成盲签名 σ j B \sigma^{\mathfrak{B}}_j σjB然后,P2P发送给用户。
- 账户绑定:用户收到所有的盲签名后,进行解盲然后聚合为新的签名 σ B \sigma^{\mathfrak{B}} σB和自己的账户绑定。
再收到用户已接受的信息后,央行也会将交易信息
T
l
B
=
ψ
\mathsf{Tl}_B = \psi
TlB=ψ发送给维护者
货币发行
即央行给用户发行资金。
用户:
- 用户向央行提出申请,央行会通过安全匿名信道发送 v v v价值的金额,如果此时用户在Idle状态,则会通过安全匿名通道向央行发送一个新随机数 ρ \rho ρ,该随机数与阈值ElGamal加密生成的 ψ \psi ψ有关。
- 用户收到继续的指令之后,将交易信息
T
l
U
=
{
ψ
,
a
c
c
n
e
w
,
B
,
σ
M
R
n
d
,
T
,
v
,
π
}
\mathsf{Tl}_U=\{\psi,acc^{new,\mathfrak{B}},\sigma^{Rnd}_{\mathbb{M}},T,v,\pi\}
TlU={ψ,accnew,B,σMRnd,T,v,π}发送给维护者,交易信息计算过程大致如下
- 对用户公钥和交易价值进行加密:使用随机数 ρ \rho ρ、公钥 p k U pk_U pkU和 g v g^v gv计算出加密公钥和交易简直密文的 ψ = ( ψ 1 , ψ 2 , ψ 3 ) = ( g ρ , p k 1 , M ρ ⋅ p k U , p k 2 , M ρ ⋅ g v ) \psi=(\psi_1,\psi_2,\psi_3)=(g^\rho,\mathsf{pk}_{1,M}^\rho\cdot\mathsf{pk}_{\mathsf{U}},\mathsf{pk}_{2,M}^\rho\cdot g^v) ψ=(ψ1,ψ2,ψ3)=(gρ,pk1,Mρ⋅pkU,pk2,Mρ⋅gv)。
- 更新账户和签名:计算出新账户 a c c n e w , B acc^{new,\mathfrak{B}} accnew,B,账户的更新算法为
a
c
c
n
e
w
=
(
B
n
e
w
,
S
n
e
w
,
R
n
e
w
,
s
k
U
,
a
x
+
1
,
a
)
=
(
B
o
l
d
+
v
,
S
o
l
d
,
R
o
l
d
+
v
,
s
k
U
,
a
x
⋅
a
,
a
)
acc^{new}={(B^{new},S^{new},R^{new},sk_U,a^{x+1},a)} = (B^{old}+v,S^{old},R^{old}+v,sk_U,a^x \cdot a ,a)
accnew=(Bnew,Snew,Rnew,skU,ax+1,a)=(Bold+v,Sold,Rold+v,skU,ax⋅a,a)
,然后计算新的签名
σ
M
R
n
d
\sigma^{Rnd}_{\mathbb{M}}
σMRnd(这个和注册协议里的获取方式一样,通过TBS门限盲签名计算)。
- 更新交易标签:计算交易标签 T = g a x + 1 T=g^{a^{x+1}} T=gax+1,该标签每次交易都会递增,可以迫使用户每次都是用最新的账户。
- 零知识证明:最后再次进行零知识证明,证明自己是诚实的进行协议的,即。
- 新账户中的私钥与用在 ψ \psi ψ中的公钥是对应的。
- T T T的生成也是正确的,它的指数是使用新账户的第5个参数生成的。
- σ M R n d \sigma^{Rnd}_{\mathbb{M}} σMRnd是 σ M \sigma_{\mathbb{M}} σM的重随机化且 σ M \sigma_{\mathbb{M}} σM是聚合了 α \alpha α个不同的有效维护者的在原账户上的签名的签名。
- 新账户是在旧帐户和在 ψ \psi ψ中的 v v v的基础上更新的。
- 用户知道随机数 r r e g r_{reg} rreg,该随机数用于生成新账户、新签名和门限签名。
- 使用安全发送给交易信息给维护者,收到上一个维护者的确认信息再发给下一个。
央行 B B B:
- 在确认用户已收到交易后,央行也会发送交易信息 T l B = ψ \mathsf{Tl}_B = \psi TlB=ψ给维护者,收到上一个维护者的确认信息再发给下一个。
每个维护人员 M j M_j Mj:
- 交易验证:接收用户交易信息解析验证,若交易标识符已经存在于交易账本里(包含发行、支付交易、交易终止),或者零知识证明验证、签名验证不通过则忽略掉此交易信息。
- 账本交易双方记录:先记录该交易到账本里,等收到同样经过验证的央行交易信息 T l B \mathsf{Tl}_B TlB时(对比消息中的签名 ψ = ψ ′ \psi = \psi' ψ=ψ′),将交易双方拼为交易对 ( T l B , T l U ) (\mathsf{Tl}_B,\mathsf{Tl}_U) (TlB,TlU)然后存在账本里。
- 账本交易id:在账本中存下交易标识 t i d = ( ψ , T ) t_{id} = (\psi,T) tid=(ψ,T),生成新的盲签名 σ j n e w , B \sigma_j^{new,\mathfrak{B}} σjnew,B然后发送给用户
用户:
- 在收到盲签名后,进行解盲然后聚合出新的盲签名 σ M n e w \sigma_{\mathbb{M}}^{new} σMnew。
支付
即正常的交易。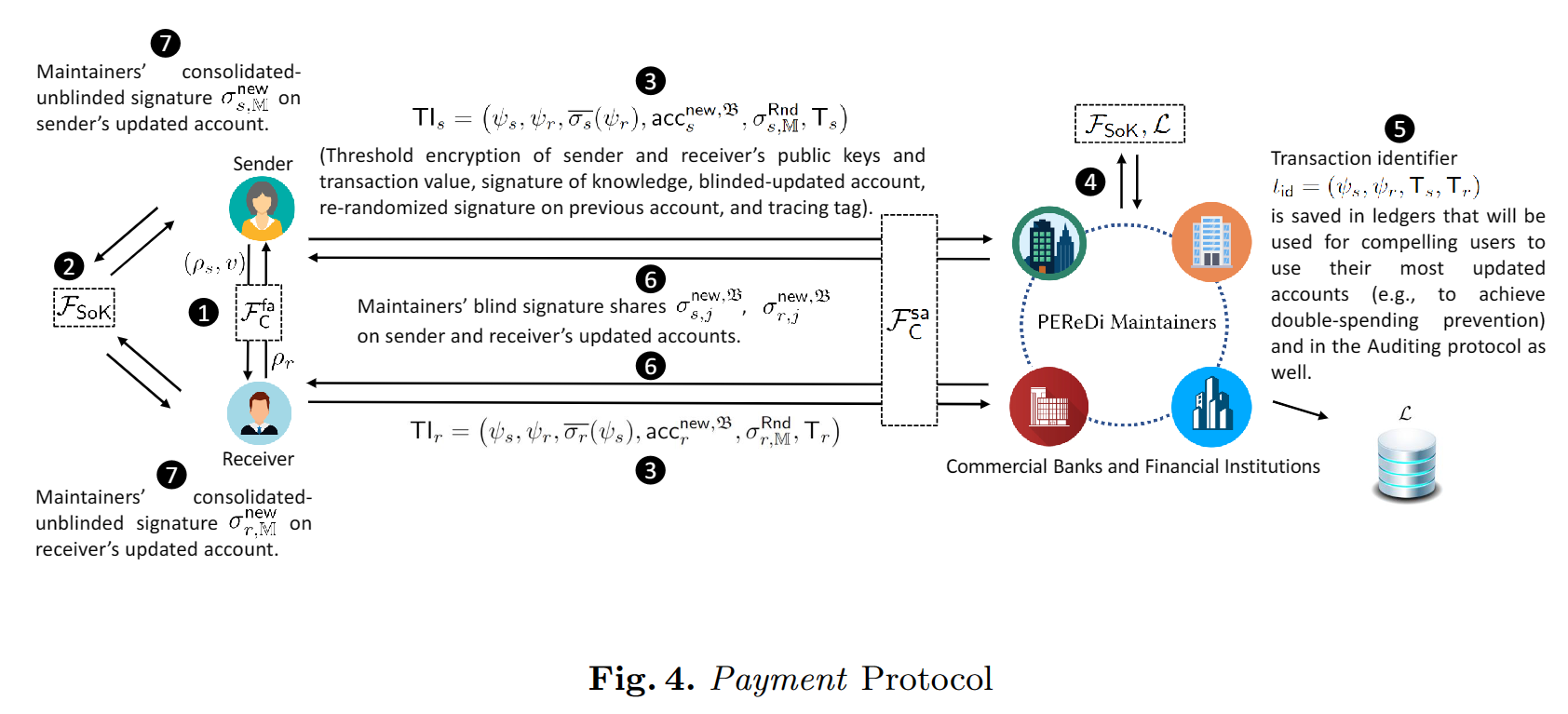
支付用户 U s U_s Us
- 如果处于 Idle,则将初始化支付协议,通过完全匿名信道向接收用户 U r U_r Ur发送交易价值 v v v和与阈值签名 ψ s \psi_s ψs生成有关的随机数 ρ s \rho_s ρs这个签名生成和前面 ψ \psi ψ类似,都是对用户公钥 p k s pk_s pks和交易价值 v v v的加密。
接收用户 U r U_r Ur
- 收到后,通过完全匿名信道返回类似的随机数 ρ r \rho_r ρr(与 ψ r \psi_r ψr)有关。,该签名则是用户公钥 p k r pk_r pkr的加密
接收用户和支付用户
-
U
s
U_s
Us和
U
r
U_r
Ur计算交易信息
T
l
s
\mathsf{Tl}_s
Tls和
T
l
r
\mathsf{Tl}_r
Tlr。其中
T
l
s
=
(
ψ
s
,
ψ
r
,
σ
s
‾
(
ψ
r
)
,
a
c
c
s
n
e
w
,
B
,
σ
s
,
M
R
n
d
,
T
s
)
\mathsf{Tl}_s=(\psi_s,\psi_r,\overline{\sigma_s}(\psi_r),\mathsf{acc}_s^{\mathsf{new},\mathfrak{B}},\sigma_{s,\mathbb{M}}^{\mathsf{Rnd}},\mathsf{T}_s)
Tls=(ψs,ψr,σs(ψr),accsnew,B,σs,MRnd,Ts),计算过程如下
- 计算门限加密,加密公钥和交易价值 ψ s = ( ψ s , 1 , ψ s , 2 , ψ s , 3 ) = ( g ρ s , p k 1 , M ρ s ⋅ p k s , p k 2 , M ρ s ⋅ g v ) \psi_s=(\psi_{s,1},\psi_{s,2},\psi_{s,3})=(g^{\rho_s},\mathsf{pk}_{1,\mathbb{M}}^{\rho_s}\cdot\mathsf{pk}_{s},\mathsf{pk}_{2,\mathbb{M}}^{\rho_s}\cdot g^v) ψs=(ψs,1,ψs,2,ψs,3)=(gρs,pk1,Mρs⋅pks,pk2,Mρs⋅gv)和 ψ r = ( ψ r , 1 , ψ r , 2 ) = ( g ρ r , p k 1 , M ρ r ⋅ p k r ) \psi_r=(\psi_{r,1},\psi_{r,2})=(g^{\rho_r},\mathsf{pk}_{1,\mathbb{M}}^{\rho_r}\cdot\mathsf{pk}_r) ψr=(ψr,1,ψr,2)=(gρr,pk1,Mρr⋅pkr), σ s ‾ ( ψ r ) \overline{\sigma_s}(\psi_r) σs(ψr)是对 ψ r \psi_r ψr的知识签名。
- 更新账户和签名:方法和货币发行类似 a c c s n e w = ( B s n e w , S s n e w , R s n e w , s k s , a s x s + 1 , a s ) = ( B s o l d + v , S s o l d , R s o l d + v , s k s , a s x ⋅ a s , a s ) acc^{new}_s={(B^{new}_s,S^{new}_s,R^{new}_s,sk_s,a_s^{x_s+1},a_s)} = (B^{old}_s+v,S^{old}_s,R^{old}_s+v,sk_s,a^x_s \cdot a_s ,a_s) accsnew=(Bsnew,Ssnew,Rsnew,sks,asxs+1,as)=(Bsold+v,Ssold,Rsold+v,sks,asx⋅as,as)
- 更新交易标签:计算交易标签 T s = g a x + 1 T_s=g^{a^{x+1}} Ts=gax+1,该标签每次交易都会递增,可以迫使用户每次都是用最新的账户。
- 零知识证明:证明自己诚实进行协议,即
- 新账户中的私钥与用在 ψ s \psi_s ψs中的公钥是对应的。
- T s T_s Ts的生成也是正确的,它的指数是使用新账户的第5个参数生成的。
- σ s , M R n d \sigma^{Rnd}_{s,\mathbb{M}} σs,MRnd是 σ s , M \sigma_{s,\mathbb{M}} σs,M的重随机化且 σ s , M \sigma_{s,\mathbb{M}} σs,M是聚合了 α \alpha α个不同的有效维护者的在原账户上的签名的签名。
- 新账户是在旧帐户和在 ψ s \psi_s ψs中的 v v v的基础上更新的。
- 用户知道随机数 r s r_s rs,该随机数用于生成新账户、新签名和门限签名。
T I r = ( ψ s , ψ r , σ r ‾ ( ψ s ) , a c c r n e w , B , σ r , M R n d , T r ) \mathsf{TI}_r=(\psi_s,\psi_r,\overline{\sigma_r}(\psi_s),\mathsf{acc}_r^{\mathsf{new},\mathfrak{B}},\sigma_{r,\mathbb{M}}^{\mathsf{Rnd}},\mathsf{T}_r) TIr=(ψs,ψr,σr(ψs),accrnew,B,σr,MRnd,Tr)的计算过程类似。
- 双方将交易信息发送给每一个维护人员,收到上一个维护者的确认信息再发给下一个。
每个维护人员 M j M_j Mj
- 交易验证:接收用户交易信息解析验证,若交易标识符已经存在于交易账本里(包含发行、支付交易、交易终止),或者零知识证明验证、签名验证不通过则忽略掉此交易信息。
- 账本交易双方记录:先记录该交易到账本里,等收到同样经过验证的另一方交易信息后时(对比消息中的签名 ( ψ s , ψ r ) = ( ψ s ′ , ψ r ′ ) (\psi_s,\psi_r) = (\psi_s',\psi_r') (ψs,ψr)=(ψs′,ψr′)),将交易双方拼为交易对 ( T l s , T l r ) (\mathsf{Tl}_s,\mathsf{Tl}_r) (Tls,Tlr)然后存在账本里。
- 账本交易id:在账本中存下交易标识 t i d = ( ψ , T ) t_{id} = (\psi,T) tid=(ψ,T),为双方生成新的盲签名 σ s , j n e w , B , σ r , j n e w , B \sigma_{s,j}^{new,\mathfrak{B}},\sigma_{r,j}^{new,\mathfrak{B}} σs,jnew,B,σr,jnew,B然后发送给对应用户。
接收用户和支付用户
- 收到消息后解盲然后聚合签名。
交易中止
特殊情况,即维护者收到了一方的交易信息并通过验证,但未收到交易另一方的有效交易信息,不能满足交易对,也就表示用户无法为自己新账户的生成收到足够数量的盲签名。此时
支付用户
- 发送交易中止信息 A R = ( a c c r , B , σ M R n d , T , π ) \mathrm{AR~=~(acc^{r,\mathfrak{B}},\sigma_{M}^{Rnd},T,\pi)} AR = (accr,B,σMRnd,T,π)给维护者,其中
- 更新账户为 a c c r = ( B r , S r , R r , s k U , a x + 1 , a ) = ( B o l d , S o l d , R o l d , s k U , a x ⋅ a , a ) acc^r={(B^r,S^r,R^r,sk_U,a^{x+1},a)} = (B^{old},S^{old},R^{old},sk_U,a^x \cdot a ,a) accr=(Br,Sr,Rr,skU,ax+1,a)=(Bold,Sold,Rold,skU,ax⋅a,a), a c c r , B acc^{r,\mathfrak{B}} accr,B代表盲化版本。
- T = g a x + 1 T = g^{a^{x+1}} T=gax+1为最近使用的交易tag
- π \pi π为相应的零知识证明
交易信息的计算过程如下
- 计算 a c c r , B , σ M R n d acc^{r,\mathfrak{B}},\sigma_{M}^{Rnd} accr,B,σMRnd
- 执行零知识证明,即
- T T T的生成也是正确的,它的指数是使用新账户的第5个参数生成的。
- σ M R n d \sigma^{Rnd}_{\mathbb{M}} σMRnd是 σ M \sigma_{\mathbb{M}} σM的重随机化且 σ s , M \sigma_{s,\mathbb{M}} σs,M是聚合了 α \alpha α个不同的有效维护者的在原账户上的签名的签名。
- 新账户是在旧帐户的基础上更新的,也就是金额回到交易之前的状态。
- 用户知道随机数 r a b r r_{abr} rabr,该随机数用于生成新账户、新签名和门限签名。
- 发送交易中止信息 A R = ( a c c r , B , σ M R n d , T , π ) \mathrm{AR~=~(acc^{r,\mathfrak{B}},\sigma_{M}^{Rnd},T,\pi)} AR = (accr,B,σMRnd,T,π)给每一个维护人员,收到上一个维护者的确认信息再发给下一个。
每个维护人员 M j M_j Mj
- 交易验证:解析消息,若交易标识符已经被中止(账本里存在一条中止记录),或者零知识证明验证、签名验证不通过则忽略掉此交易信息。
- 拜占庭投票:若自己的账本里存在当前交易的标签 T T T(发行或者支付交易),则向拜占庭协议里输入1,否则输入0。
- 若拜占庭结果为1,代表至少有一个诚实的维护人员存下了此前的交易,则
- 存下了交易的诚实维护人员将该交易对 ( T l s , T l r ) (\mathsf{Tl}_s,\mathsf{Tl}_r) (Tls,Tlr)通过认证信道发送给其他的维护人员。
- 收到的信息的维护人员对该交易对进行验证,无效则忽略,有效则对该交易对 a c c s n e w , B , a c c r n e w , B \mathsf{acc}_s^{\mathsf{new},\mathfrak{B}},\mathsf{acc}_r^{\mathsf{new},\mathfrak{B}} accsnew,B,accrnew,B进行签名 σ s , j n e w , B , σ r , j n e w , B \sigma_{s,j}^{new,\mathfrak{B}},\sigma_{r,j}^{new,\mathfrak{B}} σs,jnew,B,σr,jnew,B。
- 如果没有存下相关交易对和交易标签,则存下,然后将对应签名发送给对应交易双方。
接收用户和支付用户收到消息后解盲然后聚合签名,交易完成,同时代表中止交易失败。
- 若拜占庭结果为0,代表大部分维护者的账本是没有该交易标签的。
- 已经存有交易对的维护者,从自己的账本里删除掉该交易对信息。
- 存储下新的交易中止信息的标签 t i d = ( A b o r t e d , T ) t_{id} = (Aborted,T) tid=(Aborted,T)。
- 对重新刷新的账户进行签名 σ j r , B \sigma_{j}^{r,\mathfrak{B}} σjr,B,然后发送给用户。
接收用户收到消息后解盲然后聚合签名,交易完成,中止交易成功。
审计
隐私撤销
提交完全匿名的交易对, 审计委员会撤销其隐私并返回交易的元数据,即双方用户以及交易价值。
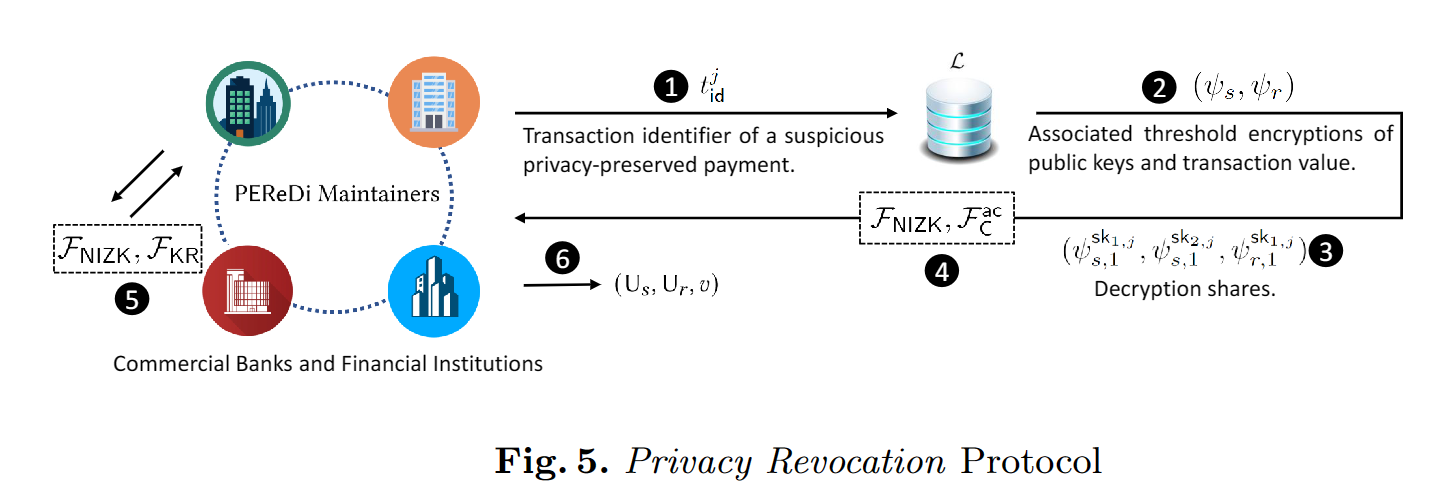
收到撤销特定交易tag的指令之后,
每个维护人员
- 从账本里查找到与该tag t i d t_{id} tid相关的加密交易对 ( ψ s , ψ r ) (\psi_s,\psi_r) (ψs,ψr),并对其解密得到 ( ψ s , 1 s k 1 , j , ψ s , 1 s k 2 , j , ψ r , 1 s k 1 , j ) (\psi_{s,1}^{sk_1,j},\psi_{s,1}^{sk_2,j},\psi_{r,1}^{sk_1,j}) (ψs,1sk1,j,ψs,1sk2,j,ψr,1sk1,j),接着调用零知识证明协议,证明解密正确。
- 通过认证信道接收来自其他维护人员的信息(需要达到门限阈值的数量)和相应拉格朗日系数,调用恢复函数恢复出交易信息里的双方用户公钥 ( p k s , p k r ) (pk_s,pk_r) (pks,pkr)以及交易值 g v g^v gv。同样需要调用零知识证明协议证明解密正确。
- 调用密钥检索函数,通过公钥寻找到对应用户,并通过
g
v
g^v
gv计算出
v
v
v。
追踪溯源
提交用户的标识符,审计委员会追溯出该用户的所有交易。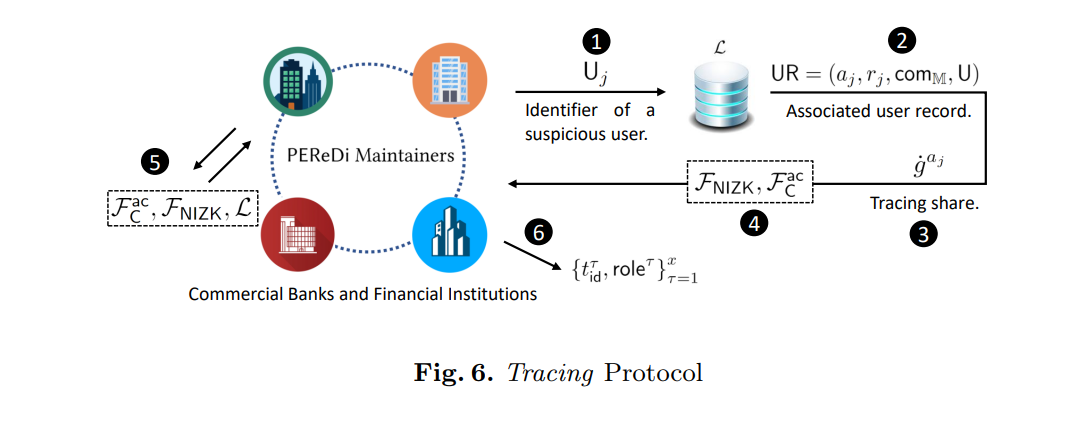
通过用户标识符,从注册协议中查到用户的交易计数器
a
a
a的秘密分享,
维护者相互计算交易标签,直到该标签不存在于账本上,由此找到用户最近的交易。
收到追溯的指令之后,
每个维护人员
- 从账本找到用户注册记录,使用零知识证明,证明里面的 a j a_j aj是之前得到的那个,可以通过注册协议广播的 c o m j ~ \tilde{\mathsf{com}_j} comj~得证,即证明 c o m j ~ ∈ c o m M \tilde{\mathsf{com}_j} \in com_{\mathbb{M}} comj~∈comM。
- 通过认证信道接收其他维护人员的信息 x ‾ j = ( соm ~ j , g ˙ a j , g ˙ ) \overline{\mathrm{x}}_j=(\tilde{\text{соm}}_j,\dot{g}^{a_j},\dot{g}) xj=(соm~j,g˙aj,g˙)以及对应的零知识证明proof(需要达到门限阈值的数量)和相应拉格朗日系数,其中 g ˙ = g a e , e ← 0 \dot{g}=g^{a^e},e\leftarrow 0 g˙=gae,e←0,证proof并计算出 g ˙ a \dot{g}^{a} g˙a
- 接着从自己账本里寻找包含此交易tag= g ˙ a \dot{g}^{a} g˙a的交易,若存在,则将交易标签往前提一个 e ← e + 1 e\leftarrow e+1 e←e+1,并存该交易相关 t i d t_{id} tid和相应参与双方信息。若不存在,则向其他所有参与者发送消息说明自己这里没有包含此交易tag= g ˙ a \dot{g}^{a} g˙a的交易。
- 若收到达到门限阈值数量个不包含交易tag的消息,则可以输出目前位置记录的所有交易信息(
t
i
d
t_{id}
tid,相应参与双方信息)。
小结
- 交易中止这块是特殊情况,不是很理想。账户丢失被盗这类问题没有解决。
- 离线情景没有考虑
参考
Kiayias, Aggelos, Markulf Kohlweiss, and Amirreza Sarencheh. “Peredi: Privacy-enhanced, regulated and distributed central bank digital currencies.” Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security. 2022.