Day21｜二叉树part07：530.二叉搜索树的最小绝对差、501.二叉搜索树中的众数、236. 二叉树的最近公共祖先

news2024/9/23 7:28:23

530. *二叉搜索树的最小绝对差（双指针题型）

众所周知二叉搜索树的中序遍历序列是一个有序数组，因此最基本的方法就是遍历得到中序序列再进行计算，实际上可以用双指针法，记录中序遍历前一个指针和当前指针的差值：

class Solution {
    private int res = Integer.MAX_VALUE;
    private TreeNode pre = null;

    private void traversal(TreeNode cur){
        if(cur == null){
            return;
        }
        traversal(cur.left);
        if(pre != null){
            res = Math.min(res, Math.abs(cur.val - pre.val));
        }
        pre = cur;
        traversal(cur.right);
    }
    public int getMinimumDifference(TreeNode root) {
        traversal(root);
        return res;
    }
}

501.二叉搜索树中的众数

这里分两种方法，一种是当作普通的二叉树来做，一种是利用BST的性质来做。

使用普通的二叉树，遍历一遍，将频率用Map存储，然后找到频率最高的。

class Solution {
        private Map<Integer, Integer> times = new HashMap<>();

        void traversal(TreeNode node) {
            if (node == null) {
                return;
            }
            traversal(node.left);
            times.put(node.val, times.getOrDefault(node.val, 0) + 1);
            traversal(node.right);
        }

        public int[] findMode(TreeNode root) {
            //1. 得到（值，频率）的map
            traversal(root);
            int maxCount = 0;
            for(Integer count: times.values()){
                maxCount = Math.max(maxCount, count);
            }
            
            //2. 将频率最高的key找到
            List<Integer> res = new ArrayList<>();
            for (Map.Entry<Integer, Integer> entry : times.entrySet()) {
                if (entry.getValue() == maxCount) {
                    res.add(entry.getKey());
                }
            }
            
            //3. 根据key去找value并转化成数组
            int[] result = new int[res.size()];
            for (int i = 0; i < res.size(); i++) {
                result[i] = res.get(i);
            }
            return result;
        }
    }

java的数组真的太麻烦了，又是Map转List再转数组的，不要乱；

利用BST性质的解法：

class Solution {
        public void test(){
            TreeNode root = new TreeNode(0);
//            root.right = new TreeNode(2);
//            root.right.left = new TreeNode(2);
            findMode(root);
        }
        private List<Integer> res = new ArrayList<>();
        private int count = 0;

        private int maxCount = 0;
        private TreeNode pre = null;

        void traversal(TreeNode node) {
            if(node == null){
                return;
            }
            traversal(node.left);
            if(pre == null){
                count = 1;
            }else if(node.val == pre.val){
                count++;
            }else{
                count = 1;
            }
            pre = node;
            if(count == maxCount){
                res.add(node.val);
            }
            if(count > maxCount){
                maxCount = count;
                res.clear();
                res.add(node.val);
            }

            traversal(node.right);
        }

        public int[] findMode(TreeNode root) {
            traversal(root);
            int[] array = res.stream().mapToInt(i->i).toArray();
            return array;
        }
    }

也是需要两个指针一个pre一个cur，这样只遍历一次二叉树就可以获取众数节点。

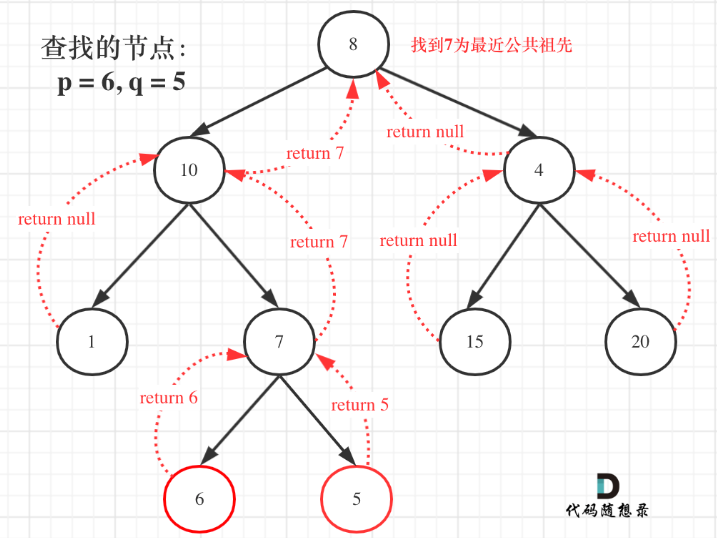
236. ***二叉树的最近公共祖先（LCA）

公共祖先的定义：

“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

（这里是求最近公共祖先。因为root是所有节点的公共祖先 )

需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从底向上的遍历方式。
解法思路：如果一个节点能够在它的左右子树中分别找到 p 和 q，则该节点为 LCA 节点。这样可以借助find函数得到本题的解法：
判断逻辑是如果递归遍历遇到q，就将q返回，遇到p 就将p返回，那么如果左右子树的返回值都不为空，说明此时的中节点，一定是q 和p 的最近祖先。

class Solution {
    private TreeNode find(TreeNode node, TreeNode p, TreeNode q){
        if(node == null || node == p || node == q){
            return node;
        }
        TreeNode left = find(node.left, p ,q);
        TreeNode right = find(node.right, p , q);
       if(left != null && right != null){
           return node;
       }else if(left != null && right == null){
           return left;
       }else if(left == null && right != null){
           return right;
       }else{
           return null;
       }
    }
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

        return find(root, p ,q);
    }
}