【ZZULI数据结构实验一】多项式的四则运算
- ♋ 结构设计
- ♋ 方法声明
- ♋ 方法实现
- 🐇 定义一个多项式类型并初始化---CreateDataList
- 🐇 增加节点---Getnewnode
- 🐇 打印多项式类型的数据-- PrintPoly
- 🐇 单链表的尾插--Listpush_back
- 🐇 多项式相加--PolyAdd
- 🐇 多项式相减-- PolySub
- 🐇 多项式相乘--PolyMult
- 🐇 销毁单链表--Destroy
- ♋ 测试
- 优化

📃博客主页: 小镇敲码人
🚀 欢迎关注:👍点赞 👂🏽留言 😍收藏
🌏 任尔江湖满血骨,我自踏雪寻梅香。 万千浮云遮碧月,独傲天下百坚强。 男儿应有龙腾志,盖世一意转洪荒。 莫使此生无痕度,终归人间一捧黄。🍎🍎🍎
❤️ 什么?你问我答案,少年你看,下一个十年又来了 💞 💞 💞
前言:本篇博客旨在个人学习,实现了多项式的加减乘运算,对代码的正确性不作100%的保证。
♋ 结构设计
这里我们使用带头单链表来存储多项式的数据(各项系数及其幂次),也可以用顺序表来存数据,但是这样头插不太方便,而且需要另外创建一个节点类型放一个项的系数和幂次。如果你对单链表还留有疑问,可以看看博主的这篇文章单链表详解
这个和下面的方法声明都放到头文件里。
typedef struct DataList
{
int coe;//系数
int power;//幂次
struct DataList* next;
}List;
♋ 方法声明
List* CreateDataList();//输入数据并构造数据单链表的函数
List* PolyAdd(List* A,List* B);//实现多项式相加
List* PolySub(List* A,List* B);//实现多项式相减
List* PolyMult(List* A,List* B);//实现多项式相乘
List* Getnewnode(int coe_, int power_);//申请一个节点,并初始化
void PrintPoly(List* A);//打印多项式
void Listpush_back(List* C, int coe_,int power_);//尾插节点
void Destroy(List* A);//销毁节点
♋ 方法实现
方法实现放到.c文件里。
🐇 定义一个多项式类型并初始化—CreateDataList
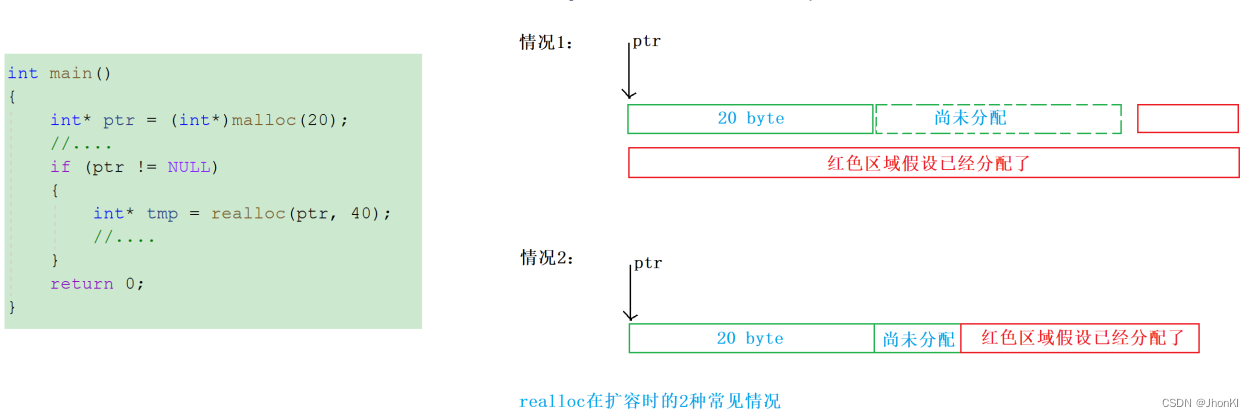
初始化就是放数据的过程,这里直接走一个循环,然后申请空间就可以了,如果你对申请空间有疑问,请看博主这篇文章C语言动态内存管理,这里我们规定输入数据时,应该先输入幂次大的节点(先输入系数,再输入幂次),然后下一次节点链接我们直接头插就可以保证多项式类型的节点从左到右是按照幂次升序存储的(方便后序的四则运算),单链表的头插比尾插简单(尾插需要找尾)。
这里当然你也可以乱输入,增加一个排序函数就可以(按照幂次排)。小小实验我们并不需要这么麻烦,直接输入让它有序就可以了(dog。
这里我们选择带头的单链表,是为了避免头插时没有数据的判空。
代码实现:
List* CreateDataList()
{
int coe_ = 0, power_ = 0;//初始化两个临时变量,用于输入每个节点的数据
printf("请依次按照幂次从大到小输入数据,先输入多项式的系数,后输入幂次:\n");//提示信息
List* Head = Getnewnode(-1, -1);//设置空的头节点
while(scanf("%d%d", &coe_, &power_) != EOF)
{
List* newnode = Getnewnode(coe_, power_);
newnode->next = Head->next;
Head->next = newnode;
printf("请依次按照幂次从大到小输入数据,先输入多项式的系数,后输入幂次:\n");//提示信息,每次输入数据前都打印一次,这里会多打印一次无伤大雅
}
return Head;//返回头节点
}
🐇 增加节点—Getnewnode
我们在很多地方都需要申请节点,而且要初始化,为了不造成代码冗余,我们把其单独作为一个函数写出来,用的时候直接调用就好了。
代码实现:
List* Getnewnode(int coe_, int power_)
{
List* newnode = (List*)malloc(sizeof(List));//在堆上申请空间
if (newnode == NULL)//如果申请失败
{
printf("malloc Failed\n");
exit(-1);
}
//初始化新节点
newnode->coe = coe_;
newnode->power = power_;
newnode->next = NULL;//注意next要置空,否则会造成野指针的问题
return newnode;//返回新节点
}
🐇 打印多项式类型的数据-- PrintPoly
这个函数就是单纯的打印,为了方便我们后序打印多项式类型看相加和相乘、以及相减的结果,当然你也可以通过调试查看。
代码实现:
void PrintPoly(List* A)//打印多项式
{
assert(A);//防止A为空,我们不能对空解引用,assert函数相当于暴力检查
List* cur = A->next;//从头节点的下一个节点开始遍历,因为头节点不存数据
if (cur == NULL)//cur为空
printf("多项式为空\n");
while (cur != NULL)//cur不为空
{
if (cur->coe > 0 && cur != A->next)
printf("+%d*(x^%d)", cur->coe, cur->power);
else
printf("%d*(x^%d)", cur->coe, cur->power);
cur = cur->next;
}
printf("\n");
}
🐇 单链表的尾插–Listpush_back
在多项式相加的函数里面我们会用到单链表的尾插,如果你对其原理不太熟悉,请自行翻阅博主之前的博客。
代码实现:
void Listpush_back(List* C, int coe_, int power_)//尾插数据
{
assert(C);//C不为空
List* newnode = Getnewnode(coe_, power_);//申请新节点并初始化
List* tail = C;
while (tail->next)//找尾节点
{
tail = tail->next;
}
tail->next = newnode;//把新节点链接到尾节点的后面
}
🐇 多项式相加–PolyAdd
我们的多项式相加的思路类似双指针,O(N)时间复杂度内完成。
下面我们画图来分析一下这个过程:
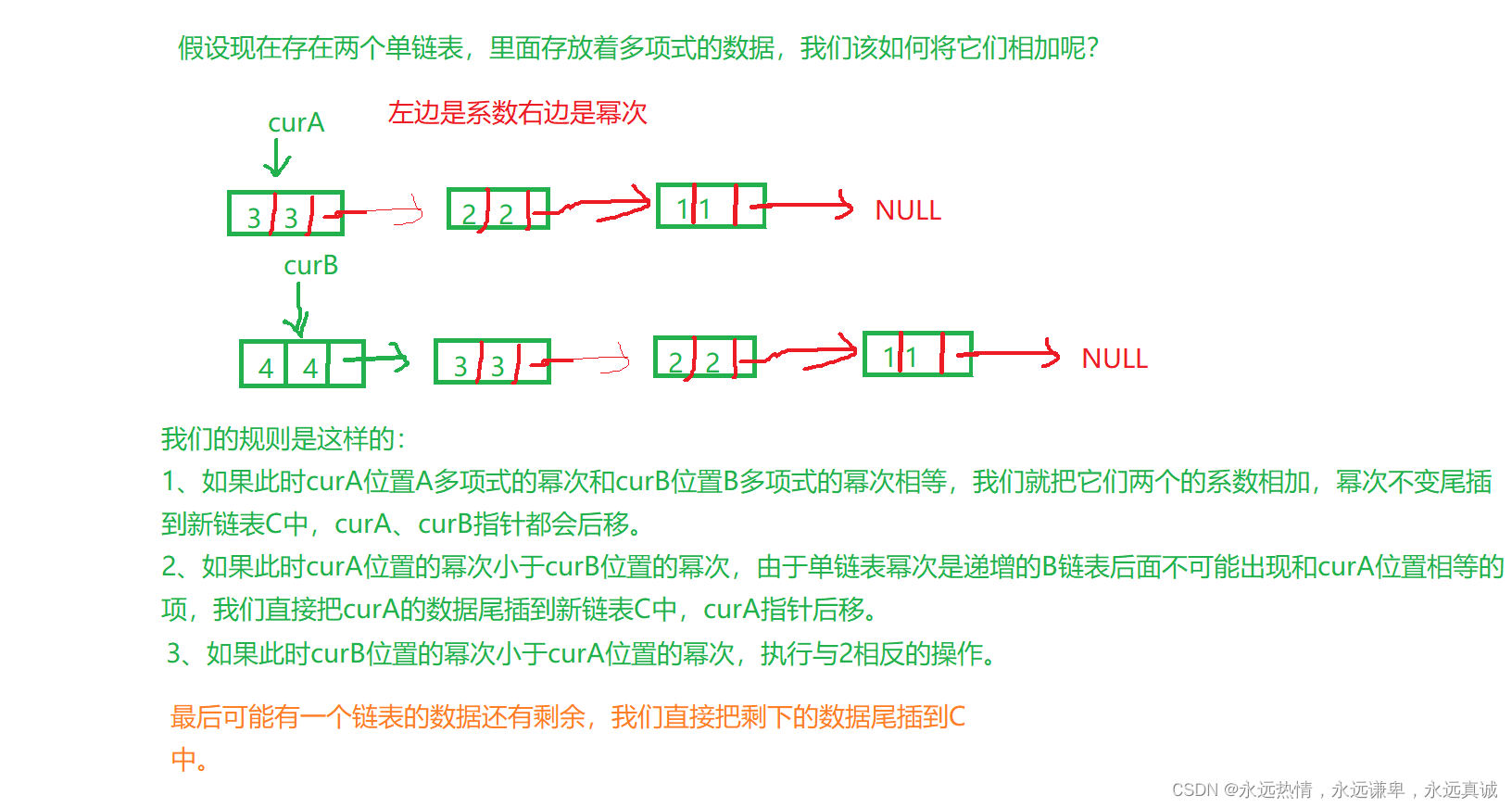
- 注意:这里为什么是尾插到C中呢?
因为尾插才能保证C中数据是按幂次升序的,因为A和B中的数据都是按幂次升序排列的,我们为什么不把数据放到A和B中的其中一个呢,因为这样会改变A和B的内容,后面我们可能会对A、B做其它操作。
代码实现:
List* PolyAdd(List* A, List* B)
{
assert(A && B);//断言,防止A或者B为空指针
List* C = Getnewnode(-1, -1);//创建新的链表C,我们不希望改变链表A和B的值,所以把它们相加的结果存入C中
List* curA = A->next;
List* curB = B->next;
while (curA && curB)//A和B的当前位置都不能为空
{
if (curA->power == curB->power)//如果当前幂次相等,A和B的系数相加,幂次不变,尾插到C中
{
int new_coe = curA->coe + curB->coe;
if (new_coe != 0)
Listpush_back(C, new_coe, curA->power);
curA = curA->next;
curB = curB->next;
}
else if (curA->power < curB->power)//如果B大,尾插curA
{
Listpush_back(C, curA->coe, curA->power);
curA = curA->next;
}
else//否则尾插curB
{
Listpush_back(C, curB->coe, curB->power);
curB = curB->next;
}
}
//如果两个链表还有一个剩余,把剩下的数据尾插到C中
while (curA)
{
Listpush_back(C, curA->coe, curA->power);
curA = curA->next;
}
while (curB)
{
Listpush_back(C,curB->coe, curB->power);
curB = curB->next;
}
return C;//返回相加的结果链表的头节点指针
}
🐇 多项式相减-- PolySub
多项式相减的大致思路都和多项式相加是一样的,有一个地方要注意,因为是A-B,当B中式子多时,A中对应项的系数就是0,要给B的系数加上负号。
代码实现:
// 定义PolySub函数,接受两个多项式链表A和B作为参数,返回相减后的多项式链表C
List* PolySub(List* A, List* B)
{
// 断言A和B都不为空,确保传入的多项式链表是有效的
assert(A && B);
// 创建一个新的链表C,并初始化其头节点(这里用-1作为占位符,实际使用中可能需要其他方式初始化)
List* C = Getnewnode(-1, -1);
// 初始化两个指向A和B链表中第一个实际节点的指针curA和curB
List* curA = A->next;
List* curB = B->next;
// 当curA和curB都不为空时,循环进行以下操作
while (curA && curB)
{
// 如果curA和curB指向的项的指数相同
if (curA->power == curB->power)
{
// 计算两个相同指数项的系数之差
int new_coe = curA->coe - curB->coe;
// 如果系数之差不为0,则将新的项(系数和指数)添加到C链表中
if (new_coe != 0)
Listpush_back(C, new_coe, curA->power);
// 移动curA和curB到下一个节点
curA = curA->next;
curB = curB->next;
}
// 如果curA指向的项的指数小于curB指向的项的指数
else if (curA->power < curB->power)
{
// 将curA指向的项(系数和指数)添加到C链表中
Listpush_back(C, curA->coe, curA->power);
// 移动curA到下一个节点
curA = curA->next;
}
// 否则(即curA指向的项的指数大于curB指向的项的指数)
else
{
// 将curB指向的项的相反数(系数取反,指数不变)添加到C链表中,实现减法
Listpush_back(C, -curB->coe, curB->power);
// 移动curB到下一个节点
curB = curB->next;
}
}
// 如果curA还有剩余节点(即A的某些项在B中没有对应项)
while (curA)
{
// 将这些项(系数和指数)添加到C链表中
Listpush_back(C, curA->coe, curA->power);
// 移动curA到下一个节点
curA = curA->next;
}
// 如果curB还有剩余节点(即B的某些项在A中没有对应项)
while (curB)
{
// 将这些项的相反数(系数取反,指数不变)添加到C链表中,实现减法
Listpush_back(C, -curB->coe, curB->power);
// 移动curB到下一个节点
curB = curB->next;
}
// 返回相减后的多项式链表C
return C;
}
🐇 多项式相乘–PolyMult
相乘的思路是复用多项式相加的函数,先让B链表中的第一个项和A中各个项相乘(系数相乘,幂次相加),然后得到链表C,然后移动B继续和A中的各个相相乘,并执行多项式相加,最终得到结果。
代码实现:
// 定义PolyMult函数,接受两个多项式链表A和B作为参数,返回相乘后的多项式链表C
List* PolyMult(List* A, List* B)
{
// 断言A和B都不为空,确保传入的多项式链表是有效的
assert(A && B);
// 创建一个新的链表C,并初始化其头节点(这里用-1作为占位符)
List* C = Getnewnode(-1, -1);
// 初始化两个指针curA和curB,分别指向A和B链表中第一个实际节点
List* curA = A->next;
List* curB = B->next;
// 遍历curA指向的A链表中的每个项
while (curA)
{
// 计算当前curA指向的项与B链表中第一个项(curB指向的项)的乘积的系数和指数
int new_coe = (curA->coe) * (curB->coe);
int new_power = curA->power + curB->power;
// 将新的项(系数和指数)添加到C链表中
Listpush_back(C, new_coe, new_power);
// 移动curA到下一个节点
curA = curA->next;
}
// 初始化ans为NULL,用于存储最终的乘法结果
List* ans = NULL;
// 遍历curB指向的B链表中的每个项(从第二个项开始,因为第一个项已经在上面的循环中处理过了)
while (curB->next)
{
// 移动curB到下一个节点
curB = curB->next;
// 创建一个新的链表C1,用于存储当前curB指向的项与A链表中所有项的乘积结果
List* C1 = Getnewnode(-1, -1);
// 初始化curA,重新指向A链表中第一个实际节点
List* curA = A->next;
// 遍历curA指向的A链表中的每个项
while (curA)
{
// 计算当前curA指向的项与当前curB指向的项的乘积的系数和指数
int new_coe = (curA->coe) * (curB->coe);
int new_power = curA->power + curB->power;
// 将新的项(系数和指数)添加到C1链表中
Listpush_back(C1, new_coe, new_power);
// 移动curA到下一个节点
curA = curA->next;
}
// 将C链表和C1链表相加,得到当前curB指向的项与A链表相乘的结果,并更新ans
ans = PolyAdd(C, C1);
// 销毁C1链表,释放其占用的内存
Destroy(C1);
// 销毁C链表,释放其占用的内存(C现在保存的是上一轮的结果,我们不再需要它)
Destroy(C);
// 将ans赋值给C,准备进行下一轮的乘法运算
C = ans;
}
// 返回最终的乘法结果链表C
return C;
}
这里由于我们的C1、和C链表每一次循环都会变成新的链表,我们要及时把旧的链表空间释放,防止内存泄漏的出现。
🐇 销毁单链表–Destroy
这里在多项式相乘函数里,会出现内存泄漏,我们需要及时回收空间,防止出现这种情况。
代码实现:
void Destroy(List* A)//销毁链表
{
assert(A);
List* cur = A;
while (cur)
{
List* cur_next = cur->next;//保存下一个节点的地址
free(cur);//释放当前节点的空间
cur = cur_next;//指针指向下一个节点
}
}
♋ 测试
测试函数我们放到了main.c函数里,主要测试函数的各种功能是否和我们的预期一样,当然由于测试的数据有限,如有bug,欢迎指出。
#include"polynomial.h"
void Test()
{
List* A = CreateDataList();
List* B = CreateDataList();
List* AAddB = PolyAdd(A, B);
List* ASubB = PolySub(A, B);
List* AMultB = PolyMult(A, B);
printf("多项式A: ");
PrintPoly(A);
printf("多项式B: ");
PrintPoly(B);
printf("多项式A+B: ");
PrintPoly(AAddB);
printf("多项式A-B: ");
PrintPoly(ASubB);
printf("多项式A*B: ");
PrintPoly(AMultB);
}
int main()
{
Test();
return 0;
}
这里我们A输入:3 3 2 2 1 1
B输入: 4 4 3 3 2 2 1 1
运行结果:

和我们预期的结果一致。
这里我们A输入:1 5 1 3 1 1
B输入: 16 1 4 1 2
运行结果:
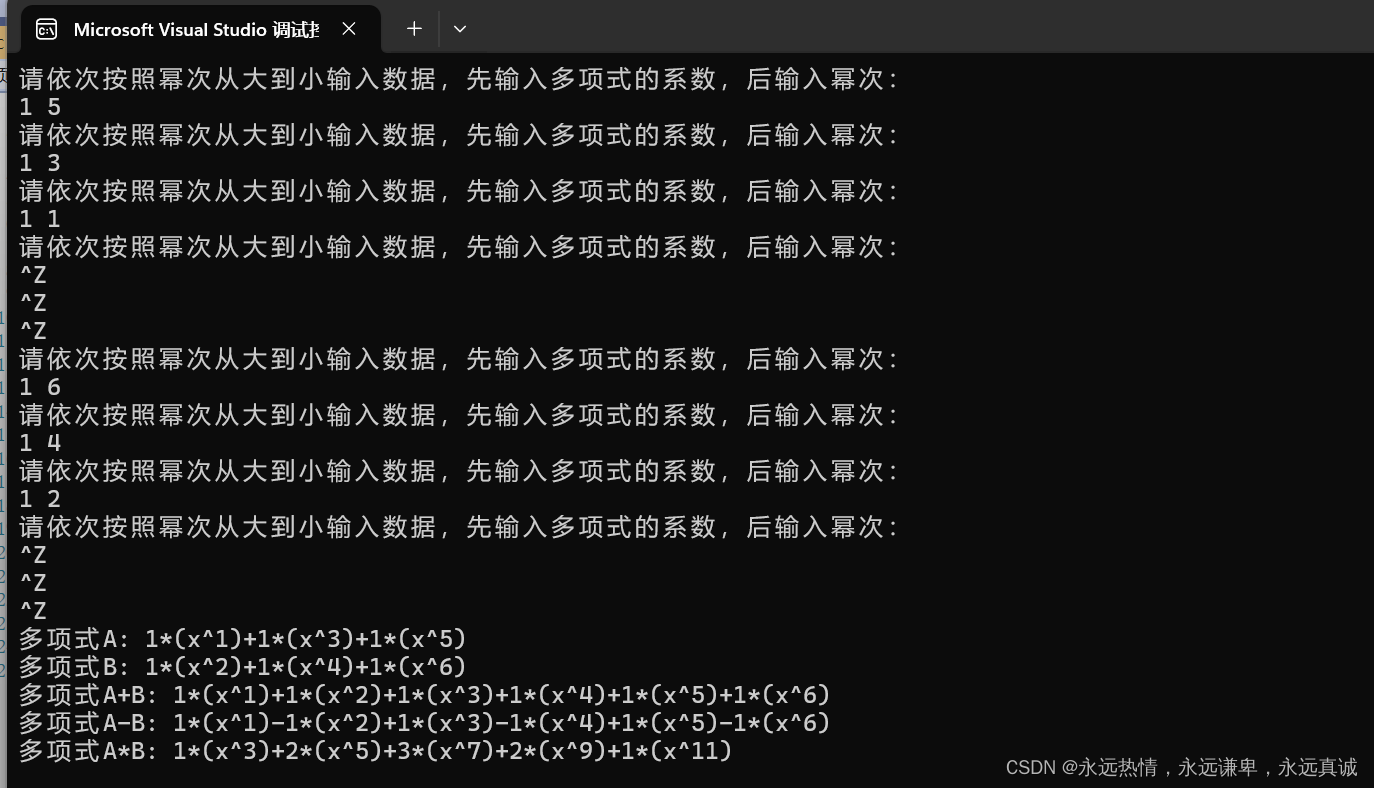
与预期结果一致。
优化
我们给我们的程序增加了一个计数排序,但是由于单链表不能下标访问,所以性能上会差一点,这里还是建议使用归并排序,因为归并排序对下标访问没有要求。
使用计数排序需要先计算单链表的长度。
// 定义一个函数,接受一个链表指针A作为参数,并返回链表的长度
int List_Length(List* A)
{
// 断言A不为空,如果A为空则程序会在这里终止,这通常用于调试时确保传入的链表是有效的
assert(A);
// 初始化一个指针cur,指向链表A的第一个实际节点(即头节点之后的节点)
List* cur = A->next;
// 初始化一个变量length,用于记录链表的长度,初始值为0
int length = 0;
// 当cur不为空时,即还有节点未遍历完时,继续循环
while (cur)
{
// 每次循环都将length加1,表示遍历到了一个节点
length++;
// 将cur移动到下一个节点,继续遍历
cur = cur->next;
}
// 返回计算得到的链表长度
return length;
}
对计数排序不太熟悉的小伙伴,可以看一下博主这篇博客。
这里我们是对有两个数据域的链表进行排序,类似对结构体进行排序,有一点不同:
代码实现:
void SortList(List* A)//按照幂次升序排序单链表,计数排序
{
CountSort(A,List_Length(A));
}
void CountSort(List* A, int n) // 链表的计数排序
{
// 初始化最大和最小值为整型最小值和最大值
int max_ = INT_MIN;
int min_ = INT_MAX;
List* cur = A->next; // 初始化cur指向链表A的第一个实际节点
// 遍历链表A,找到power的最大值和最小值
while (cur)
{
if (cur->power > max_)
max_ = cur->power;
if (cur->power < min_)
min_ = cur->power;
cur = cur->next;
}
// 计算排序范围,即最大值和最小值之间的差值加1
int range = max_ - min_ + 1;
// 分配一个整数数组,用于存储每个值的计数
int* count = (int*)malloc(sizeof(int) * range);
memset(count, 0, sizeof(int) * range); // 初始化count数组为0
// 检查内存分配是否成功
if (count == NULL)
{
printf("count malloc failed\n");
exit(-1);
}
// 再次遍历链表A,计算每个power的计数
cur = A->next;
while (cur)
{
count[cur->power - min_]++;
cur = cur->next;
}
// 创建一个新的链表C,用于存放排序后的结果
List* C = Getnewnode(-1, -1);
int length = n; // 链表A的长度
// 初始化链表C的节点,创建一个长度为n的空链表
while (length--)
{
List* newnode = Getnewnode(-1, -1);
List* next = C->next;
newnode->next = next;
C->next = newnode;
}
// 检查链表C的节点创建是否成功
if (C == NULL)
{
printf("C malloc failed\n");
exit(-1);
}
// 分配一个索引数组,用于记录每个值在排序后的链表中的起始位置
int* idx = (int*)malloc(sizeof(int) * (range + 1));
memset(idx, 0, sizeof(int) * (range + 1));
// 检查内存分配是否成功
if (idx == NULL)
{
printf("idx malloc Failed\n");
exit(-1);
}
// 计算每个值的累积计数,即该值在排序后的链表中的起始位置
for (int i = 1; i <= range; ++i)
{
idx[i] = idx[i - 1] + count[i - 1];
}
// 遍历链表A,并根据计数和索引数组将元素插入到链表C中
cur = A->next;
List* cur_ = NULL;
while (cur)
{
cur_ = C->next;
// 移动cur_到cur的power对应的插入位置
while (idx[cur->power - min_]--)
{
cur_ = cur_->next;
}
// 将cur的值复制到cur_的位置
cur_->coe = cur->coe;
cur_->power = cur->power;
// 恢复索引数组
idx[cur->power - min_]++;
cur = cur->next;
}
// 将排序后的链表C的值复制回原链表A
cur = A->next;
cur_ = C->next;
while (cur && cur_)
{
cur->coe = cur_->coe;
cur->power = cur_->power;
cur = cur->next;
cur_ = cur_->next;
}
// 销毁链表C
Destroy(C);
}
排序函数写出来后,我们在创建链表的函数后面增加一个排序调用就好了:
List* CreateDataList()
{
int coe_ = 0, power_ = 0;//初始化两个临时变量,用于输入每个节点的数据
printf("先输入多项式的系数,后输入幂次:\n");//提示信息
List* Head = Getnewnode(-1, -1);//设置空的头节点
while(scanf("%d%d", &coe_, &power_) != EOF)
{
List* newnode = Getnewnode(coe_, power_);
newnode->next = Head->next;
Head->next = newnode;
printf("先输入多项式的系数,后输入幂次:\n");//提示信息,每次输入数据前都打印一次,这里会多打印一次无伤大雅
}
SortList(Head);//按power升序排序链表
return Head;
}
运行效果:
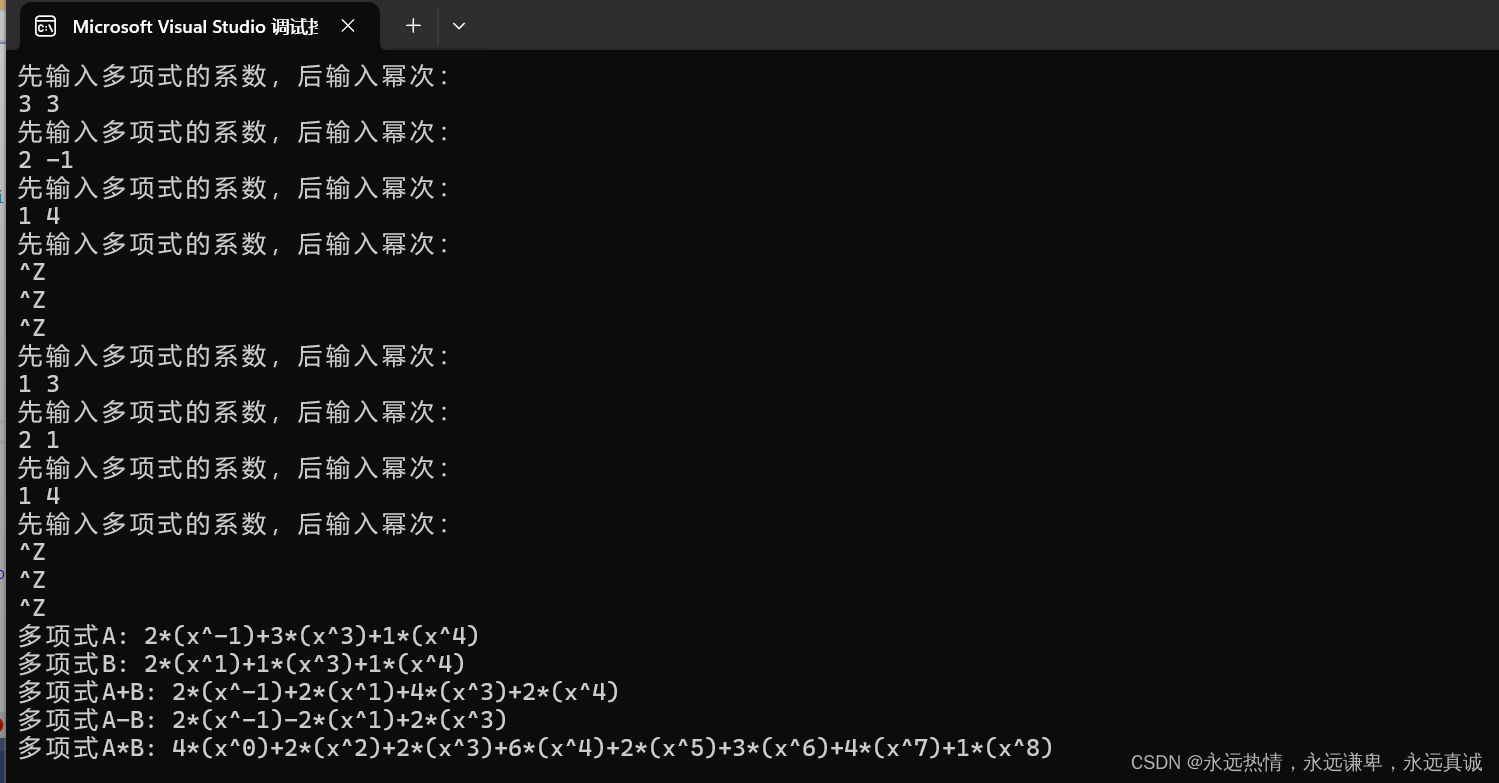
下面我们对计数排序排结构体的一些知识点做一下分析: