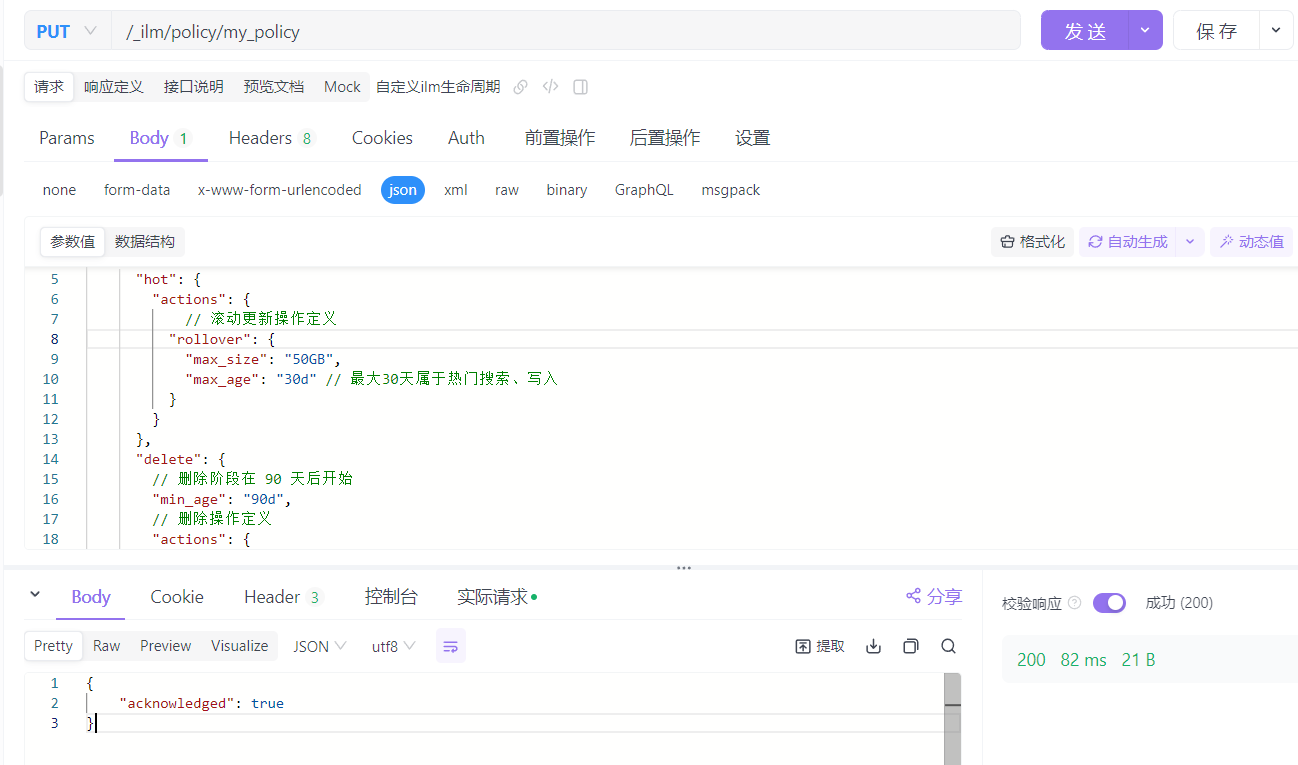
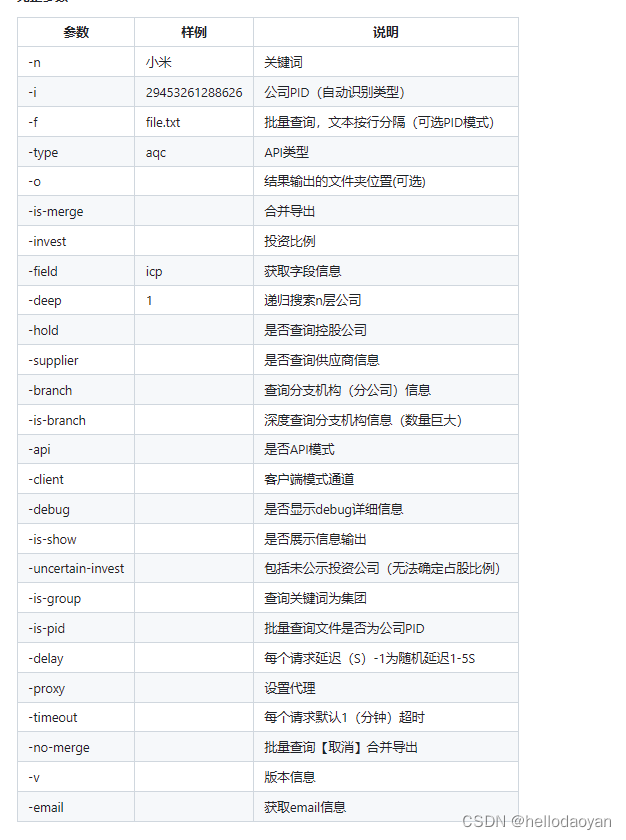
xt是我院19级专业第一,但他认为保研并不能展示他全部的实力,所以他在22年初试一结束就加入了23考研的队伍中,并且他为了填补我院近些年来无北大研究生的空白,毅然决然决定扛起19级的大旗,在学校百年华诞之际献上他最诚挚的礼物。
xt每天都游走在寝室,食堂和图书馆,三点一线,即便是在疫情局势蔓延的形势下,凌晨三点半刚做完核酸,他六点半还是照常起来卷。现在他太忙了,好像在提前准备复试了,想让你帮个小忙,xt会给出学校的地图(有向图),并且给出寝室,食堂和图书馆的编号(编号从0开始),希望你从该图中找出一个子图,要使得在这个子图中,寝室能够到达图书馆,食堂也能到达图书馆,同时希望在这个子图中的所有边的边权之和最小。如果你找不到任何一个子图符合要求的话(),输出“xt,我好没本领!”,因为你找不到并不代表xt找不到
子图的定义:
从原图中删去一些点或删去一些线或既删去一些点又删去一些线,剩下的部分(当然必须仍然是图)。允许两种极端情况:什么都不删;删去所有点和所有线。
输入格式:
第一行输入点的个数 n,3 <= n <= 105,边的个数 m,0 <= m <= 2∗105
第二行给出寝室的编号id1,食堂的编号id2,图书馆的编号id3,题目保证三个编号两两不同。
随后 m 行按照以下形式描述边,表示有一条有向边,起点是from,终点是to,权值是w
from to w
0 <= from, to <= n - 1,from != to,1 <= w <= 109
输出格式1:
如果子图存在则输出最小边权和,如果不存在输出“xt,我好没本领!”
输入样例1:
6 9
0 1 5
0 2 2
0 5 6
1 0 3
1 4 5
2 1 1
2 3 3
2 3 4
3 4 2
4 5 1
输出样例1:
9
解释:
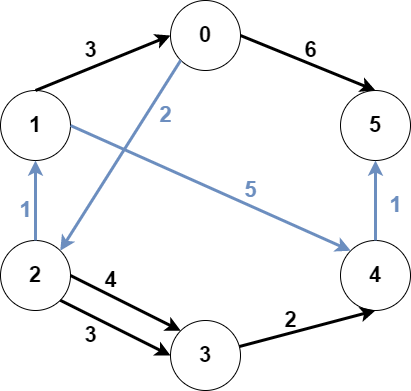
上图为输入的图。
蓝色边为最优子图之一。
注意,直接选择0 1 5三点构成的子图也能得到最优解,但无法在满足所有限制的前提下,得到更优解。
输入样例2:
3 2
0 1 2
0 1 1
2 1 1
输出样例2:
xt,我好没本领!
解释:

上图为输入的图。
可以看到,不存在从节点 1 到节点 2 的路径,所以不存在任何子图满足所有限制。
题目大意:
求寝室和食堂到图书馆的最短路。
思路:
跑三遍dijkstra,分别从寝室和食堂跑一边正向路,从图书馆跑一边反向路。
#include<bits/stdc++.h>
using namespace std;
typedef int ll;
#define endl "\n"
#define P pair<ll,ll>
const ll N = 1e5+7 ,M = 2e5+7 ,MAX = 0x3f3f3f3f3f3f3f3f/3;
ll n,m,now,nowf;//now为正向head初始点,nowf为反向head初始点
ll head[2][N],value[3][N],ne[2][M],e[2][M],v[2][M];//0记录反向路,1记录正向路
void add(ll x ,ll y ,ll z ,bool f){//用f判断路的方向
if(f)e[1][now] = y ,ne[1][now] = head[1][x] ,v[1][now] = z ,head[1][x] = now++;
else e[0][nowf]= y ,ne[0][nowf]= head[0][x] ,v[0][nowf]= z ,head[0][x] = nowf++;
}
void dj(ll x ,ll y ,ll z){
priority_queue<P,vector<P>,greater<P> >q;
q.push({0,x});
value[y][x]=0;
while(!q.empty()){
ll op = q.top().second;
q.pop();
for(ll i = head[z][op] ; ~i ; i = ne[z][i]){
ll to = e[z][i] ,va = v[z][i];
if(value[y][to] > value[y][op] + va){
value[y][to] = value[y][op] + va;
q.push({value[y][to],to});
}
}
}
return;
}
void solve(){
memset(head,-1,sizeof head);
memset(value,MAX,sizeof value);
ll x,y,z,id1,id2,id3,mx=MAX;now=0,nowf=0;
cin >> n >> m >> id1 >> id2 >> id3;
while(m--){
cin >> x >> y >> z;
add(x,y,z,1),add(y,x,z,0);
}
dj(id1,1,1),dj(id2,2,1),dj(id3,0,0);
for(ll i = 0 ; i < n ; i ++)
mx = min(mx , value[0][i] + value[2][i] + value[1][i]);
mx < MAX ? cout << mx << endl : cout << "xt,我好没本领!"<< endl;
return;
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
ll t=1;//cin >> t;
while(t --)solve();
return 0;
}