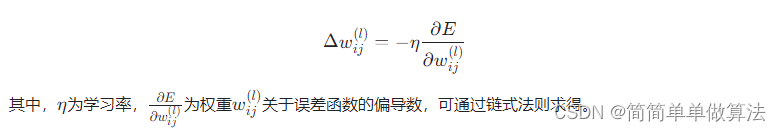一和零
力扣原题
给定一个二进制字符串数组 strs 和两个整数 m 和 n,请你找出并返回 strs 的最大子集的长度,该子集中最多有 m 个 0 和 n 个 1。
示例 1:
输入:strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ,因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = [“10”, “0”, “1”], m = 1, n = 1
输出:2
解释:最大的子集是 {“0”, “1”} ,所以答案是 2 。
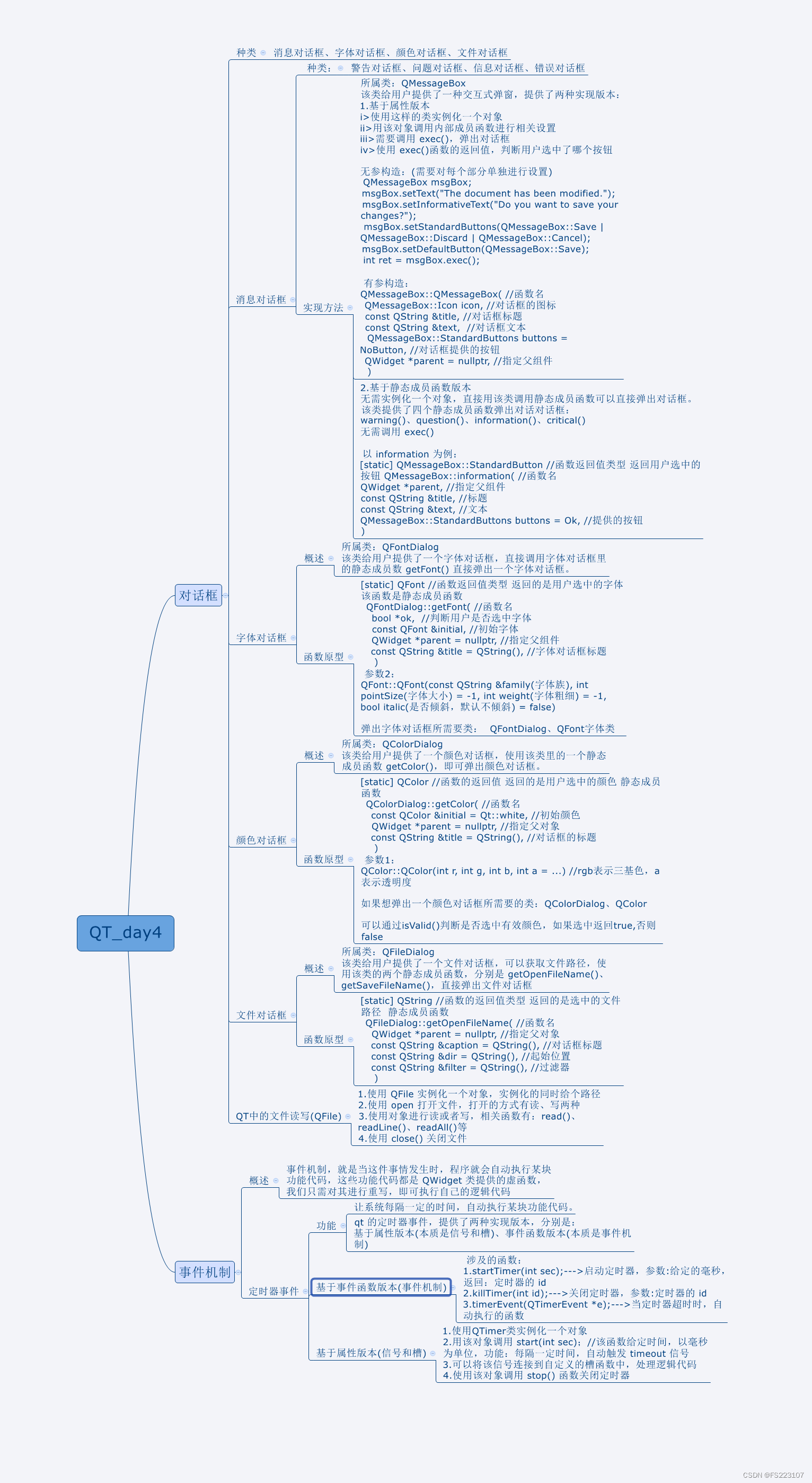
二维数组解法

分析
这是一个典型的二维动态规划问题。我们可以将每个字符串看作是一种物品,其中 0 的个数和 1 的个数就是物品的体积和价值。题目要求最大子集的长度,相当于要求装入背包的物品数量的最大值,而背包的容量由给定的 m 和 n 决定。
状态定义
我们定义一个二维的动态规划数组 dp,其中 dp[i][j] 表示在前 i 个字符串中,能够拥有不超过 m 个 0 和不超过 n 个 1 的最大子集的长度。
状态转移方程 (二维背包问题,实质上还是01背包,因为“物品”只能选一次)
在状态转移方程中,我们需要考虑当前字符串是否放入背包中的两种情况:
- 如果不放入当前字符串,则
dp[i][j] = dp[i-1][j]; - 如果放入当前字符串,则
dp[i][j] = dp[i-1][j-当前字符串中0的个数][j-当前字符串中1的个数] + 1。
综合以上两种情况,状态转移方程为:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-当前字符串中0的个数][j-当前字符串中1的个数] + 1)
初始化
我们需要对动态规划数组进行初始化,当没有字符串时或背包容量为0时。
Java解题
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp = new int[m + 1][n + 1]; // 初始化动态规划数组
for (String str : strs) { // 遍历物品,每个物品(每个字符串)只能使用一次,相当于01背包
int zeros = 0, ones = 0; // 每次循环都初始化 统计当前字符串中0和1的个数
for (char c : str.toCharArray()) {
if (c == '0') zeros++;//计算“0物品”的重量
else ones++;//计算“1物品”的重量
}
//遍历背包,相当于背包有两个维度
for (int i = m; i >= zeros; i--) { // 更新动态规划数组
for (int j = n; j >= ones; j--) {
dp[i][j] = Math.max(dp[i][j], dp[i - zeros][j - ones] + 1);
}
}
}
return dp[m][n]; // 返回最大子集的长度
}
}
总结
通过以上步骤,我们可以解决这个问题。首先将每个字符串看作是一种物品,然后根据动态规划的思想进行状态转移,最终返回最大子集的长度。
三维数组解法

分析
这是一个典型的动态规划问题。我们需要在满足条件的情况下找出最大子集的长度。可以将问题转化为01背包问题,其中背包的容量为 (m, n),物品的重量和价值分别为字符串中 0 和 1 的数量。
状态定义
定义一个三维动态规划数组 dp,其中 dp[i][j][k] 表示在前 i 个字符串中,最多有 j 个 0 和 k 个 1 的最大子集的长度。
状态转移方程
对于每一个字符串 strs[i],我们有两种选择:选择或者不选择。因此状态转移方程为:
dp[i][j][k] = max(dp[i - 1][j][k], dp[i - 1][j - zero][k - one] + 1)
其中 zero 和 one 分别表示字符串 strs[i] 中 0 和 1 的数量。
初始化
我们需要对动态规划数组进行初始化。初始时,前 0 个字符串中最多有 0 个 0 和 0 个 1 的最大子集的长度为 0。
Java解题
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][][] dp = new int[strs.length + 1][m + 1][n + 1];
for (int i = 1; i <= strs.length; i++) {
int[] count = countZeroesOnes(strs[i - 1]);
int zeros = count[0], ones = count[1];
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; k++) {
dp[i][j][k] = dp[i - 1][j][k];
if (j >= zeros && k >= ones) {
dp[i][j][k] = Math.max(dp[i][j][k], dp[i - 1][j - zeros][k - ones] + 1);
}
}
}
}
return dp[strs.length][m][n];
}
private int[] countZeroesOnes(String str) {
int[] count = new int[2];
for (char c : str.toCharArray()) {
count[c - '0']++;
}
return count;
}
}
总结
通过动态规划的思想,我们可以解决这个问题。首先计算每个字符串中 0 和 1 的数量,然后根据状态转移方程进行状态转移,最终返回最大子集的长度。